SLAM中的非线性优化

　　总结一下SLAM中关于非线性优化的知识。

先列出参考：

http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/

http://blog.csdn.net/dsbatigol/article/details/12448627

http://www.cnblogs.com/rongyilin/archive/2012/12/21/2827898.html

《视觉SLAM十四讲》。

1. 雅克比矩阵 && 海森矩阵

　　雅克比矩阵（Jacobian）是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅克比行列式。它体现了一个可微方程与给出点的最优线性逼近，类似与多元函数的导数。

　　假设F：R_n→R_m是一个从欧式n维空间转换到欧式m维空间的函数，这个函数由m个实函数组成：u₁（x₁，...，x_n），...，u_m（x₁，...，x_n）。假设这些函数的偏导数存在，则雅克比矩阵可以写成：

　　海森矩阵（Hessian）是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵，设函数为：f（x₁，x₂，...，x_n），并假设f的二阶导数粗在，则其海森矩阵为：

　　海森矩阵常被应用于牛顿法解决大规模的优化问题，具体可参考：http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/。

2.最小二乘问题

　　最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。

2.1 线性最小二乘

　　已知M个N+1维空间点：

，

其中，

。

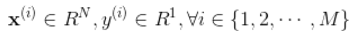如何求的函数f(x)：

。

可以构建最小二乘问题估计f(x)的参数：

，

写成矩阵形式为：

，

其中：

为了最小化上式，对w求导，并另导数等于0：

。

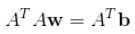上式的获取需要先展开平方项，然后进行矩阵的求导。只要求出w矩阵就可以了，一般线性最小二乘需要用到Cholesky的分解，具体的求解过程就不展开了。

2.2 非线性最小的二乘

　　非线性最小二乘指的是f(x)函数是一个非线性函数，导致导数的求解变的非常困难，因此需要求解非线性最小二乘问题的方法。而求解方法中就包括最速下降法，牛顿法，高斯-牛顿法(G-N)，列文伯格-马夸尔特法(L-M)等，它们都是通过迭代的方式逼近最优解，下面分别做一个简单的介绍。

3. 1最速下降法

　　它的思想是每次迭代选取一个步长λ，根据函数的梯度选择下降最快的方向，使得目标函数的值能够最大程度的下降。这里主要是理解算法思想，具体的算法操作还应该查阅相关书籍。我们假设f(x)是一个待优化的函数（其实对于最小二乘来说，它应该是一个残差函数，有的地方也叫cost founction）:min1/2||f(x)||²，对其进行一阶泰勒展开：

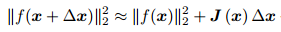
其中的J(x)为雅克比矩阵，即函数平方关于x的导数，根据上式可以求取增量和步长λ，然后进入迭代循环。但是该方法收敛速度比较慢，直接使用最速下降法效果不好。

3.2 牛顿法

　　牛顿法相比最速下降法更进一步，对待优化函数进行二阶泰勒展开：

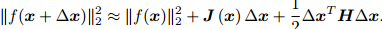
则增量为：

它是一个关于雅克比矩阵和海森矩阵的问题，所以计算量稍大。

3.3 高斯-牛顿法

　　可以看到上面的方法都是对残差函数的平方项直接进行泰勒展开，而高斯牛顿法则是对f(x)进行泰勒展开，然后对展开项进行平方和：

由于每次迭代都需要求解一个增量，现在可以构建关于增量的线性最小二乘问题：

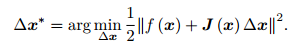
因此只要对上式求导，并另导数为0，就能求解增量：

通常上式都写成如下形式：

获得这个增量方程，需要对上面的线性最小二乘问题进行矩阵的平方项计算以及相应的矩阵求导，其实这和前面说过的非线性最小二乘问题本质上是一样的，获得的数学结论也类似，但是关于上式的求解方法在SLAM系统里跟线性方法不太一样。

3.4 列文伯格-马夸尔特法

　　L-M法是对高斯牛顿法的一个改进，给增量添加一个信赖区域：

分子是实际函数的下降值，分母是近似模型的下降值（分母的问题可以回忆一下微积分）。上式太小，说明实际下降值小于近视下降值，所以你的估计下降的太快了；如果上式太大，说明实际下降值大于近似下降值，所以你可以快点下降没关系。这样，高斯牛顿法的最小二乘问题变成：

用拉格朗日乘数法就是：

同样进行平方项的展开以及对增量的求导：

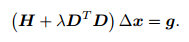
这就是L-M中的增量方程。