一本通 P1486 【黑暗城堡】

• 题库 ：一本通
• 题号 ：1486
• 题目 ：黑暗城堡
• link ：http://ybt.ssoier.cn:8088/problem_show.php?pid=1486

---

思路 ：这道题既然要求使加入生成树中的点到1号节点的距离最小，那么我们可以理解为题目要求一个最短路径生成树，那么我们可以从1号节点向每个节点跑一遍SPFA最短路，并记录下来。这道题中如果满足两个点i，j && dis[i] = dis[j] + f[i][j]（dis[i]表示第i个点到1号节点的最短距离，f[i][j]表示i向j连的直接路径的长度）那么就满足题目中的条件（生成树中的某个点到1号节点的路径等于从当前点到1号节点的最短路径），所以当前点的答案数++，最后再用乘法原理把他们的方案数乘起来。

证明一下为什么 dis[i] = dis[j] + f[i][j] 答案数就++ ：

如样例图所示：

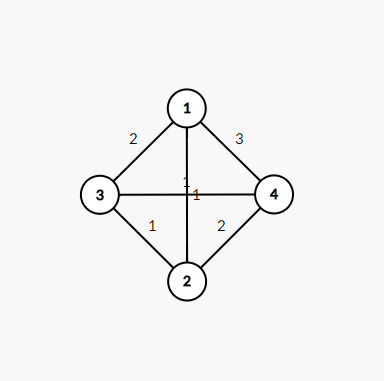
我们手动模拟求得dis[1] = 0, dis[2] = 1, dis[3] = 2,  dis[4] = 3（f的就不求了）

开始模拟：

• 第2号节点 ：枚举所有点，显而易见只有dis[2] = dis[1] + f[2][1]的这种情况（每个节点都会有这种情况的，即直接走最短路）
• 第3号节点 ：枚举所有点，显而易见有两种情况，一是直接走最短路（这里就不写了），二是经过2号节点，再到达1号节点dis[3] = dis[2] + f[3][2]
• 第4号节点 ：枚举所有点，显而易见有三种情况，一是直接走最短路（这里就不写了），二是经过2号节点，再到达1号节点dis[4] = dis[2] + f[4][2]，三是经过3号节点，再到达1号节点dis[4] = dis[3] + f[4][3]

综上所述，如果一个节点可以经过另一个节点到达1号节点，而且距离还是相同的，那么答案数就可以++了。这里采用了Floyed的思想

那个式子翻译成中文就是如果一个节点到1号节点的最短路 = 另一个和它有连边的节点到根节点的最短路 + 它们两个节点之间的直接距离，那么答案数++，而那条边要不然就是在最短路里，要不然就是另一种方案

code ：

 #include <bits/stdc++.h>
 #define INF 0x3f3f3f3f
 using namespace std;
 const long long MOD = pow(, ) - ;//别忘了取膜
 int n, m, x, y, num, head[], vis[];
 long long ans, z, dis[], f[][];//这些变量最好开long long
 struct node
 {
     int next, to;
     long long val;
 }stu[];
 inline void add(int x, int y, int z)//标准链式向前星
 {
     stu[++num].next = head[x];
     stu[num].to = y;
     stu[num].val = z;
     head[x] = num;
     return;
 }
 inline void spfa(int s)//SPFA最短路
 {
     memset(vis, , sizeof(vis));
     memset(dis, INF, sizeof(dis));
     queue < int > pru;
     pru.push(s);
     dis[s] = ;
     vis[s] = ;
     while(!pru.empty())
     {
         int u = pru.front();
         pru.pop();
         vis[u] = ;
         for(register int i = head[u]; i; i = stu[i].next)
         {
             int k = stu[i].to;
             if(dis[k] > dis[u] + stu[i].val)
             {
                 dis[k] = dis[u] + stu[i].val;
                 if(!vis[k])
                 {
                     vis[k] = ;
                     pru.push(k);
                 }
             }
         }
     }
     return;
 }
 int main()
 {
     memset(f, INF, sizeof(f));//初始化
     scanf("%d %d", &n, &m);
     for(register int i = ; i <= m; ++i)
     {
         scanf("%d %d %lld", &x, &y, &z);
         add(x, y, z);//无向图
         add(y, x, z);
         f[x][y] = f[y][x] = min(f[x][y], z);//取最小(不知道有没有毒瘤数据)
     }
     spfa();//从1号节点出发
     ans = ;//初始化为1
     for(register int i = ; i <= n; ++i)//1号节点不算
     {
         int sum = ;//当前节点的方案数
         for(register int j = ; j <= n; ++j)//枚举
         {
             if(dis[i] == dis[j] + f[i][j])//不解释
             {
                 ++sum;
             }
         }
         if(sum)//这里其实不需要特判，因为每个点都一定会有走最短路这种情况
         {
             ans = ans * sum % MOD;//乘法原理 + 边乘边膜
         }
     }
     printf("%lld", ans);
     return ;
 }