poj 2991 起重机

地址 http://poj.org/problem?id=2991

题解

本来以为这是一个简单的线段树模板 不料始终不太明白线段树如何记录转动角度后的各个线段端的XY值

学习了网络上的一些博客题解 感觉似是而非 谈到复数 角度 向量等，有点不太好理解

现在这里将自己的理解记录如下

如图

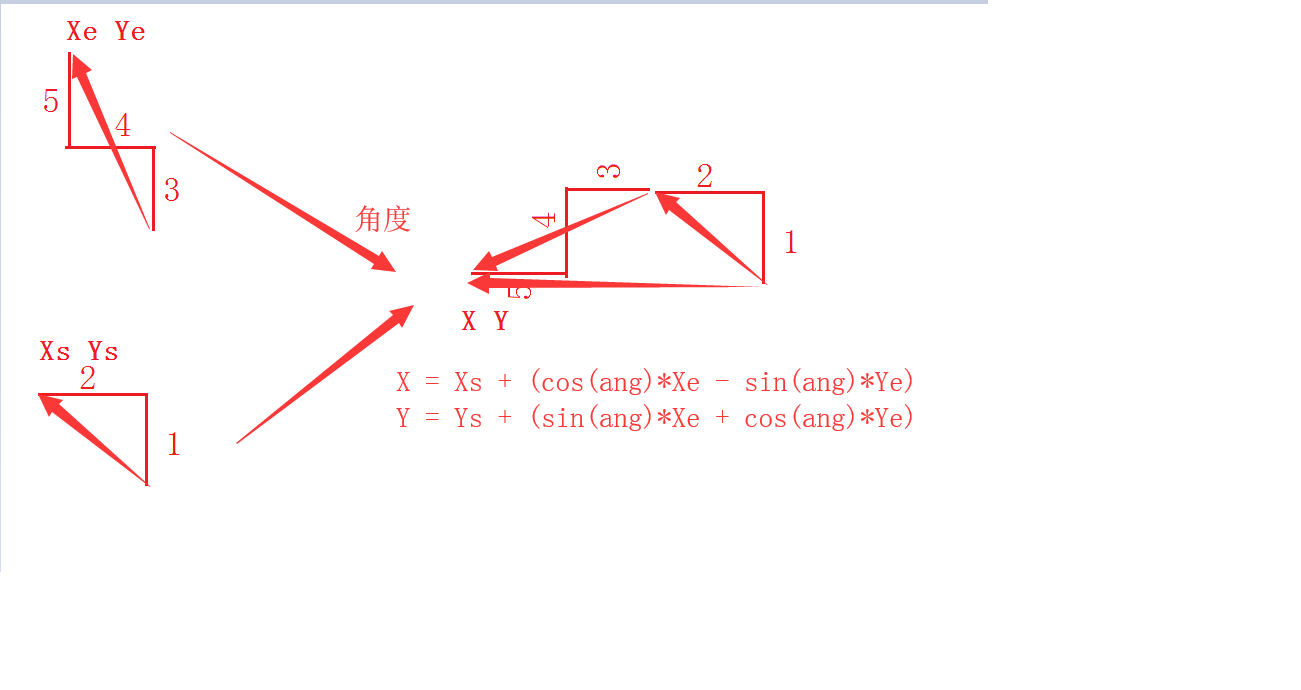
1 预备知识

使用线段树记录的内容如下  指示某段线段的组合 以第一条线段为垂直 最后的线段的端点的X Y值

途中1~2 线段 和3~5线段 就是线段树节点1~5的子节点 那么线段树节点1~5 就记录1~5结合后的X Y 值以及两个子节点结合的角度值

由于3~5线段的XY 是以自己的第一条线段为垂直起点为0 0 计算出来的X Y

那么在于1~2线段合并的时候 并不是简单的将两子节点的X Y相加即可得到1~5线段的XY 而是要加入旋转了相对角度 该角度由记录1~5线段的线段树节点记录

1~2线段部分的X Y值 旋转相对角度的公式推导如下

https://blog.csdn.net/hjq376247328/article/details/45113563

其实也就是

xNew = x * cosB - y * sinB

yNew = x * sinB + y * cosB

再来和 1~2线段的X Y相加即可得到1~5线段的X Y，并将该两子节点的相对角度记录在父节点中

预备知识讲完

2 解答步骤如下

一  建造线段树 build(1,1,n); 由于每条线段都是垂直连接 所以X 均为0 相对角度全部为0

void build(int k,int l,int r) {
    angT[k]=x[k]=0.0;
    if(r==l) y[k]=L[l];
    else {
        int lson=k*, rson=k*+;
        int m=(l+r)/;
        build(lson,l,m);
        build(rson,m+,r);
        y[k]=y[lson]+y[rson];
    }
}

二 某段线段转动角度后

题意输入的角度是si和si+1逆时针角度而不是旋转的角度，而是需要转到的结果角度， 所以我们需要进行转换 。所以使用了pre数组记录每段线段与相邻线段的逆时针间隔角度，这样接收到题意输入角度a后

a-pre[s] 就是实际要转动的角度 而且需要更新pre[s] 以便下次计算

change(s,ang-pre[s],,,n);
pre[s]=ang; // 要求改变为a度 考虑之前已改变过

chang()代码就是批量更新需要转换的角度和X Y

只有旋转的起点线段在当前线段树节点的左子节点 我们才更新当前线段树节点的角度记录

如图

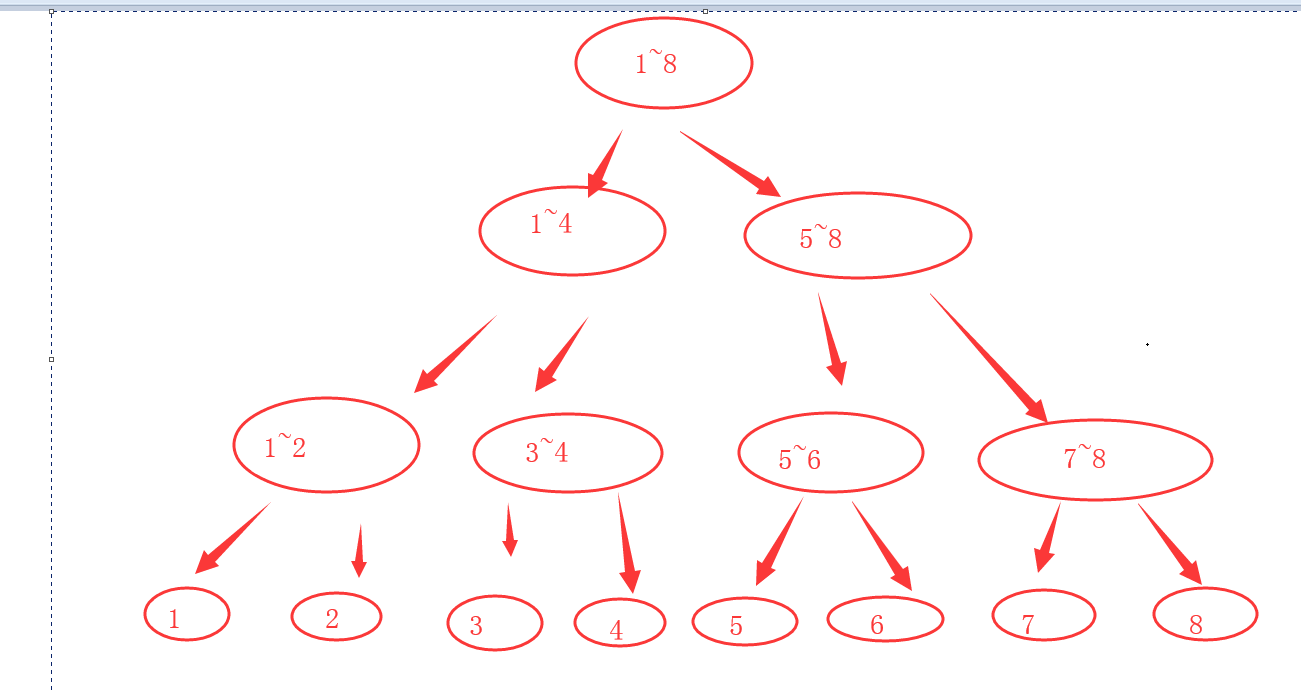
假设节点4 向3旋转90度

那么合并1 2的时候无更新

合并3 4的时候 3~4节点的角度要在原来记录上再旋转90

合并1~2 3~4为1~4的时候无需更新角度 因为 3~4 已经旋转 与1 ~2的相对角度 并没有变化

同样 5~8节点流程中无变化

但是合并1~4 5~8节点的时候 角度需要旋转90

整个流程下来  4 5~8 角度均旋转更新1次  符合题目的集合意义

最后返回1~8节点记录的X Y即可

代码如下

 #include <iostream>
 #include <vector>
 #include <math.h>
 #include <stdio.h>
 using namespace std;
 const double PI = acos(-1.0);
 const int N = ;

 int n, c, L[N];
 double pre[N];

 double angT[N << ];
 double x[N << ], y[N << ];

 void build(int k, int l, int r) {
     angT[k] = x[k] = 0.0;
     if (r == l) y[k] = L[l];
     else {
         int lson = k * , rson = k *  + ;
         int m = (l + r) / ;
         build(lson, l, m);
         build(rson, m + , r);
         y[k] = y[lson] + y[rson];
     }
 }

 void change(int s, double ang, int k, int l, int r) {
     if (s < l || l == r) return; // 操作位置不在范围内 或 区间长度为1 不作处理
     else if (s <= r) {
         int lson = k * , rson = k *  + ;
         int m = (l + r) / ;
         change(s, ang, lson, l, m);
         change(s, ang, rson, m + , r); // 先处理左右子区间
         if (s <= m) angT[k] += ang; // 操作位置位于区间的左子区间内 可根据左右子区间的向量更新

         double sina = sin(angT[k]), cosa = cos(angT[k]);
         x[k] = x[lson] + (x[rson] * cosa - y[rson] * sina);
         y[k] = y[lson] + (x[rson] * sina + y[rson] * cosa);
     }
 }

 /*
 Sample Input

 2 1
 10 5
 1 90

 3 2
 5 5 5
 1 270
 2 90
 Sample Output

 5.00 10.00

 -10.00 5.00
 -5.00 10.00
 */

 int main()
 {
     while (~scanf("%d%d", &n, &c)) {
         for (int i = ; i <= n; i++) {
             scanf("%d", &L[i]);
             pre[i] = PI;
         }
         build(, , n);
         while (c--) {
             int s, a; scanf("%d%d", &s, &a);
             double ang = (double)a / 180.0*PI;
             change(s, ang - pre[s], , , n);
             pre[s] = ang;
             printf("%.2f %.2f\n", x[], y[]);
         }
         printf("\n");
     }

     return ;
 }