多维标度法（MDS）的Python实现

多维标度法(multidimensional scaling，MDS)是一种在低维空间展示“距离”数据结构的多元数据分析技术,是一种将多维空间的研究对象( 样本 或 变量 ) 简化到低维空间进行定位、分析和归类， 同时又保留对象间原始关系的数据分析方法。

多维标度法与主成分分析(Principle Component Analysis，PCA)、线性判别分析(Linear Discriminent Analysis，LDA)类似，都可以用来降维.(注：在PCA中，我们降维所用的方法依次寻找正交的并且variance最大的方向，因为variance能够最大程度的保存原特征空间中的信息。在LDA中，因为数据有label，通过一个线性变换，把每个类的中心点 M_k映射到一个新的空间，使得在这个新的空间上，一方面各个中心点之间的距离（这里可称之为类间距离）尽量保持足够大，另一方面每个类里面的点到其中心点的距离（这里可称之为类内距离）尽量小。更多细节略)

多维标度法的目标：当n 个对象中各对对象之间的相似性（或距离）给定时，确定这些对象在低维(欧式) 空间中的表示（称为感知图, Perceptual Mapping），并使其尽可能与原先的相似性（或距离）“大体匹配”，使得由降维所引起的任何变形达到最小。

低维(欧式) 空间中排列的每一个点代表一个对象，因此点间的距离与对象间的相似性高度相关。也就是说，两个相似的对象由低维(欧式) 空间中两个距离相近的点表示，而两个不相似的对象则由低维(欧式) 空间两个距离较远的点表示。低维空间通常为二维或三维的欧氏空间，但也可以是非欧氏三维以上空间.

Classical MDS:

• 原始空间下的距离阵和低维空间下的距离阵都采用欧式距离阵
• 距离阵D 为欧式的, 即存在某个正整数p 以及R^p 空间的n个点x₁, . . . , x_n, 使得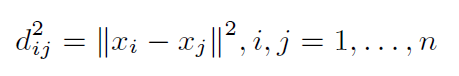

目标在于: 寻找D 的(拟合) 构图x₁, . . . , x_n, 其想法为
– 将平方的欧式距离阵D = (d²_ij) 变换为一个非负定矩阵B
– 由B 的特征根和特征向量得到构图X, X 的每一行表示低维空间的点.
• 为此, 记原始的p 维对象(观测点) 为x₁, . . . , x_n(一般是未知的), 两两之间的距离平方为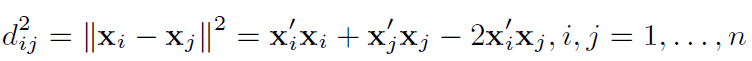

B = −1/2*HDH,H = In − 1/n 11′

其中, r 的确定: 事先确定r = 1, 2 或3; 或者通过计算前面特征根占全体特征根的比例确定.

import numpy as np

D=np.array([[0,411,213,219,296,397],
            [411,0,204,203,120,152],
            [213,204,0,73,136,245],
            [219,203,73,0,90,191],
            [296,120,136,90,0,109],
            [ 397,152,245,191,109,0]])

N = D.shape[0]
T = np.zeros((N,N))

#solution 1
#ss = 1.0/N**2*np.sum(D**2)
#for i in range(N):
#    for j in range(i,N):
#        T[i,j] = T[j,i] = -0.5*(D[i,j]**2 -1.0/N*np.dot(D[i,:],D[i,:]) -1.0/N*np.dot(D[:,j],D[:,j])+ss)

#solution 2
#K = np.dot(D,np.transpose(D))
D2 = D**2
H = np.eye(N) - 1/N
T = -0.5*np.dot(np.dot(H,D2),H)

eigVal,eigVec = np.linalg.eig(T)
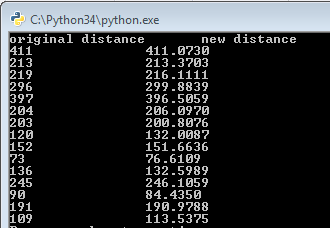
X = np.dot(eigVec[:,:2],np.diag(np.sqrt(eigVal[:2]))) 

print('original distance','\tnew distance')
for i in range(N):
    for j in range(i+1,N):
        print(np.str(D[i,j]),'\t\t',np.str("%.4f"%np.linalg.norm(X[i]-X[j])))

运行结果：

参考文档：典型相关分析和多维标度法-张伟平的讲义