[Agc011F] Train Service Planning

题目大意：

有n+1个车站，n条轨道，第i条轨道联通i-1和i车站，通过它要花a[i]时间，这条轨道有b[i]=1或2条车道，也就是说，他是单向还是双向的。

要满足以下约定

所有的火车要么从站台0到站台n，要么从站台n到站台0
对任意终点为n的火车，如果它在t时刻离开站台i−1并开往站台i，那么它必须在t+Ai时刻到达i站台，对反方向要求相同
对任意终点为n的火车，如果它在s时刻到达站台i并在t时刻离开站台i，那么下一列经过站台i的终点为n的火车必须在s+K时刻到达站台i并在t+K时刻离开站台i，对反方向要求相同![]
在任意时刻不能有两列相向而行的火车在单向区间内互相穿过

要求最小化两种火车从起点到终点的时间和。

$n\leq 10^5,a_i\leq 10^9$

试题分析

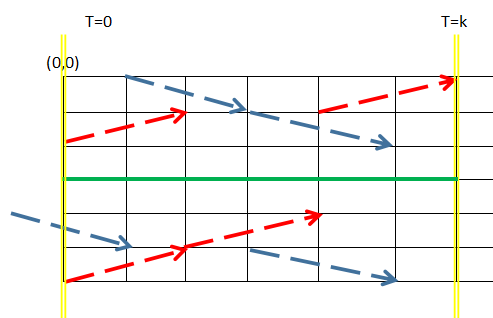
不难发现，双向道路上如果有两条线（列车行驶）的交是没有问题的，因为可以双向行驶。

但是单向的话就不行了，需要在某个车站进行等待并交换道路。

然而我们需要求这些车的行驶时间的和，怎么办呢？

一个非常重要的传统办法——列式子。

我们下面把第一辆车称作1号，把第二辆（$n\to 0$）称作2号。

设$q_i$为1号每站的等待时间，$p_i$为2号每站的等待时间。

于是有：$tim_1=\sum_{i=0}^{n-1} q_i+a_i,tim_2=\sum_{i=0}^{n-1} p_i+a_i$

那么走到其中一个点$j$的时间是多少呢？

\[tim_{1,j}=\sum_{i=0}^{j-1} q_i+a_i
\]

\[tim_{2,j}=\sum_{i=0}^{j-1} p_i+a_i
\]

还是没有突破口，继续列式子。。。

发现1号走过$j-1\to j$的时间区间是$(\sum_{i=0}^{j-2} q_i+a_i +q_{j-1},\sum_{i=0}^{j-1} q_i+a_i)$

2号同理。

这个东西乍一看没有办法搞，但是这道题有一个很重要的性质：时间K就是一个循环节。

那么我们就可以把这个东西丢到$\pmod{k}$的意义下去做。

既然图上的线不交，就意味着1号和2号的站中间的时间区间不交。

于是继续列出限制条件，然后移项变换，得到：$$\sum_{i=0}^{j}(p[i]+q[i])\not \in[-2s[j],-2(s[j]-a[j])]$$

其中$s$为$a$的前缀和。

那么问题就变成了：

有一个人，在数轴上走，从左到右每次向右走（可以不走），每次走的地方在$[l_i,r_i]$中，问代价。

因为是$\pmod{k}$意义下，所以可以把两段补区间前后相接得到一个新的区间。

能在原地踏步显然在原地踏步，所以我们需要找的是$[l_j,r_j]$不包含$l_i$的$j>i$的区间。

这个东西我们可以线段树的区间覆盖加上贪心dp出来。

#include<iostream>

#include<cstring>

#include<cstdio>

#include<vector>

#include<algorithm>

//#include<ctime>

//#include<cmath>

//#include<queue>

using namespace std;

#define LL long long

inline int read(){

    int x=0,f=1; char c=getchar();

    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;

    for(;isdigit(c);c=getchar()) x=x*10+c-'0';

    return x*f;

}

const LL INF = 2147483600;

const LL MAXN = 300010;

LL N,K;

LL tag[MAXN<<2],col[MAXN<<2];

inline void tage_lazy(LL rt){

    if(tag[rt]){

        col[rt<<1]=tag[rt]; col[rt<<1|1]=tag[rt];

        tag[rt<<1]=tag[rt]; tag[rt<<1|1]=tag[rt];

        tag[rt]=0;

    }

}

inline void Cover(LL rt,LL l,LL r,LL L,LL R,LL k){

    if(L>R) return ;

    if(L<=l&&R>=r){tag[rt]=k; col[rt]=k; return ;} tage_lazy(rt);

    LL mid=(l+r)>>1; if(L<=mid) Cover(rt<<1,l,mid,L,R,k);

    if(R>mid) Cover(rt<<1|1,mid+1,r,L,R,k); return ;

}

inline LL Query(LL rt,LL l,LL r,LL k){

    if(l==r) return col[rt]; LL mid=(l+r)>>1; tage_lazy(rt);

    if(k<=mid) return Query(rt<<1,l,mid,k);

    else return Query(rt<<1|1,mid+1,r,k);

}

LL f[MAXN+1],Num[MAXN<<1];

LL l[MAXN+1],r[MAXN+1],tot;

inline LL Ask(LL k){

    LL pos=Query(1,1,tot,k);

    return (pos?f[pos]+(Num[l[pos]]-Num[k]+K)%K:0);

}

LL a[MAXN+1],b[MAXN+1],s[MAXN+1];

int main(){

    //freopen(".in","r",stdin);

    //freopen(".out","w",stdout);

    N=read(),K=read(); tot=0;

    for(LL i=1;i<=N;i++){

        a[i]=read(),b[i]=read();

        s[i]=(s[i-1]+a[i]);

        if(b[i]==2){l[i]=0; r[i]=K-1;}

        else l[i]=(K-2*s[i-1]%K)%K,r[i]=(K-2*s[i]%K)%K;

        if(b[i]==1&&a[i]*2LL>K){puts("-1"); return 0;}

        Num[++tot]=l[i]; Num[++tot]=r[i];

        //cout<<"x:"<<l[i]<<" "<<r[i]<<endl;

    } sort(Num+1,Num+tot+1); tot=unique(Num+1,Num+tot+1)-Num-1;

    for(LL i=1;i<=N;i++){

        l[i]=lower_bound(Num+1,Num+tot+1,l[i])-Num;

        r[i]=lower_bound(Num+1,Num+tot+1,r[i])-Num;

    } for(LL i=N;i>=1;i--){

        f[i]=Ask(l[i]);

        if(l[i]>r[i]) Cover(1,1,tot,r[i]+1,l[i]-1,i);

        else Cover(1,1,tot,1,l[i]-1,i),Cover(1,1,tot,r[i]+1,tot,i);

    } LL ans=f[1];

    for(LL i=tot;i>=1;i--) ans=min(ans,Ask(i));//cout<<i<<": "<<Ask(i)<<endl;

    printf("%lld\n",ans+2LL*s[N]);

    return 0;

}