决策树算法（C4.5）

ID3具有一定的局限性，即信息增益倾向于选择取值比较多的特征(特征越多，条件熵(特征划分后的类别变量的熵)越小，信息增量就越大)，C4.5通过选择最大的信息增益率 gain ratio 来选择节点可以解决该问题。并且C4.5算法可以处理连续和有缺失值的数据。

C4.5与ID3在实现过程中，不同之处在于将计算信息增益的函数改为计算信息增益率。

譬如，对于上一个例子中的湿度这一项的取值改为：

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	85	Weak	No
2	Sunny	Hot	90	Strong	No
3	Overcast	Hot	78	Weak	Yes
4	Rain	Mild	96	Weak	Yes
5	Rain	Cool	80	Weak	Yes
6	Rain	Cool	70	Strong	No
7	Overcast	Cool	65	Strong	Yes
8	Sunny	Mild	95	Weak	No
9	Sunny	Cool	70	Weak	Yes
10	Rain	Mild	80	Weak	Yes
11	Sunny	Mild	70	Strong	Yes
12	Overcast	Mild	90	Strong	Yes
13	Overcast	Hot	75	Weak	Yes
14	Rain	Mild	80	Strong	No

Gain(Wind) = Entropy(S) – (8/14)* Entrogy(weak)-(6/14)* Entrogy(strong) = 0.048

weak = 8;Strong = 6

Feature(Wind) = -8/14*log(8/14)-6/14*log(6/14) = 0.9852

RatioGain(Wind) = Gain(Wind)/Feature (Wind) = 0.0487

同理：RatioGain(Outlook) = 0.247/1.577 = 0.1566

RatioGain(Temperature)= 0.029/1.556 = 0.018

其中，对于连续值的计算：

1.      对特征的取值进行升序排序

2.      两个特征取值之间的中点作为可能的分裂点，将数据集分成两部分，计算每个可能的分裂点的信息增益（InforGain）。优化算法就是只计算分类属性发生改变的那些特征取值。

3.      选择修正后信息增益(InforGain)最大的分裂点作为该特征的最佳分裂点

4.      计算最佳分裂点的信息增益率（Gain Ratio）作为特征的Gain Ratio。注意，此处需对最佳分裂点的信息增益进行修正：减去log2(N-1)/|D|（N是连续特征的取值个数，D是训练数据数目，此修正的原因在于：当离散属性和连续属性并存时，C4.5算法倾向于选择连续特征做最佳树分裂点）

故，划分为：{ 65、70、75、78、80、85、90、95、96 } 这几个特征。

	65		70		75		78		80		85		90		95		96
	≤	>	≤	>	≤	>	≤	>	≤	>	≤	>	≤	>	≤	>	≤	>
Yes	1	8	3	6	4	5	5	4	7	2	7	2	8	1	8	1	9	0
No	0	5	1	4	1	4	1	4	2	3	3	2	4	1	5	0	5	0
Entropy	0	0.961	0.811	0.971	0.722	0.991	0.65	1	0.764	0.971	0.881	1	0.918	1	0.961	0	0.94	0
Gain	0.048		0.015		0.045		0.090		0.102		0.025		0.011		0.048		0

此时，可以看到当特征小于等于80时，信息增益最大，选取该取值区间作为湿度属性的信息增益。

即Gain(Humidity) = 0.102

Feature(Humidity) = -9/14*log(9/14) - 5/14*log(5/14) = 0.940（两个分支，大于80的和小于等于80的）

RatioGain(Humidity) = 0.102/0.940 = 1.085

//------------------------------------------------

对于ID3算法局限性的理解：

X = [['sunny',    'hot',   'h_85',   'weak'],
     ['sunny',    'hot',   'h_90',   'strong'],
     ['overcast', 'hot',   'h_78',   'weak'],
     ['rain',     'mild',  'h_96',   'weak'],
     ['rain',     'cool',  'h_80', 'weak'],
     ['rain',     'cool',  'h_70', 'strong'],
     ['overcast', 'cool',  'h_65', 'strong'],
     ['sunny',    'mild',  'h_95',   'weak'],
     ['sunny',    'cool',  'h_70', 'weak'],
     ['rain',     'mild',  'h_80', 'weak'],
     ['sunny',    'mild',  'h_70', 'strong'],
     ['overcast', 'mild',  'h_90',   'strong'],
     ['overcast', 'hot',   'h_75', 'weak'],
     ['rain',     'mild',  'h_80',   'strong'],
]

　　对于ID3算法的输入改为，可以看到生成的决策树为：

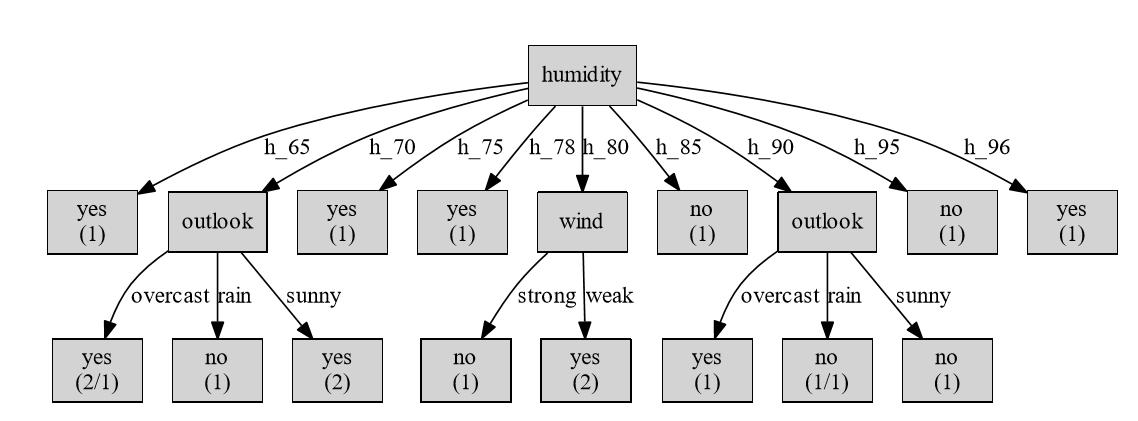
可以看到，此时就会出现过拟合的现象。

而采用信息增益率作为判决条件的话：

estimator = Id3Estimator(gain_ratio=1)

　　获得的决策树为：

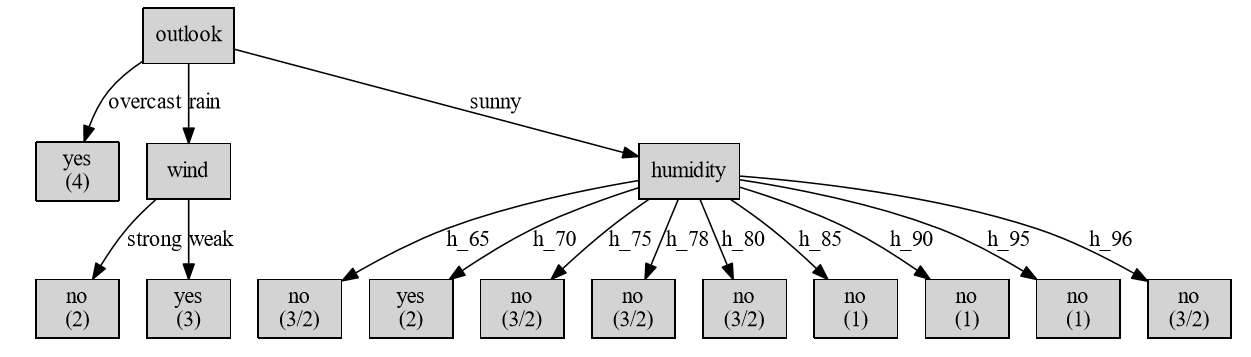
因此，对于使用信息增益作为分类准则和使用信息增益率的区别如上所示。

//-----------------------------------

对于处理数值的理解：

解读python的第三方库，ID3模块（decision-tree-id3）

在其中id3.py模块中：

Id3Estimator类的fit函数中

for i in range(self.n_features):
            if check_input and check_numerical_array(X_[:, i]):
                self.is_numerical[i] = True
                X_tmp[:, i] = X_[:, i]
            else:
                X_tmp[:, i] = self.X_encoders[i].fit_transform(X_[:, i])

　　这里会判断一下传递的特征是名字还是数字，判断的方法在checks.py中：

def check_numerical_array(array):
    """ Check if all values in a 1d array are numerical. Raises error if array
        is more than 1d.

    Parameters
    ----------
    array : nparray
        containing the class names

    Returns
    -------
    result : bool
        True if all values in array are numerical, otherwise false
    """
    try:
        if array.ndim > 1:
            raise ArithmeticError("Found array with dim {}. Expected = 1."
                                  .format(array.ndim))
        array.astype(np.float64)
        return True
    except ValueError:
        return False

　　此处会做一个类型转换，如果输入的是数字、字符串形式的数字都会被转为float类型。

（此次我觉得不太妥当，字符串形式的数字不应该转化为数字，说不定人家就是想这样输入作为feature呢，譬如我上面的输入数字的开头还要加一个 ‘h_’）

当特征为数字的时候计算方法在splitter.py文件中：

def _info_numerical(self, x, y):
        """ Info for numerical feature feature_values
        sort values then find the best split value

        Parameters
        ----------
        x : np.array of shape [n remaining examples]
            containing feature values
        y : np.array of shape [n remaining examples]
            containing relevent class

        Returns
        -------
        : float
            information for remaining examples given feature
        : float
            pivot used set1 < pivot <= set2
        """
        n = x.size
        sorted_idx = np.argsort(x, kind='quicksort')
        sorted_y = np.take(y, sorted_idx, axis=0)
        sorted_x = np.take(x, sorted_idx, axis=0)
        min_info = float('inf')
        min_info_pivot = 0
        min_attribute_counts = np.empty(2)
        for i in range(1, n):
            if sorted_x[i - 1] != sorted_x[i]:
                tmp_info = i * self._entropy(sorted_y[0: i]) + \
                           (n - i) * self._entropy(sorted_y[i:])
                if tmp_info < min_info:
                    min_attribute_counts[SplitRecord.LESS] = i
                    min_attribute_counts[SplitRecord.GREATER] = n - i
                    min_info = tmp_info
                    min_info_pivot = (sorted_x[i - 1] + sorted_x[i]) / 2.0
        return CalcRecord(CalcRecord.NUM,
                          min_info * np.true_divide(1, n),
                          pivot=min_info_pivot,
                          attribute_counts=min_attribute_counts)

　　

可以看到，其计算过程和上述对于数值的计算过程一样，其min_info为选取的最小的分类后的信息熵，为了得到最大的信息增益。

而对于是否使用信息增益率的判断在splitter.py文件中：

def _is_better(self, calc_record1, calc_record2):
        """Compares CalcRecords using gain ratio if present otherwise
           using the  information.

        Parameters
        ----------
        calc_record1 : CalcRecord
        calc_record2 : CalcRecord

        Returns
        -------
        : bool
            if calc_record1 < calc_record2
        """
        if calc_record1 is None:
            return True
        if calc_record2 is None:
            return False
        if self.gain_ratio:
            if calc_record1.gain_ratio is None:
                calc_record1.gain_ratio = self._gain_ratio(calc_record1)
            if calc_record2.gain_ratio is None:
                calc_record2.gain_ratio = self._gain_ratio(calc_record2)
            if self._is_close(calc_record1.gain_ratio,
                              calc_record2.gain_ratio):
                return calc_record1.info > calc_record2.info
            else:
                return calc_record1.gain_ratio < calc_record2.gain_ratio
        else:
            return calc_record1.info > calc_record2.info

　　

故，对于C4.5算法，同样可以使用ID3模块，只不过设置参数：gain_ratio=True即可。

得到的决策树为：

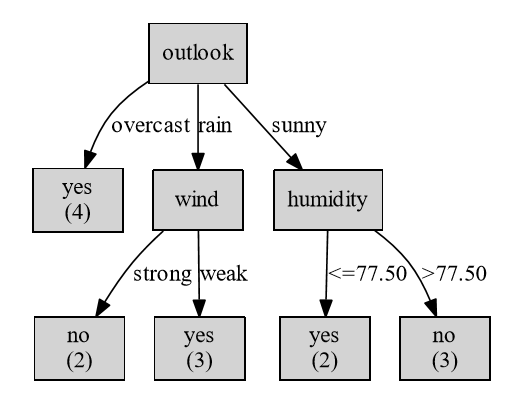
下面我们验证在sunny情况下，humidity的划分便准是否正确：

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
1	Sunny	Hot	85	Weak	No
2	Sunny	Hot	90	Strong	No
8	Sunny	Mild	95	Weak	No
9	Sunny	Cool	70	Weak	Yes
11	Sunny	Mild	70	Strong	Yes

首先计算humidity:

	70		85		90		95
	≤	>	≤	>	≤	>	≤	>
Yes	2	0	2	0	2	0	2	0
No	0	3	1	2	2	1	3	0
Entropy	0	0	0.756	0	0.846	0	0.971	0
Gain	0.971		0.517		0.294		0

Gain(humidity) = 0.971

Feature(humidity) = -2/5*log(-2/5) - 3/5*log(3/5) = 0.971（分两组，小于等于70的有2个数据，大于70的有3个数据）

RatioGain(humidity) = 1

Gain(Temperature) = 0.971 -  (-log(0.5) * 2/5) = 0.571

Feature(Temperature) = -2/5*log(-2/5)*2 - 1/5*log(1/5) = 1.522（分三组，分别有2、2、1个数据）

RatioGain(Temperature) = 0.375

Gain(Wind) = 0.971 - (3/5*(-1/3*log(1/3)-2/3*log(2/3)) + 2/5( -1/2*log(1/2)-1/2*log(1/2)))= 0.02

Feature(Wind) = 0.971

RatioGain(Wind) = 0.02

因此，程序得到的结果是对的。