项目一:项目第二天 Jquery ztree使用展示菜单数据 2、 基础设置需求分析 3、 搭建项目框架环境--ssh（复习） 4、 SpringData-JPA持久层入门案例（重点） 5、 Easyui menubutton菜单按钮使用 6、 Easyui messager消息框使用

1、 Jquery ztree使用展示菜单数据

2、 基础设置需求分析

3、 搭建项目框架环境--ssh（复习）

4、 SpringData-JPA持久层入门案例（重点）

5、 Easyui menubutton菜单按钮使用

6、 Easyui messager消息框使用

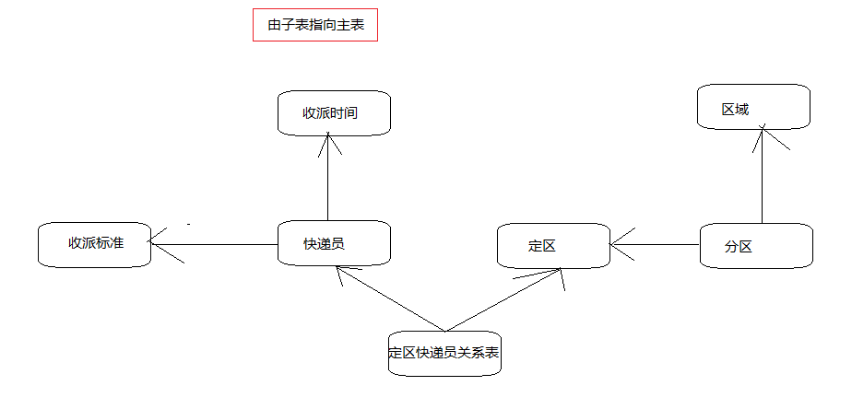
收派标准-快递员：一对多

收派时间-快递员：一对多

快递员-定区：多对多

一个快递员可以负责多个定区。一个定区可以被多个快递员负责。

 

区域-分区：一对多

一个区域可以包含多个分区。一个分区只能归属一个区域。

 

定区-分区：一对多

一个定区可以包含多个分区，一个分区只能属于一个定区。

1 使用ztree展示菜单数据（接上节课）

1、 Js代码中设置开启简单数据模式

var settings = {

data: {

simpleData: {

enable: true,   //启动简单数据模式：使用简单数据格式

idKey: "id",    //id:节点数据标识

pIdKey: "pId",  //pId：指定父节点

rootPId: 0      //根节点

}

}

}

2、 发送请求 请求json文件返回菜单数据，展示数据

 

----接下来如果点击菜单某个选项择弹出页面 所以需要去Ztree中找API

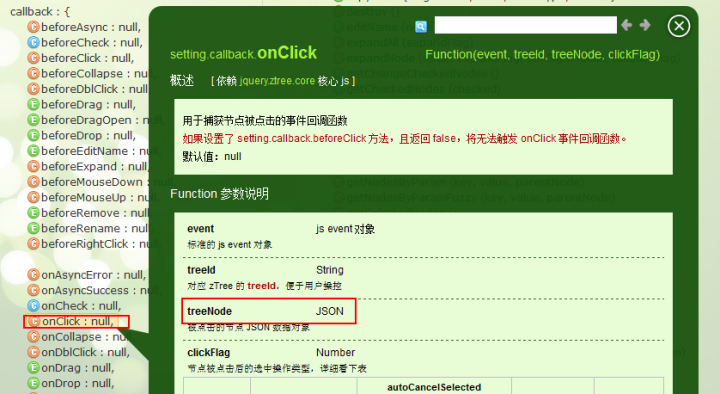
拼接跳转路径

callback: {

onClick: function(event, treeId, treeNode){

//treeNodeJSON 被点击的节点 JSON 数据对象

// alert(treeNode);

//将json对象输出在浏览器控制台

console.info(treeNode);

var r = $("#myTabs").tabs("exists",treeNode.name);

if(r){

//选中

$("#myTabs").tabs("select",treeNode.name);

}else{

//在中心区域 tabs选项卡面板中添加面板

$("#myTabs").tabs("add",{

title:treeNode.name,

closable:true,

这个属性需要记住  在点击左侧树形菜单之后 在中部的tabs选项卡中跳转 路径需要加入 Content属性 并引入 <iframe src=>

content:'<iframe src="../'+treeNode.page+'" width="100%" height="100%" frameborder="0"></iframe>'

});

}

}   //ztree节点数据单击事件

}

注:还需要判断 子节点是不可点的

Springdata-jpa实现原理：

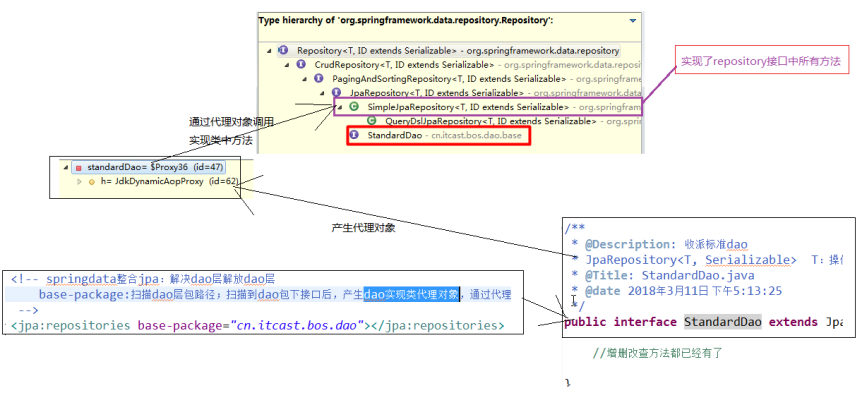
方式二：在自定义的方法上使用@Query注解，自己编写JPQL,或者sql语句。

1 easyui messager提示框 

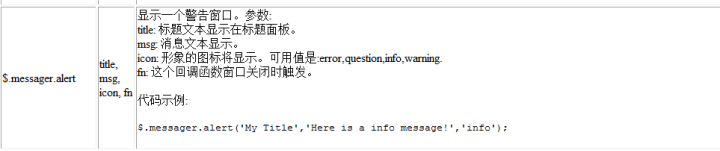
右下角的欢迎框