poj 2115 扩展欧几里得

题目链接：http://poj.org/problem?id=2115

题意：

给出一段循环程序，循环体变量初始值为 a，结束不等于 b ，步长为 c，看要循环多少次，其中运算限制在 k位；死循环输出FOREVER

那么这里就是：

(b-a)%gcd(c,n)==0，有解；否则无解。

有解的时候，有多少解呢？

求出来的解是：

这里就是： x * (b-a) / gcd(c,n)

其中最小的解又是多少呢？

定理：

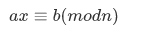
令 t = n / d;

最小的解是：(x%t+t)%t;

 #include <cstdio>
 #include <cmath>

 using namespace std;

 long long x,y;
 //d = gcd(a,b) = ax + by
 long long Extended_Euclid(long long a,long long b) {

     if(b==) {
         x = ;
         y = ;
         return a;
     }
     long long d = Extended_Euclid(b,a%b);
     long long tmp = x;
     x = y;
     y = tmp - a/b*y;
     return d;
 }

 int main()
 {
     long long a,b,c,k;
     while(scanf("%lld%lld%lld%lld",&a,&b,&c,&k)) {
         if(a==&&b==&&c==&&k==)
             break;
         long long n = (long long)<<k;
         long long d = Extended_Euclid(c,n);
         if((b-a)%d) {
             puts("FOREVER");
         }
         else {
             long long t = n/d;
             x = (x*(b-a)/d%t+t)%t;
             printf("%lld\n",x);
         }
     }

     return ;
 }