【The VC Dimension】林轩田机器学习基石

首先回顾上节课末尾引出来的VC Bound概念，对于机器学习来说，VC dimension理论到底有啥用。

三点：

1. 如果有Break Point证明是一个好的假设集合

2. 如果N足够大，那么Ein跟Eout的表现会比较接近

3. 如果算法A选的g足够好（Ein很小），则可能从数据中学到了东西

==================================================

现在正式引出VC Dimension的概念：啥叫VC Dimension:

VC Dimension是针对某个假设集合的一个性质。简言之，就是Break Point - 1的那个值的正式说法。如果没有Break Point，则VC Dimension是无限。

因此，VC Dimension有限被认为是好的。

为啥是好的呢？回顾之前几节的内容，有如下的结论证明VC Dimension有限是好的（样本充足情况下，可以保证Eout跟Ein接近）

马上举一个例子，证明VC Dimension的用处：

对于2D PLA来说：

1. 如果是linear separable D ， 则迭代次数足够，一定可以得到Ein(out)是0 （从训练集学到了东西）

2. 二维平面上 binary classification的VC Dimension是3，因此N足够大时候，Ein与Eout很接近（训练集的学习效果可以迁移到测试集）

端午放假出去散心。。。回来接着写。。。。

=======================================================================

在分析了1D perceptron和2D perceptron之后，猜测是否d-D perceptron的VC Dimension是d+1维呢？（这个猜测是可以证明成立的）

需要证明如下的式子：

先从第一个开始：

需要证明N=d+1时，某些情况下是可以shatter的即可。课件中举了这个例子：

举了这个例子，因为矩阵X是可逆的，不管Y的d+1维分量怎么取值（取0或1）组合，都可以求出来这样一个W。所以，证明了有些情况下d+1个inputs是可以被shatter的。

到这里，对可逆是咋回事已经要忘记了。

翻了翻课件（矩阵分析课程的）：

那么林的课件中的矩阵是依据啥构造出来的呢？我觉得是依据“A的行/列线性无关”这一条等价的性质构造出来的。

线性相关、无关是啥啊？

再翻一翻课件：

跟记忆中的差不多。

矩阵各种性质和运算操作太重要了，但是不想打断林这个课程的学习。搜到一个Brown大学的矩阵程序开发课程https://www.coursera.org/course/matrix，用python编写矩阵的各种操作，后续一定补上。

再证明后半部分：

1. 如果输入是d+2维的，那么一定可以构造出来第d+2个行向量是1~d+1个行向量的线性表示

2. 这时，如果WTX1~WTXd+1与其前面的系数a1~ad+1同号，则等式一定是大于零的；

3. 因此这个时候Yd+2就一定得是1，不可能取到0；也就是说，当Y1~Yd+1的取值跟a1~ad+1同号的情况下，Yd+2符号是定死的，所以Yd+2取不全01，因此无法shatter

下面看了DC Dimension的physical intuition

"effective binary" degree of freedom

可以粗略地理解为：free parameters

更深入了解一下VC Dimension的意义，主要从VC Bound入手。

可以集成到下面几张PPT中：

1. VC Bound是对模型复杂度的一个惩罚项

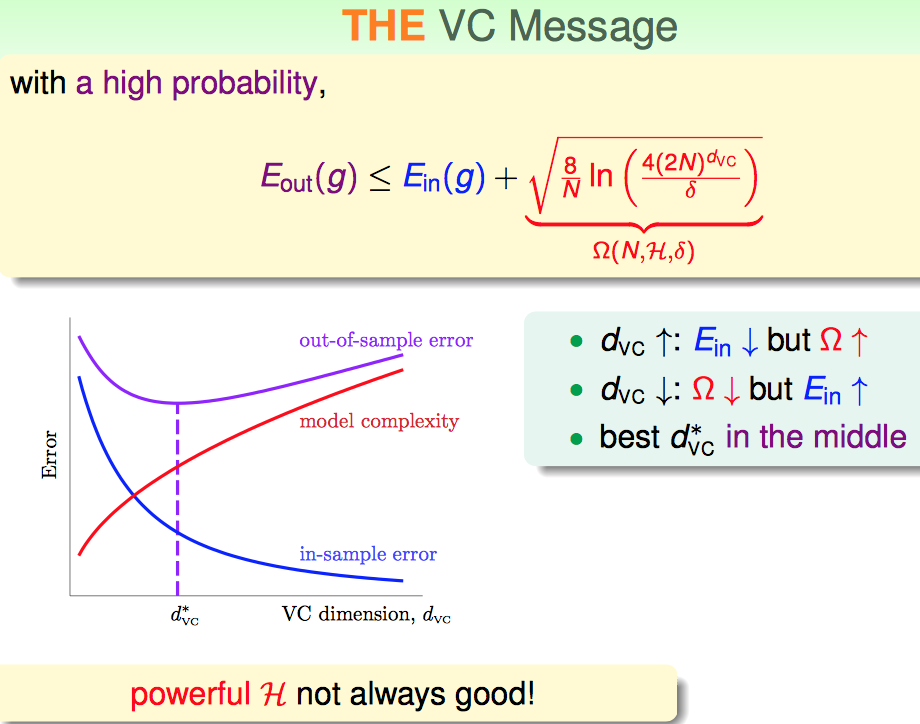
2. 可以根据VC Dimension来确定需要多大的样本量（实际经验一般是10倍的OK的）

3. VC Bound虽然是个非常宽松的Bound，但是却是一个通用性很强的Bound.