【bzoj2751】[HAOI2012]容易题(easy) 数论-快速幂

【bzoj2751】[HAOI2012]容易题(easy)

先考虑k=0的情况

那么第一个元素可能为[1,n] 如果序列长度为m-1时的答案是ans[m-1]

那么合并得

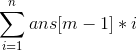
然后同理答案就是

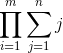
k很小 而且顺序可以随便交换

排序暴力减去就好了

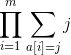
 /* http://www.cnblogs.com/karl07/ */
 #include <cstdlib>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 using namespace std;

 const int P=;
 int n,m,k,cnt=,sum,ans=;
 struct data{int x,y;}d[];
 int Q_pow(int x,int y){
     int ans=;
     while (y){
         if (y&) ans=1ll*ans*x%P;
         x=1ll*x*x%P;
         y=(y>>);
     }
     return ans;
 }
 bool oper(data a,data b) {return ((a.x<b.x) || (a.x==b.x && a.y<b.y));}

 int main(){
     scanf("%d%d%d",&n,&m,&k);
     sum=1ll*n*(n+)/%P;
     for (int i=;i<=k;i++){
         scanf("%d%d",&d[i].x,&d[i].y);
     }
     sort(d+,d+k+,oper);
     d[k+].x=-;
     d[k+].y=;
     for (int i=,s=1ll*(sum-d[].y+P)%P;i<=k+;i++){
         if (d[i].x!=d[i-].x) {ans=1ll*ans*s%P; s=sum; cnt++; }
         if (d[i].y!=d[i-].y || d[i].x!=d[i-].x) s=(s-d[i].y+P)%P;
     }
     printf("%lld\n",1ll*ans*Q_pow(sum,m-cnt)%P);
     return ;
 }

这么水的题想了半天。。没有调整负数WA了几发。。药丸。。