平衡树合集（Treap,Splay,替罪羊,FHQ Treap）

今天翻了翻其他大佬的博客，发现自己有些。。。颓废。。。

有必要洗心革面，好好学习

---

序：正常的BST有可能退化，成为链，大大降低效率，所以有很多方法来保持左右size的平衡，本文将简单介绍Treap，Splay，替罪羊，FHQ Treap；

另：代码都是普通平衡树

1.Treap

树堆，在数据结构中也称Treap，是指有一个随机附加域满足堆的性质的二叉搜索树，其结构相当于以随机数据插入的二叉搜索树。其基本操作的期望时间复杂度为O(logn)。相对于其他的平衡二叉搜索树，Treap的特点是实现简单，且能基本实现随机平衡的结构。——百度百科

好的treap=tree+heap（为何不叫hee??）

首先易知堆是棵二叉树，BST也是棵二叉树，

又易知：当堆的中的数据是随机插入（即不是有序数据&&有序插入），堆的的高度是趋于log级别的

于是我们让BST中的节点满足堆性质，让BST中的每一个节点带上一个随机权值dat，作为他在这个满足堆性质的BST中的优先级；

然后为了让BST中的节点满足堆性质，我们要rotate（旋）他

易知以下两种是等价的

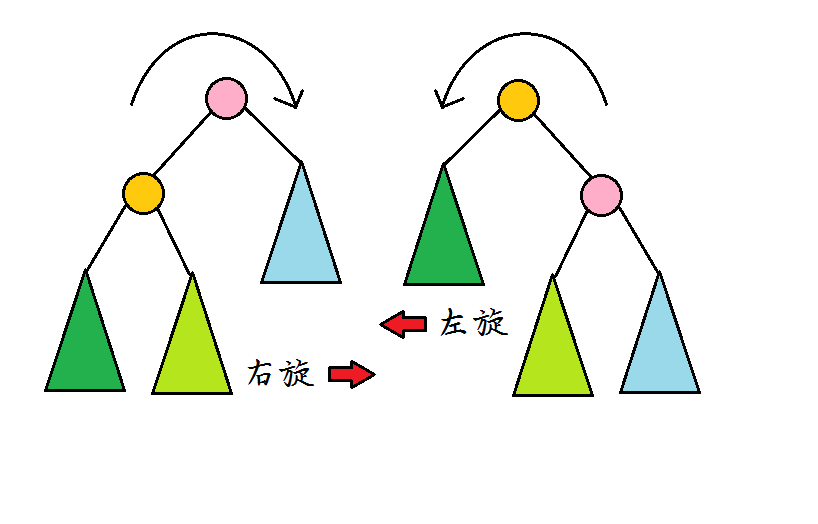
仍然满足BST的性质，但是改变了父子关系。

这就是如何在BST中维护堆性质：旋，改变父子关系，直到满足堆性质

PS：此处的旋好像叫单旋，只会改变父子关系，而Splay有一种操作较双旋（见下）

rotate（旋）在一类BST中我认为是最重要的操作

上代码：

ch[x][0/1]左右儿子，vl[x]权值，dat[x]在堆中的优先级，sz[x]子树大小，cnt[x]是vl[x]出现的次数

#include<cstdio>
#include<iostream>
#include<cstdlib>
#define ls ch[x][0]
#define rs ch[x][1]
#define R register int
using namespace std;
const int N=,Inf=0x3f3f3f3f;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
int n,tot,rt;
int sz[N],ch[N][],vl[N],dat[N],cnt[N];
inline void upd(int x) {sz[x]=sz[ls]+sz[rs]+cnt[x];}
inline int cre(int v) {R x=++tot; cnt[x]=,vl[x]=v,dat[x]=rand(),upd(x); return tot;}
inline void rot(int& x,int d) { R y=ch[x][d];
    ch[x][d]=ch[y][d^]; ch[y][d^]=x; upd(x),upd(y); x=y;
}
inline void ins(int& x,int v) {
    if(!x) {x=cre(v); return ;}
    if(vl[x]==v) {++cnt[x]; upd(x); return ;} R d=vl[x]<v;
    ins(ch[x][d],v); upd(x); if(dat[ch[x][d]]<dat[x]) rot(x,d);
}
inline void del(int& x,int v) {
    if(!x) return ; if(vl[x]==v) {
        if(cnt[x]>) --cnt[x]; else {
            if(!ls) x=rs; else if(!rs) x=ls;
            else {R d=dat[ls]>dat[rs]; rot(x,d); del(ch[x][d^],v);}//看谁大就把谁旋上来,把根旋下去
        }
    } else del(ch[x][vl[x]<v],v); upd(x);
}
inline void build() {srand(); rt=cre(-Inf); ins(rt,Inf);}
inline int getpre(int x,int v) {
    if(!x) return -Inf; if(vl[x]<v) return max(getpre(rs,v),vl[x]);//右边可能没有
    else return getpre(ls,v);
}
inline int getnxt(int x,int v) {
    if(!x) return Inf; if(vl[x]>v) return min(getnxt(ls,v),vl[x]);//同上
    else return getnxt(rs,v);
}
inline int getrk(int x,int v) {
    if(!x) return ;
    if(vl[x]==v) return sz[ls]+;
    else if(vl[x]>v) return getrk(ls,v);
    else return sz[ls]+cnt[x]+getrk(rs,v);
}
inline int getvl(int x,int rk) {
    if(!x||!rk) return ;
    if(rk<=sz[ls]) return getvl(ls,rk);
    else if(rk<=sz[ls]+cnt[x]) return x;
    return getvl(rs,rk-sz[ls]-cnt[x]);
}
signed main() { //freopen("in.in","r",stdin);freopen("out.out","w",stdout);
    n=g(); for(R i=;i<=n;++i) {
        R k=g(),x=g();
        if(k==) ins(rt,x); else if(k==) del(rt,x);
        else if(k==) printf("%d\n",getrk(rt,x));
        else if(k==) printf("%d\n",vl[getvl(rt,x)]);
        else if(k==) printf("%d\n",getpre(rt,x));
        else printf("%d\n",getnxt(rt,x));
    } //while(1);
} 

---

2.Splay

伸展树（Splay）是一种平衡二叉树，即优化后的二叉查找树。伸展树可以自我调整，这就要依靠伸展操作Splay(x,S)，使得提升效率。——洛谷日报

Splay，伸展树。。。维持左右子树平衡用到了另一种旋：双旋

设fa[x]=y,fa[y]=g

双旋，同时改变x,y与y,g之间的关系，它会使g变成x的孙子，y变为x的孩子，g变为y的孩子

分两种情况：

第一种如下

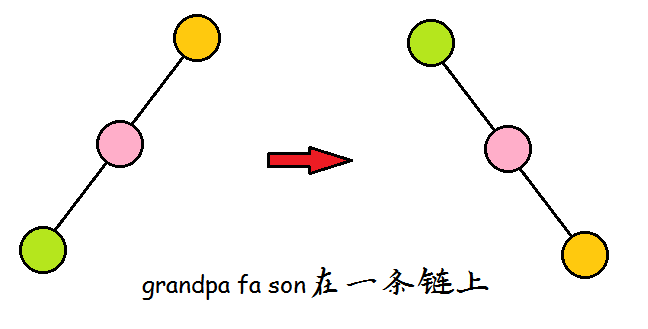
此时要先旋fa，再旋son（纯手绘不喜勿喷qwq）；

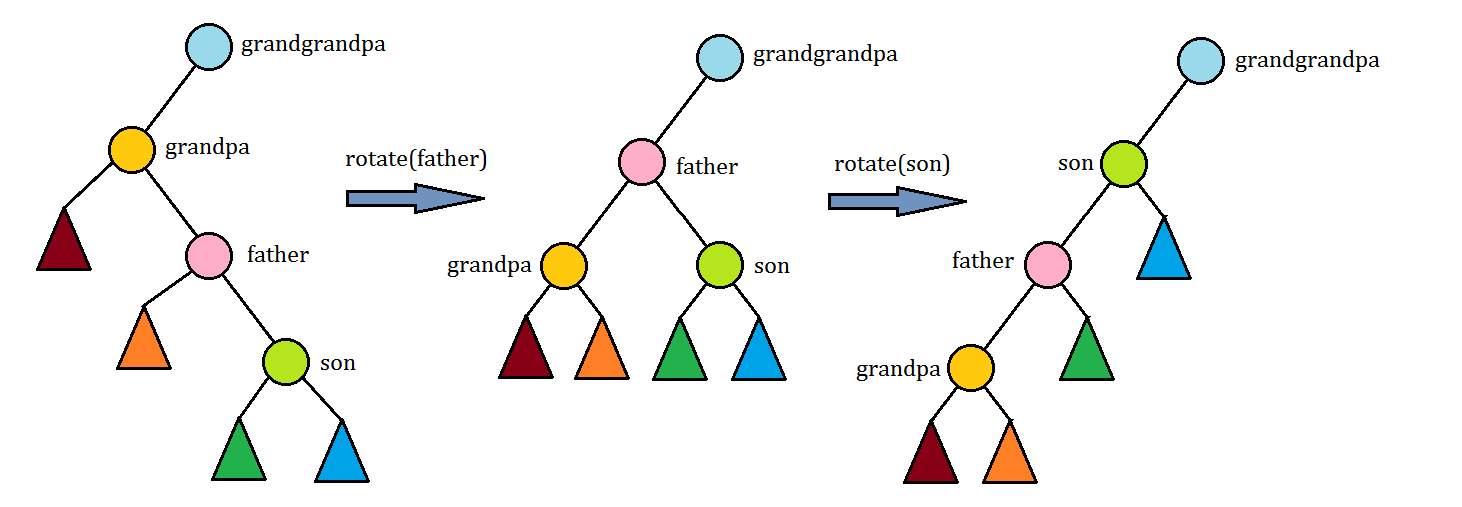
第二种如下（不在一条链）

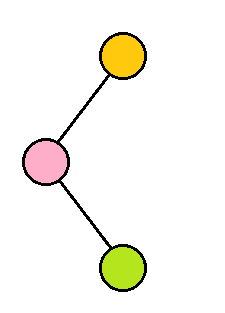
那么我们旋两次son

然后Splay的思路是：不管如何操作，将操作的点通过两种旋法，旋至根节点

至于为什么这么旋请找tarjan。。。至于时间复杂度请找tarjan

#include<cstdio>
#include<iostream>
#define R register int
#define ls (ch[x][0])
#define rs (ch[x][1])
const int N=,Inf=0x3f3f3f3f;
using namespace std;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
int n,tot;
int fa[N],ch[N][],sz[N],vl[N],cnt[N];
inline int cre(int v) {vl[++tot]=v,sz[tot]=cnt[tot]=; return tot;}
inline void upd(int x) {sz[x]=sz[ls]+cnt[x]+sz[rs];}
inline void rot(int x) {
    R y=fa[x],d=ch[y][]==x;
    if(fa[y]) ch[fa[y]][ch[fa[y]][]==y]=x;
    fa[x]=fa[y]; fa[ch[y][d]=ch[x][d^]]=y;
    fa[ch[x][d^]=y]=x; upd(y);
}
int rt;
inline void print(int x) {
    if(!x) return ; print(ls);
    printf("%d\n",vl[x]); print(rs);
}
inline void Splay(int x,int f) {
    while(fa[x]!=f) {
        R y=fa[x]; if(fa[y]!=f)
            rot((ch[y][]==x)==(ch[fa[y]][]==y)?y:x); //在不在一条链上
        rot(x);
    } upd(x); if(!f) rt=x;
}
inline void ins(int v) {
    R x=rt; while() {
        if(vl[x]==v) {++cnt[x]; break;}
        if(!ch[x][vl[x]<v]) {
            fa[ch[x][vl[x]<v]=cre(v)]=x;
            x=tot; break;
        } x=ch[x][vl[x]<v];
    } Splay(x,);
}
inline void build() {rt=cre(Inf),ins(-Inf);}
inline int getrk(int v) {
    R x=rt,ret=; while() {
        if(vl[x]==v) {ret+=sz[ls]+; Splay(x,); return ret;}
        if(vl[x]<v) ret+=sz[ls]+cnt[x];
        if(!ch[x][vl[x]<v]) {++ret; Splay(x,); return ret;}
        x=ch[x][vl[x]<v];
    }
}
inline int getpos(int x,int k) {
    if(!x) return ;
    if(k<=sz[ls]) return getpos(ls,k);
    if(k<=sz[ls]+cnt[x]) return x;
    return getpos(rs,k-sz[ls]-cnt[x]);
}
inline int getvl(int rk) {R x=getpos(rt,rk); Splay(x,); return vl[x];}
inline int getmx(int x,int y) {if(!x||!y) return x|y; return vl[x]>vl[y]?x:y;}
inline int ppos(int x,int v) {
    if(!x) return ; if(vl[x]<v) return getmx(x,ppos(rs,v));
    return ppos(ls,v);
}
inline int getpre(int v) {R x=ppos(rt,v); Splay(x,); return vl[x];}
inline int getmn(int x,int y) {if(!x||!y) return x|y; return vl[x]<vl[y]?x:y;}
inline int npos(int x,int v) {
    if(!x) return ; if(v<vl[x]) return getmn(x,npos(ls,v));
    return npos(rs,v);
}
inline int getnxt(int v) {R x=npos(rt,v); Splay(x,); return vl[x];}
inline void del(int v) {
    Splay(ppos(rt,v),),Splay(npos(rt,v),rt);
    R& x=ch[ch[rt][]][]; if(!(--cnt[x])) x=; else Splay(x,);
}
signed main() {
    //freopen("in.in","r",stdin);
    R n=g(); build(); while(n--) {
        R k=g(),x=g();
        if(k==) ins(x);
        else if(k==) del(x);
        else if(k==) printf("%d\n",getrk(x)-);
        else if(k==) printf("%d\n",getvl(x+));
        else if(k==) printf("%d\n",getpre(x));
        else printf("%d\n",getnxt(x));
    }
    //system("pause"); while(1);
}

---

3.替罪羊树

为何叫替罪羊。。。据说拍扁他是他儿子的锅。。。

替罪羊维护左右孩子平衡思路：当max(size(x.ls),size(x.rs))>size(x)*alpha（一个常量，一般0.7-0.8，看个人的喜好。。。），就暴力重构以x为根的子树。

具体地，就是把树拍扁，扔到数组中sort一遍，然后选mid,递归左子树和右子树；

然而替罪羊的删除是懒惰删除。。就是打一个tag。、所以用到儿子时要向下传递。。暴力重构时把删除的节点扔到内存池里去

所以， 特别地，当整个树实际存在的的节点数<整个树的节点数*B（另一个常量，合法范围是0.0-1.0，至于取多少看个人）

变量：sum总节点数=实际存在的节点数+删除的节点数； sz实际存在的节点数；del删除标记；mem存储删除的或没有使用的点；tmp存储拍扁重构的的点

#include<cstdio>
#include<iostream>
#define R register int
using namespace std;
const double A=0.72,RB=0.53;
const int N=;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
struct node{
    int ls,rs,vl,sz,sum,del;
    #define ls(x) t[x].ls
    #define rs(x) t[x].rs
    #define vl(x) t[x].vl
    #define sz(x) t[x].sz
    #define sum(x) t[x].sum
    #define del(x) t[x].del
}t[N];
int n,rt;
int mem[N],cm,tmp[N],ct;
inline bool ck(int x) {return (double)sz(x)*A<=(double)max(sz(ls(x)),sz(rs(x)));}
inline void dfs(int x) {
    if(!x) return ; dfs(ls(x));
    if(!del(x)) tmp[++ct]=x;
    else mem[++cm]=x;
    dfs(rs(x));
}
inline void build(int& x,int l,int r) {
    R md=l+r>>; x=tmp[md]; if(l==r) {
        ls(x)=rs(x)=del(x)=; sz(x)=sum(x)=; return ;
    } if(l<md) build(ls(x),l,md-); else ls(x)=;
    build(rs(x),md+,r);
    sz(x)=sz(ls(x))+sz(rs(x))+, sum(x)=sum(ls(x))+sum(rs(x))+;
}
inline void rebuild(int& x) {
    ct=; dfs(x); if(ct) build(x,,ct); else x=;
}
inline void ins(int& x,int vl) {
    if(!x) {
        x=mem[cm--]; vl(x)=vl,ls(x)=rs(x)=del(x)=; sz(x)=sum(x)=; return ;
    } ++sz(x),++sum(x);
    if(vl(x)>=vl) ins(ls(x),vl);
    else ins(rs(x),vl); if(ck(x)) rebuild(x);
}
inline int getrk(int vl) {
    R x=rt; R ret=; while(x) {
        if(vl(x)>=vl) x=ls(x);
        else {ret+=sz(ls(x))+(del(x)==); x=rs(x);}
    } return ret;
}
inline int getvl(int rk) {
    R x=rt; while(x) { //cout<<x<<" "<<vl(x)<<endl;
        if(del(x)==&&sz(ls(x))+==rk) return vl(x);
        else {
            if(sz(ls(x))+>rk) x=ls(x);
            else {
                rk-=sz(ls(x))+(del(x)==);
                x=rs(x);
            }
        }
    }
}
inline void delrk(int& x,int rk) {
    if(del(x)==&&sz(ls(x))+==rk) {del(x)=; --sz(x); return ;}
    --sz(x); if(sz(ls(x))+(del(x)==)>=rk) delrk(ls(x),rk);
    else delrk(rs(x),rk-sz(ls(x))-(del(x)==));
}
inline void delvl(int vl) { R x=getrk(vl); //cerr<<x<<endl;
    delrk(rt,x);
    if(sum(rt)*RB>=sz(rt)) rebuild(rt);
}
signed main() { //freopen("in.in","r",stdin); freopen("out.out","w",stdout);
    n=g(); for(R i=;i>=;--i) mem[++cm]=i;
    while(n--) {
        R k=g(),x=g();
        if(k==) ins(rt,x); else if(k==) delvl(x);
        else if(k==) printf("%d\n",getrk(x));
        else if(k==) printf("%d\n",getvl(x));
        else if(k==) printf("%d\n",getvl(getrk(x)-));
        else if(k==) printf("%d\n",getvl(getrk(x+)));
    } //while(1);
}

---

4.FHQ Treap

首先%%%fhq%%%

其次就是这个Treap不用旋，很好理解。。。

两个操作：split和merge

1.split(int o,int v,int& x,int& y) 把以o为根的树分<=v和>v的两部分

也可按照rank去分成两部分

2.merge(int x,int y) 合并以x和y为根的子树，返回新的根的值

短小而精悍。。。

#include<cstdio>
#include<iostream>
#include<cstdlib>
#define R register int
#define ls(i) ch[i][0]
#define rs(i) ch[i][1]
using namespace std;
const int N=;
inline int g() {
    R ret=,fix=; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-:fix;
    do ret=ret*+(ch^); while(isdigit(ch=getchar())); return ret*fix;
}
int tot;
int ch[N][],sz[N],vl[N],dat[N];
inline void upd(int x) {sz[x]=sz[ls(x)]+sz[rs(x)]+;}
inline int cre(int v) {R x=++tot; sz[x]=,vl[x]=v,dat[x]=rand();return x;}
inline int merge(int x,int y) {
    if(!x||!y) return x+y;
    if(dat[x]<dat[y]) {rs(x)=merge(rs(x),y); upd(x); return x;}
    else {ls(y)=merge(x,ls(y)); upd(y); return y;}
}
inline void split(int o,int v,int& x,int& y) {
    if(!o) {x=y=; return ;}
    if(vl[o]<=v) x=o,split(rs(o),v,rs(o),y);
    else y=o,split(ls(o),v,x,ls(o)); upd(o);
}
inline int getvl(int x,int rk) {
    while() { if(rk<=sz[ls(x)]) x=ls(x);
        else if(rk==sz[ls(x)]+) return x;
        else rk-=sz[ls(x)]+,x=rs(x);
    }
}
signed main() { srand(100023323u); R n,x,y,z,rt=; //freopen("1.in","r",stdin);freopen("out.out","w",stdout);
    n=g(); while(n--) {  //cerr<<n<<" "<<rt<<" "<<endl;
        R k=g(),a=g(); if(k==) split(rt,a,x,y),rt=merge(merge(x,cre(a)),y);
        else if(k==) {split(rt,a,x,z),split(x,a-,x,y); y=merge(ls(y),rs(y)),rt=merge(merge(x,y),z);}
        else if(k==) split(rt,a-,x,y),printf("%d\n",sz[x]+),rt=merge(x,y);
        else if(k==) printf("%d\n",vl[getvl(rt,a)]);
        else if(k==) split(rt,a-,x,y),printf("%d\n",vl[getvl(x,sz[x])]),rt=merge(x,y);
        else if(k==) split(rt,a,x,y),printf("%d\n",vl[getvl(y,)]),rt=merge(x,y);
    } while();
}

---

2019.05.05&&2019.05.06