tsne降维可视化

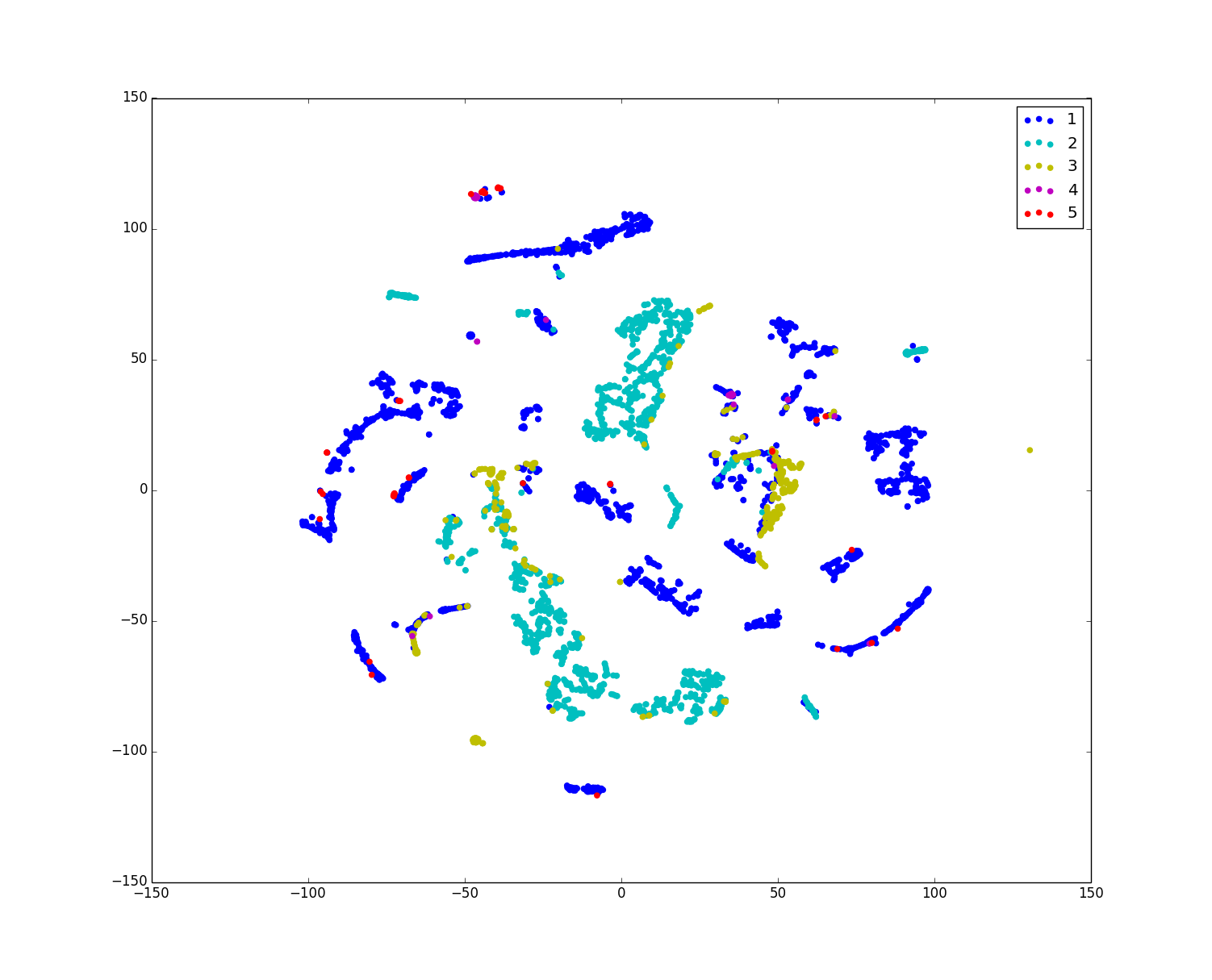
Python代码：准备训练样本的数据和标签：train_X4000.txt、train_y4000.txt 放于tsne.py当前目录.（具体t-SNE – Laurens van der Maaten http://lvdmaaten.github.io/tsne/，Python implementation）,

tsne.py代码：（为了使得figure显示数据的标签，代码做了简单修改）

#!/usr/bin/env python
# -*- coding: utf-8 -*-

#
#  tsne.py
#
# Implementation of t-SNE in Python. The implementation was tested on Python 2.5.1, and it requires a working
# installation of NumPy. The implementation comes with an example on the MNIST dataset. In order to plot the
# results of this example, a working installation of matplotlib is required.
# The example can be run by executing: ipython tsne.py -pylab
#
#
#  Created by Laurens van der Maaten on 20-12-08.
#  Copyright (c) 2008 Tilburg University. All rights reserved.

import numpy as Math
import pylab as Plot

def Hbeta(D = Math.array([]), beta = 1.0):
    """Compute the perplexity and the P-row for a specific value of the precision of a Gaussian distribution."""

    # Compute P-row and corresponding perplexity
    P = Math.exp(-D.copy() * beta);
    sumP = sum(P)+1e-6;
    H = Math.log(sumP) + beta * Math.sum(D * P) / sumP;
    P = P / sumP;
    return H, P;

def x2p(X = Math.array([]), tol = 1e-5, perplexity = 30.0):
    """Performs a binary search to get P-values in such a way that each conditional Gaussian has the same perplexity."""

    # Initialize some variables
    print "Computing pairwise distances..."
    (n, d) = X.shape;
    sum_X = Math.sum(Math.square(X), 1);
    D = Math.add(Math.add(-2 * Math.dot(X, X.T), sum_X).T, sum_X);
    P = Math.zeros((n, n));
    beta = Math.ones((n, 1));
    logU = Math.log(perplexity);

    # Loop over all datapoints
    for i in range(n):

        # Print progress
        if i % 500 == 0:
            print "Computing P-values for point ", i, " of ", n, "..."

        # Compute the Gaussian kernel and entropy for the current precision
        betamin = -Math.inf;
        betamax =  Math.inf;
        Di = D[i, Math.concatenate((Math.r_[0:i], Math.r_[i+1:n]))];
        (H, thisP) = Hbeta(Di, beta[i]);

        # Evaluate whether the perplexity is within tolerance
        Hdiff = H - logU;
        tries = 0;
        while Math.abs(Hdiff) > tol and tries < 50:

            # If not, increase or decrease precision
            if Hdiff > 0:
                betamin = beta[i].copy();
                if betamax == Math.inf or betamax == -Math.inf:
                    beta[i] = beta[i] * 2;
                else:
                    beta[i] = (beta[i] + betamax) / 2;
            else:
                betamax = beta[i].copy();
                if betamin == Math.inf or betamin == -Math.inf:
                    beta[i] = beta[i] / 2;
                else:
                    beta[i] = (beta[i] + betamin) / 2;

            # Recompute the values
            (H, thisP) = Hbeta(Di, beta[i]);
            Hdiff = H - logU;
            tries = tries + 1;

        # Set the final row of P
        P[i, Math.concatenate((Math.r_[0:i], Math.r_[i+1:n]))] = thisP;

    # Return final P-matrix
        print "Mean value of sigma: ", Math.mean(Math.sqrt(1 / beta))
    return P;

def pca(X = Math.array([]), no_dims = 50):
    """Runs PCA on the NxD array X in order to reduce its dimensionality to no_dims dimensions."""

    print "Preprocessing the data using PCA..."
    (n, d) = X.shape;
    X = X - Math.tile(Math.mean(X, 0), (n, 1));
    (l, M) = Math.linalg.eig(Math.dot(X.T, X));
    Y = Math.dot(X, M[:,0:no_dims]);
    return Y;

def tsne(X = Math.array([]), no_dims = 2, initial_dims = 50, perplexity = 30.0):
    """Runs t-SNE on the dataset in the NxD array X to reduce its dimensionality to no_dims dimensions.
    The syntaxis of the function is Y = tsne.tsne(X, no_dims, perplexity), where X is an NxD NumPy array."""

    # Check inputs
    if X.dtype != "float64":
        print "Error: array X should have type float64.";
        return -1;
    #if no_dims.__class__ != "":            # doesn't work yet!
    #    print "Error: number of dimensions should be an integer.";
    #    return -1;

    # Initialize variables
    X = pca(X, initial_dims).real;
    (n, d) = X.shape;
    max_iter = 1000
    initial_momentum = 0.5;
    final_momentum = 0.8;
    eta = 500;
    min_gain = 0.01;
    Y = Math.random.randn(n, no_dims);
    dY = Math.zeros((n, no_dims));
    iY = Math.zeros((n, no_dims));
    gains = Math.ones((n, no_dims));

    # Compute P-values
    P = x2p(X, 1e-5, perplexity);
    P = P + Math.transpose(P);
    P = P / (Math.sum(P));
    P = P * 4;                                    # early exaggeration
    P = Math.maximum(P, 1e-12);

    # Run iterations
    for iter in range(max_iter):

        # Compute pairwise affinities
        sum_Y = Math.sum(Math.square(Y), 1);
        num = 1 / (1 + Math.add(Math.add(-2 * Math.dot(Y, Y.T), sum_Y).T, sum_Y));
        num[range(n), range(n)] = 0;
        Q = num / Math.sum(num);
        Q = Math.maximum(Q, 1e-12);

        # Compute gradient
        PQ = P - Q;
        for i in range(n):
            dY[i,:] = Math.sum(Math.tile(PQ[:,i] * num[:,i], (no_dims, 1)).T * (Y[i,:] - Y), 0);

        # Perform the update
        if iter < 20:
            momentum = initial_momentum
        else:
            momentum = final_momentum
        gains = (gains + 0.2) * ((dY > 0) != (iY > 0)) + (gains * 0.8) * ((dY > 0) == (iY > 0));
        gains[gains < min_gain] = min_gain;
        iY = momentum * iY - eta * (gains * dY);
        Y = Y + iY;
        Y = Y - Math.tile(Math.mean(Y, 0), (n, 1));

        # Compute current value of cost function
        if (iter + 1) % 10 == 0:
            C = Math.sum(P * Math.log(P / Q));
            print "Iteration ", (iter + 1), ": error is ", C

        # Stop lying about P-values
        if iter == 100:
            P = P / 4;

    # Return solution
    return Y;

if __name__ == "__main__":
    print "Run Y = tsne.tsne(X, no_dims, perplexity) to perform t-SNE on your dataset."
    print "Running example on 2,500 MNIST digits..."
    X = Math.loadtxt("train_X4000.txt");
#X = X[:100]
    labels = Math.loadtxt("train_y4000.txt");
#labels = labels[:100]
    Y = tsne(X, 2, 38, 20.0);
    fil = open('Y.txt','w')
    for i in Y:
        fil.write(str(i[0])+' '+str(i[1])+'\n')
    fil.close()
    colors=['b', 'c', 'y', 'm', 'r']
    idx_1 = [i1 for i1 in range(len(labels)) if labels[i1]==1]
    flg1=Plot.scatter(Y[idx_1,0], Y[idx_1,1], 20,color=colors[0],label='1');
    idx_2= [i2 for i2 in range(len(labels)) if labels[i2]==2]
    flg2=Plot.scatter(Y[idx_2,0], Y[idx_2,1], 20,color=colors[1], label='2');
    idx_3= [i3 for i3 in range(len(labels)) if labels[i3]==3]
    flg3=Plot.scatter(Y[idx_3,0], Y[idx_3,1], 20, color=colors[2],label='3');
    idx_4= [i4 for i4 in range(len(labels)) if labels[i4]==4]
    flg4=Plot.scatter(Y[idx_4,0], Y[idx_4,1], 20,color=colors[3], label='4');
    idx_5= [i5 for i5 in range(len(labels)) if labels[i5]==5]
    flg5=Plot.scatter(Y[idx_5,0], Y[idx_5,1], 20, color=colors[4],label='5');
#    flg=Plot.scatter(Y[:,0], Y[:,1], 20,labels);
    Plot.legend()
    Plot.savefig('figure4000.pdf')
    Plot.show()