hdu---(1054)Strategic Game(最小覆盖边)

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5034    Accepted Submission(s): 2297

Problem Description

Bob
enjoys playing computer games, especially strategic games, but
sometimes he cannot find the solution fast enough and then he is very
sad. Now he has the following problem. He must defend a medieval city,
the roads of which form a tree. He has to put the minimum number of
soldiers on the nodes so that they can observe all the edges. Can you
help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The
node identifiers are integer numbers between 0 and n-1, for n nodes (0
< n <= 1500). Every edge appears only once in the input data.

For example for the tree:

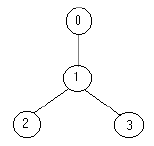
the solution is one soldier ( at the node 1).

The
output should be printed on the standard output. For each given input
data set, print one integer number in a single line that gives the
result (the minimum number of soldiers). An example is given in the
following table:

 

Sample Input

4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)

 

Sample Output

1
2

 

Source

Southeastern Europe 2000

 

Recommend

 

代码：  这里是最少覆盖边，开始一直搞最小覆盖点，然后各种不得劲，.....后面看了以下提示，然后就明白了。但是改了之后有开始tie,没办法，只能最后用起了邻接表（我用 的是vector来替代的）  最小覆盖点 =顶点数- 最大匹配数  、  最小覆盖边= 等于（无向图）最大匹配/2;

 

代码：

 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<iostream>
 using namespace std;
 const int maxn=;
 vector<vector<int> >grid(maxn);
 bool vis[maxn];
 int savx[maxn];
 int n;
 int km(int x){
     vector<int>::iterator it;
   for(it=grid[x].begin();it<grid[x].end();it++){
       if(!vis[*it]){
            vis[*it]=;
       if(savx[*it]==-||km(savx[*it])){
         savx[*it]=x;
         return ;
       }
       }
   }
  return ;
 }

 int main(){
     int ans=;
     int a,b,c;
     int km(int );
     while(scanf("%d",&n)!=EOF){
         ans=;
        memset(savx,-,sizeof(savx));
        for(int i=;i<n;i++)
           grid[i].clear();
       for(int i=;i<n;i++){
            scanf("%d:(%d)",&a,&b);
           for(int j=;j<b;j++){
          scanf("%d",&c);
          grid[a].push_back(c);
          grid[c].push_back(a);
           }
       }
      for(int i=;i<n;i++){
        memset(vis,,sizeof(vis));
        ans+=km(i);
      }
     printf("%d\n",ans/);
     }
  return ;
 }