【阅读笔记】低照度图像增强-《Fast efficient algorithm for enhancement of low lighting video》

本文介绍的是一种比较实用的低照度图像增强效果很好的方法，Xuan Dong论文《Fast efficient algorithm for enhancement of low lighting video》

概述

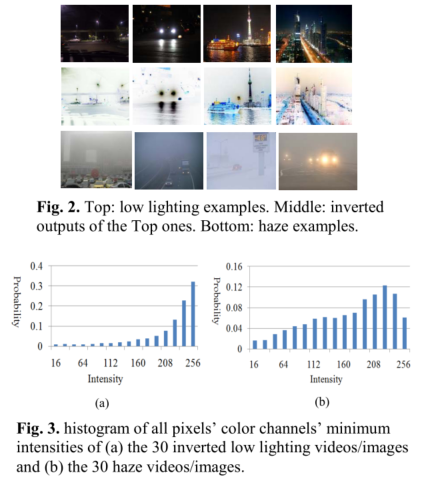
低光照图像取反（255 - 低光照图像），和有雾图像存在一些共性，比如在天空或者遥远的背景这些地方，亮度值都是很高的，但在近景的 RGB 三通道中至少有一个亮度值很低。作者提出直接用去雾算法对低光照图像的反转图像处理，去雾结果再取反得到低照度增强结果。

低照度图像增强算法

大气散射模型

大多透雾算法基于大气散射模型，模型如下：

I

(

x

)

=

J

(

x

)

t

(

x

)

+

A

(

1

−

t

(

x

)

)

I (x) = J (x)t(x) + A(1 − t(x))

I(x)=J(x)t(x)+A(1−t(x))

其中，

I

(

x

)

I(x)

I(x)表示含雾图，

J

(

x

)

J(x)

J(x)表示无雾图，

A

A

A表示大气光模型，

t

(

x

)

=

e

−

β

d

(

x

)

t(x)=e^{- \beta d(x)}

t(x)=e−βd(x)表示传输率矩阵，

β

\beta

β 表示大气散射系数，

d

(

x

)

d(x)

d(x)表示图像区域的景深。雾越浓，到达相机的物体反射的光越少，即传输率越小。

​上式可以改写为：

J

(

x

)

=

I

(

x

)

−

A

t

(

x

)

+

A

J (x) = \frac{I (x) - A}{t(x)}+A

J(x)=t(x)I(x)−A​+A

为了得到

J

(

x

)

J(x)

J(x)，重点在估计

A

A

A和

t

(

x

)

t(x)

t(x)。

暗通道先验知识：

在大部分无雾图像的无天空区域，像素中至少存在一个颜色通道存在很低非常低的亮度值。这个最低的亮度值几乎等同于0。因此，对于一个观测图像J，其暗通道趋近于0，即

J

d

a

r

k

(

X

)

=

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

∈

r

,

g

,

b

J

c

(

y

)

)

→

0

J^{dark}(X) = min_{y \in \Omega (x)}(min_{c \in {r,g,b }} J^{c}(y)) \to 0

Jdark(X)=miny∈Ω(x)​(minc∈r,g,b​Jc(y))→0

其中，

J

c

J^{c}

Jc表示彩色图像每个通道，

Ω

(

x

)

\Omega(x)

Ω(x)表示以

x

x

x为中心的窗口

透雾算法

基于大气散射模型，透雾模型的方法步骤如下：

1、从雾图I (x) 估计传输率矩阵t(x)

2、估计大气光值A

3、通过公式估计无雾图J(x)

首先求出每个像素RGB分量中的最小值，存入一副和原始图像大小相同的灰度图中，然后再对这幅灰度图进行最小值滤波，滤波的半径由窗口大小决定，一般有

W

i

n

d

o

w

S

i

z

e

=

2

∗

R

a

d

i

u

s

+

1

WindowSize = 2 * Radius + 1

WindowSize=2∗Radius+1

将雾模型

I

(

x

)

=

J

(

x

)

t

(

x

)

+

A

(

1

−

t

(

x

)

)

I (x) = J (x)t(x) + A(1 − t(x))

I(x)=J(x)t(x)+A(1−t(x))

处理为：

I

c

(

x

)

A

c

=

J

c

(

x

)

A

c

t

(

x

)

+

1

−

t

(

x

)

\frac{I^{c} (x)}{A^{c}} = \frac{J^{c} (x)}{A^{c}}t(x) + 1 − t(x)

AcIc(x)​=AcJc(x)​t(x)+1−t(x)

假设在窗口内透射率$ t(x)

为常数，定义为

为常数，定义为

为常数，定义为\tilde t(x)

，

，

，A$值已知。对上式求两次最小值运算，得到

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

I

c

(

y

)

A

c

)

=

t

~

(

x

)

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

J

c

(

y

)

A

c

)

+

1

−

t

~

(

x

)

\underset {y \in \Omega (x)}{min}(\underset{c}{min} \frac{I^{c} (y)}{A^{c}}) = \tilde t(x) \underset {y \in \Omega (x)}{min}(\underset{c}{min} \frac{J^{c} (y)}{A^{c}})+ 1 − \tilde t(x)

y∈Ω(x)min​(cmin​AcIc(y)​)=t~(x)y∈Ω(x)min​(cmin​AcJc(y)​)+1−t~(x)

根据暗原色先验理论

J

d

a

r

k

(

x

)

=

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

J

c

(

y

)

)

=

0

J^{dark}(x) = \underset {y \in \Omega (x)}{min}(\underset{c }{min} J^{c}(y)) = 0

Jdark(x)=y∈Ω(x)min​(cmin​Jc(y))=0

推导出

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

J

c

(

y

)

A

c

)

=

0

\underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{J^{c}(y)}{A^{c}}) = 0

y∈Ω(x)min​(cmin​AcJc(y)​)=0

带入透射率为常数的公式，得到透射率预估值

t

~

(

x

)

=

1

−

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

I

c

(

y

)

A

c

)

\tilde t(x) = 1-\underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{I^{c}(y)}{A^{c}})

t~(x)=1−y∈Ω(x)min​(cmin​AcIc(y)​)

上式添加一个限制系数，得到

t

~

(

x

)

\tilde t(x)

t~(x)：

t

~

(

x

)

=

1

−

ω

m

i

n

y

∈

Ω

(

x

)

(

m

i

n

c

I

c

(

y

)

A

c

)

\tilde t(x) = 1-\omega\underset {y \in \Omega (x)}{min}(\underset{c }{min} \frac{I^{c}(y)}{A^{c}})

t~(x)=1−ωy∈Ω(x)min​(cmin​AcIc(y)​)

ω

\omega

ω取值0.95

以上假设全球达气光A值时已知的，在实际中，我们可以借助于暗通道图来从有雾图像中获取该值。具体步骤如下：

1）从暗通道图中按照亮度的大小取前0.1%的像素。

​2）在这些位置中，在原始有雾图像I中寻找对应的具有最高亮度的点的值，作为

A

A

A值。

算法参数优化

文中自适应调节

t

(

x

)

t(x)

t(x)，如下式

t

′

(

x

)

=

{

2

∗

t

(

x

)

,

0

<

t

(

x

)

<

0.5

1

,

0.5

<

t

(

x

)

<

1

t'(x) = \begin{cases} 2*t(x),0<t(x)<0.5\\1,0.5<t(x)<1 \end{cases}

t′(x)={2∗t(x),0<t(x)<0.51,0.5<t(x)<1​

优化

t

(

x

)

t(x)

t(x)如下,增强暗区提亮，亮区微处理，效果更好

t

′

(

x

)

=

{

t

(

x

)

2

∗

2

,

0

<

t

(

x

)

<

0.5

t

(

x

)

,

0.5

<

t

(

x

)

<

1

t'(x) = \begin{cases} t(x)^2*2,0<t(x)<0.5\\t(x),0.5<t(x)<1 \end{cases}

t′(x)={t(x)2∗2,0<t(x)<0.5t(x),0.5<t(x)<1​

效果对比

图、测试图像1、原文处理效果、算法优化处理效果

图、测试图像2、原文处理效果、算法优化处理效果

图、测试图像3、原文处理效果、算法优化处理效果 ## 算法总结 简单易实现的增强算法，普世性较好，透雾算法处理部分兼容各种透雾算法。

算法实现参考

https://github.com/AomanHao/ISP_Low_Light_Image_Enhancement

我的个人博客主页，欢迎访问

我的CSDN主页，欢迎访问

我的GitHub主页，欢迎访问

我的个人博客主页，欢迎访问

我的CSDN主页，欢迎访问

我的GitHub主页，欢迎访问