线性dp：最长公共子串

最长公共子串

• 本文讲解的题与leetcode718.最长重复子数组，题意一模一样，阅读完本文以后可以去挑战这题。

力扣链接

题目叙述：

给定两个字符串，输出其最长公共子串的长度。

输入

ABACCB
AACCAB

输出

3

解释

最长公共子串是ACC，其长度为3。

与最长公共子序列的区别

• 公共子串：字符必须是连续相等的
• 公共子序列：字符必须是相等的，可以不连续。

动态规划思路

• 只有当两个字符串中的字符连续相等的时候，公共子串的长度才不断增加，否则清零
• 因此，我们不难发现，公共子串问题其实是公共子序列问题的一个特殊情况

状态变量以及其含义

• 我们延续最长公共子序列的思路，可以使用两个指针变量，i和j来遍历a，b字符串。
• 那么我们的f[i][j]代表着什么呢？因为本题是要连续的子串，因此我们的 f[i][j]表示以a[i]和b[j]为结尾的公共子串的长度

递推公式

• 那么，我们很容易的就可以得出递推公式：
  • f[i][j]=f[i-1][j-1]+1（a[i]==b[j]）
  • f[i][j]=0）（a[i]!=b[j]）
• 边界条件为：
  • f[0][j]=0
  • f[i][0]=0

遍历顺序：

• 显然是从上到下，从左到右。

如何初始化？

• 处理好上面所说的边界条件，并且根据递推公式来进行初始化f数组即可。

举例打印dp数组

• 举例如如图所示：

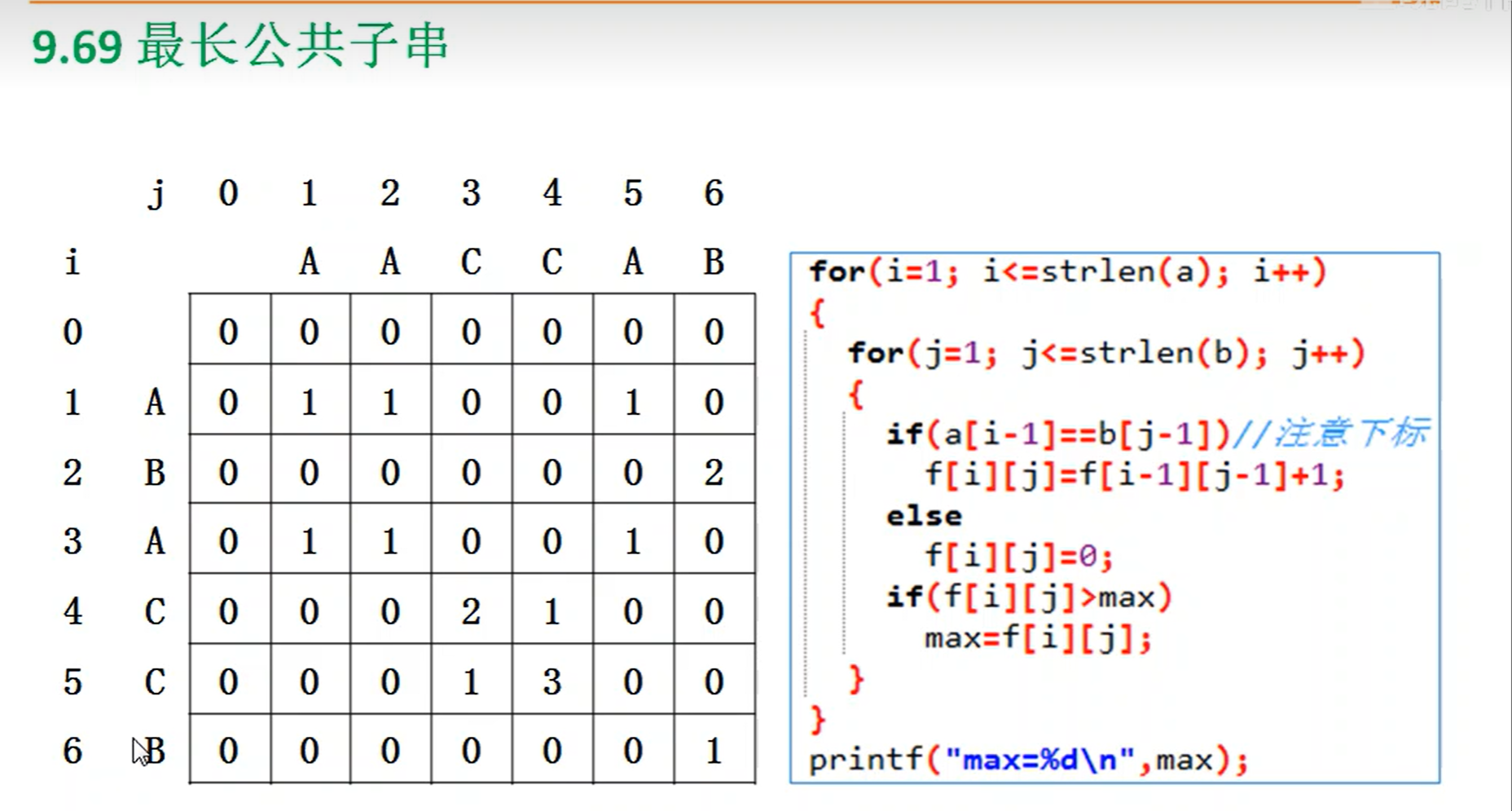
• f[i][j] 的值如图所示。

最终代码实现

#include<iostream>
#include<cstring>
using namespace std;

char a[200]="BCCABCCB";
char b[200]="AACCAB";
int f[201][201];

int main(){
  int ans=0;
  for(int i=1; i<=strlen(a); i++){
    for(int j=1; j<=strlen(b); j++){
      if(a[i-1]==b[j-1]) f[i][j]=f[i-1][j-1]+1;
      ans=max(ans,f[i][j]);
    }
  }
  printf("ans=%d\n",ans);
  return 0;
}