VINS中的重力-尺度-速度初始化（2）

细化重力

\(\quad\)上一篇文章中得到的 \(g\) 一般是存在误差的。因为在实际应用中，当地的重力向量的模一般是已知固定大小的（所以只有两个自由度未知），而我们在前面求解时并没有利用这个条件，因此最后计算出来的重力向量很难刚好满足这个条件。于是，在vins的初始化中，还会对得到的重力向量进行修正。

\(\quad\)首先，作者对重力向量进行参数化：

\[\hat{g}=\|g\| \overline{\hat{g}}+w_{1} b_{1}+w_{2} b_{2}=\|g\| \overline{\hat{g}}+\vec{b}^{3 \times 2} w^{2 \times 1}
\]

其中，\(\overline{\hat{g}}\)是上一步中估计得到的重力向量方向的单位向量，\(b_1\)与\(b_2\)是另外两个单位向量，是\(\overline{\hat{g}}\)切平面上的两个互相垂直的单位向量，获得方式如下：

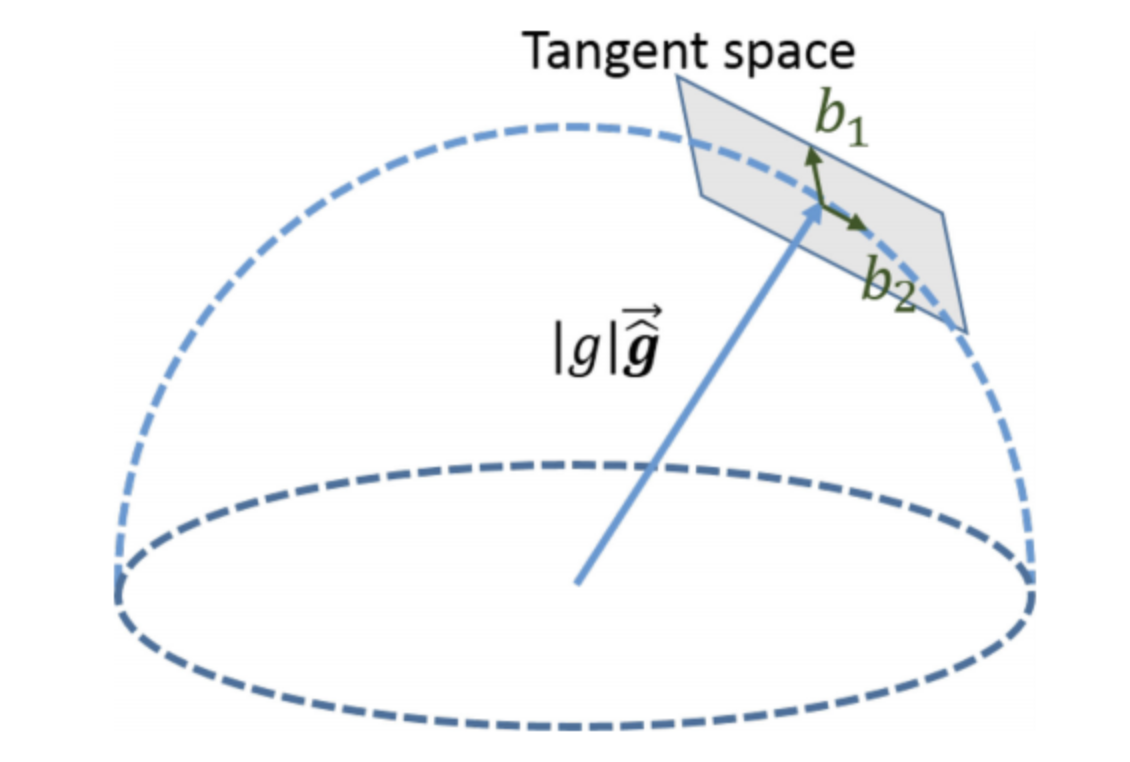
此时我们可以从上面的式子知道，原本三维的优化变量 \(g^{c 0}\) 已经可以使用两维的 \(w^{2 \times 1}\) 替代。参考上一节的推导，待优化变量变成了

\[\left[\begin{array}{c}
v_{b_{k}}^{b_{k}} \\
v_{b_{k+1}}^{b_{k+1}} \\
w^{2 \times 1} \\
s
\end{array}\right]
\]

最后得到的观测方程也变为了

\[\left[\begin{array}{cccc}
-I \Delta t_{k} & 0 & \frac{1}{2} R_{c_{0}}^{b_{k}} \Delta t_{k}^{2} \vec{b} & R_{c_{0}}^{b_{k}}\left(p_{c_{k+1}}^{c_{0}}-p_{c_{k}}^{c_{0}}\right) \\
-I & R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} & R_{c_{0}}^{b_{k}} \Delta t_{k} \vec{b} & 0
\end{array}\right]\left[\begin{array}{c}
v_{b_{k}}^{b_{k}} \\
v_{b_{k+1}}^{b_{k+1}} \\
w \\
s
\end{array}\right]=\left[\begin{array}{c}
\alpha_{b_{k+1}}^{b_{k}}+R_{c_{0}}^{b_{k}} R_{b_{k+1}}^{c_{0}} p_{c}^{b}-p_{c}^{b}-\frac{1}{2} R_{c_{0}}^{b_{c}} \Delta t_{k}^{2}\|g\| \hat{\hat{g}} \\
\beta_{b_{k+1}}^{b_{k}}-R_{c_{0}}^{b_{k}} \Delta t_{k}\|g\| \hat{g}
\end{array}\right]
\]

基于新得到的观测方程（可以使用LDLT分解求解），我们可以通过重力约束不断地对初始化结果进行修正，迭代对其进行求解（vins中迭代了4次），最后得到一个修正后的初始化结果。

与世界坐标系对齐

这一步一般是最后一步，一般世界坐标系选择的是东北天坐标系。则这个对齐操作就是得到将重力向量旋转到Z轴上的旋转矩阵，这个旋转矩阵就是将原本坐标变换到世界坐标系（东北天坐标系）的变换矩阵。

找到这个变换矩阵后，接下来就是使用这个变换矩阵将位姿，速度等状态信息都变换到世界坐标系下。

加速度计bias

通过上面的阅读，我们会发现在vins的初始化中并没有对加速度计的bias进行估计，感觉对于超定的方程，多计算一个加速度计的bias好像也不是什么难事，，而且建模应该会更准确。在这个初始化工作的论文中其实有解释原因：

通过仿真实验证明，如果运动不剧烈，加速度计的bias很难被观测出来；
忽略加速计的bias对估计其他初始值的影响不大；
加速度计的bias是可以通过之后的VIO紧耦合优化，慢慢估计出来的；

参考资料

[1] https://github.com/HKUST-Aerial-Robotics/VINS-Mono
[2] VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator, Tong Qin, Peiliang Li, Zhenfei Yang, Shaojie Shen, IEEE Transactions on Robotics
[3] https://xhy3054.github.io/