机器学习笔记8:XGBoost
目录
参考地址:
贪心学院:https://github.com/GreedyAIAcademy/Machine-Learning
1 回顾一下决策树
学习XGBoost过程中险些把之前决策数的知识也弄迷茫了,因此首先回顾一下决策树
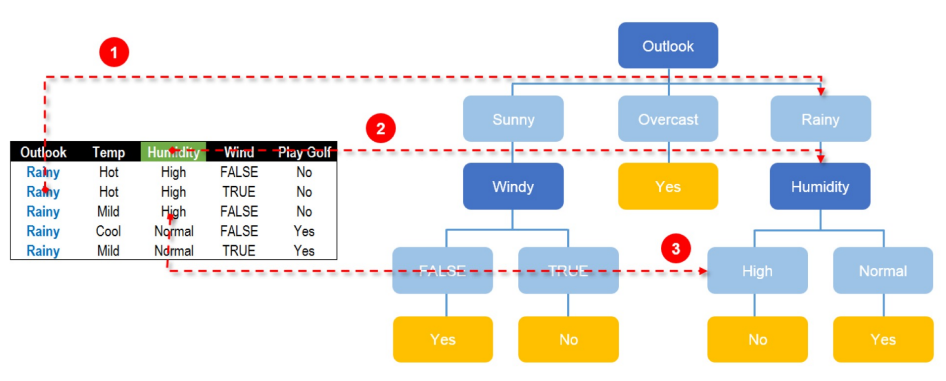
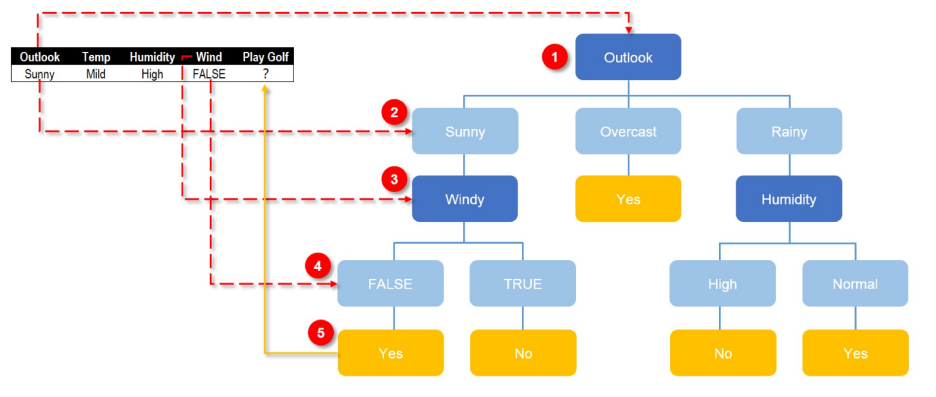
据信息熵来的,也就是信息熵大的字段会更靠近决策树的根节点
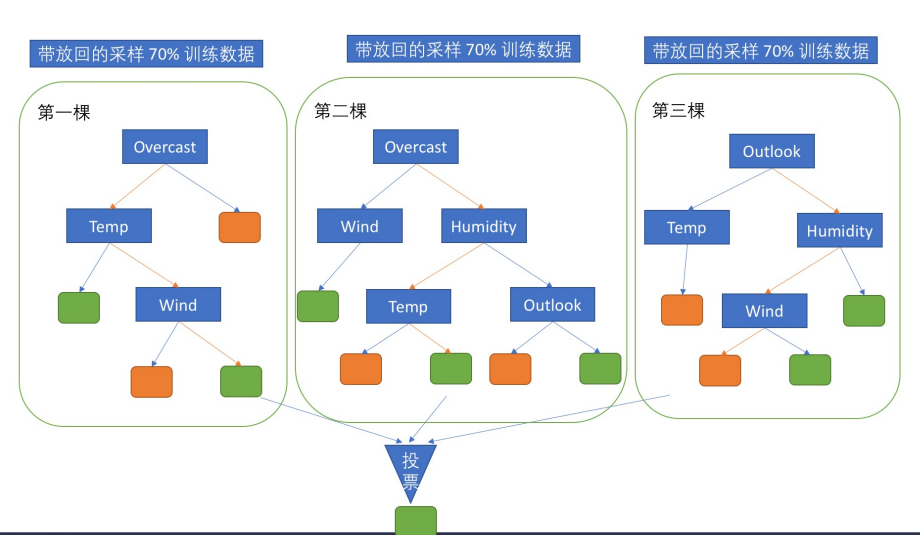
林最重要的就是根据不同的字段的先后决策顺序组成不同的树。
2 XGBoost举例
说实话刚接触XGBoost算法的时候我就蒙了,仔细分析了例子之后就清晰了
2.1 问题和结果
请分析下图示例:
假设我们不知道用户年龄的情况下,通过用户行为来预测用户的年龄
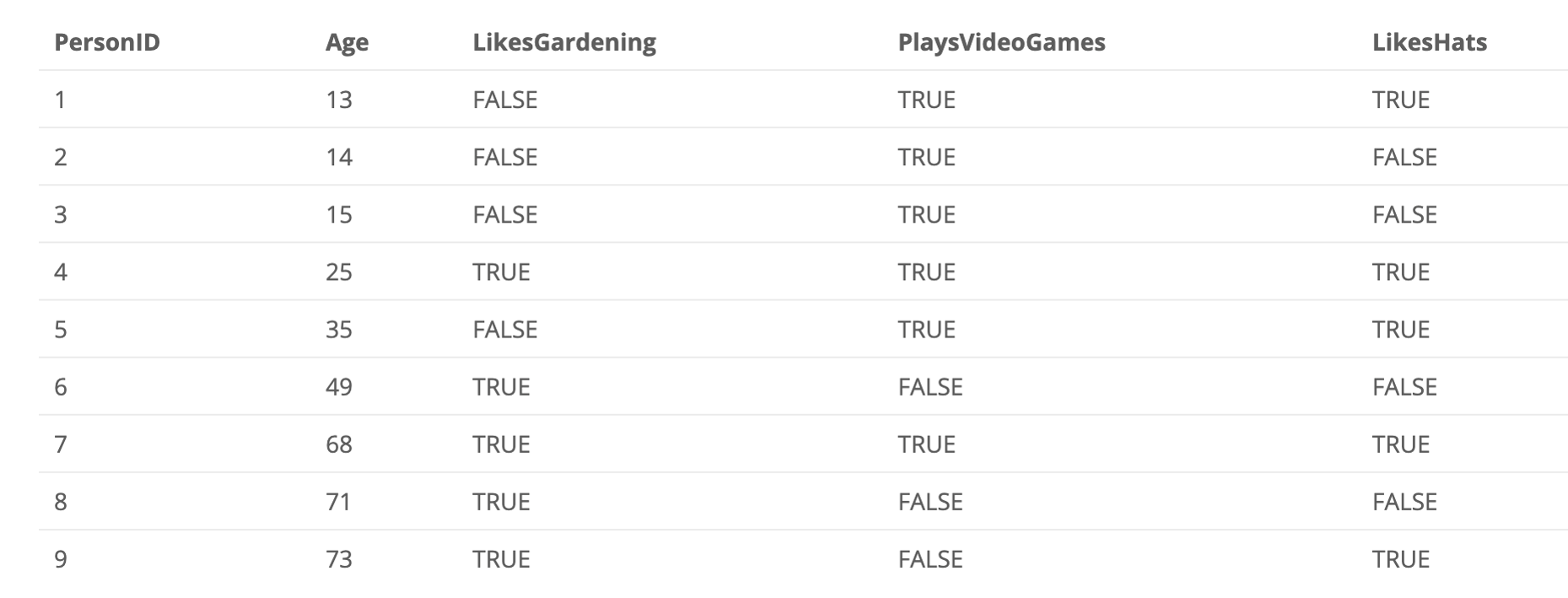
,XGBoost的计算结果如下:

2.2 第一棵树的计算方法

19.25和57.2是怎么来的呢?
$ (13 + 14 + 15 + 35) / 4 = 19.25 $
$ (25 + 49 + 68 + 71 + 73) / 5 = 57.2$
为什么要这么算?因为XGBoost算法就是一个号称"三个臭皮匠,顶个诸葛亮"的算法,其强悍之处在于多棵树计算结果的迭代,所以最初取平均值影响不大。
这里面还有一个残差(residual)的概念,残差 = 实际结果 - 预测结果
比如:Person1的Tree1残差为\(13 - 19.25 = -6.25\)
2.3 第二棵树的计算方法

(https://img2018.cnblogs.com/blog/753880/201908/753880-20190802183318845-666594384.png)
这里要注意是第二棵决策树,并非是第一棵树的一个节点。
第一棵决策树是按LikeGardening来分的,第二棵树是按PlaysVedioGames来分的。
第二棵树的预测结果是怎么算的?
$ 7.133 = (-8.2 + 13.8 + 15.8) / 3 $
$ -3.567 = (-6.25 -5.25 -4.25 -32.2 + 15.75 + 10.08) / 6 $
也就是第二棵树的预测结果是第一棵树残差的平均数。
最终的联合预测结果的计算方法:
比如:Person1的计算方法:
$ 15.683 = 19.25 + (-3.567) $
最新的残差的算法:
$ 2.683 = 15.683 - 13 $
从上面的例子中我们可以看出,实际上问题是由预测年龄转变成了找到最佳的残差值。
这样多棵树就起到了联合学习的效果,残差也会逐渐逼近最终的真实年龄值。
这样做的好处就在于节省了很大的计算量,也因此XGBoost会火。
Bagging:Leverages unstable base learners that are weak because of overfitting
Boosting: Leverage stable base learners that are weak because of underfitting
3 XGBoost公式推导
3.1 第一种理解公式
残差:
\(y_{i,residual} = y_{i,true}-y_{i,predict}\)
预测值:
$ y_{(i,k,predict)} = \frac{1}{m}\sum_{j}^{m} y_{(i,j,k-1)} , y_{(i,0,predict)}=y_{(i,true)} $
其中m就是i所在叶子节点所包含的记录数, 我们求和的就是此叶子节点中每条记录的上一个棵树的预测值。
最终的结果就是把所有的预测值加起来就行了。
3.2 第二种理解公式
这样标达过于麻烦,因此我们换一种简单的方法:
假设训练了K棵树,\(f_{k}(x_{i})\)为第i个人在第k棵树上的预测值(其实这个值就是上面例子中的残差而已),而训练完k棵树的最终预测值是:
\hat{y}{i} = \sum{k=1}^{K}f_{k}(x_{i})
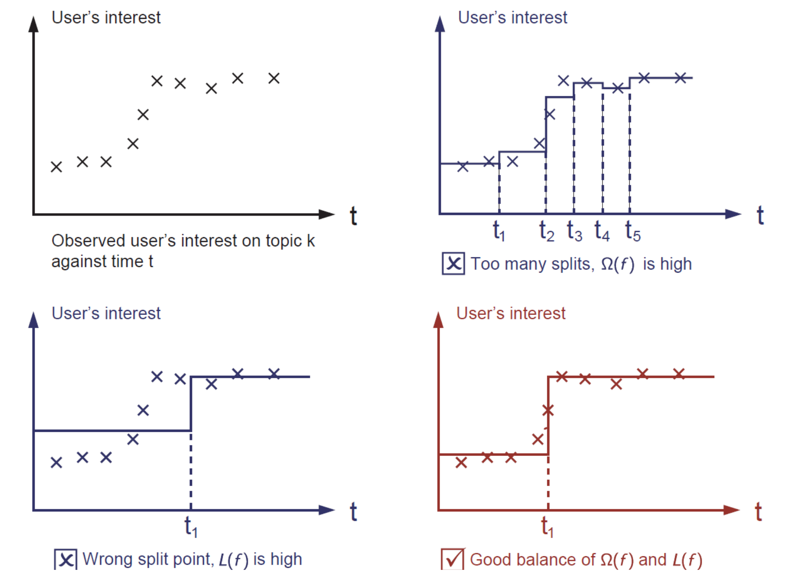
有预测值并不是我们的目标,我们的目标是方差最小,因此目标函数为:

第2节的例子,后面的公式推导就是按部就班地代入就行了。
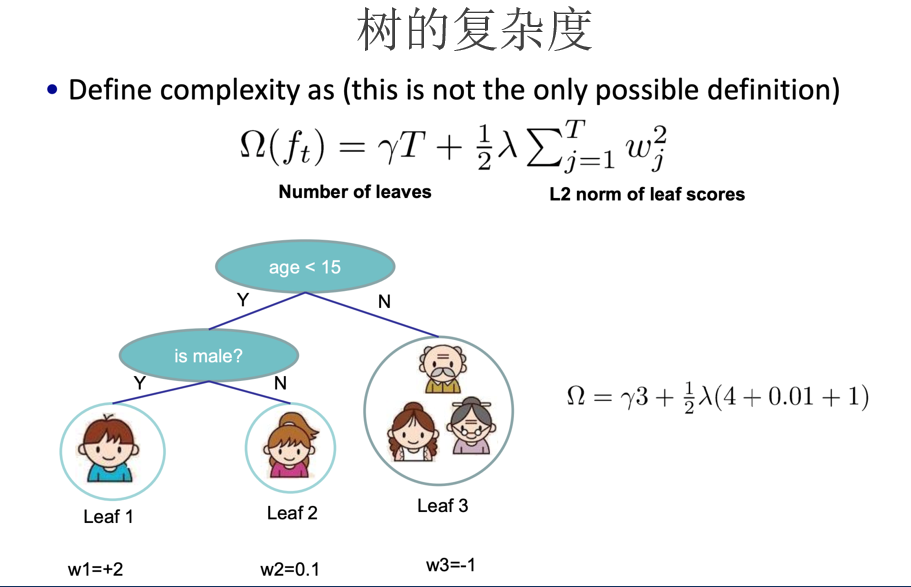
首先将目标函数展开,再封装用泰勒公式模型求导,找出极值点再带回到目标函数求得极值的值,把k个极值加起来作为得分就可以找到最佳的树的分割了。
(后面的部分太麻烦了,就不一一解释了)




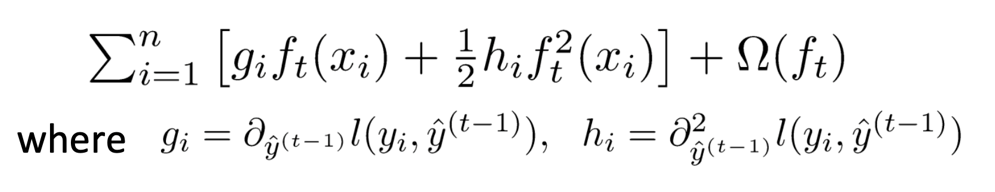







机器学习笔记8:XGBoost的更多相关文章
- Python机器学习笔记:XgBoost算法
前言 1,Xgboost简介 Xgboost是Boosting算法的其中一种,Boosting算法的思想是将许多弱分类器集成在一起,形成一个强分类器.因为Xgboost是一种提升树模型,所以它是将许多 ...
- Python机器学习笔记 集成学习总结
集成学习(Ensemble learning)是使用一系列学习器进行学习,并使用某种规则把各个学习结果进行整合,从而获得比单个学习器显著优越的泛化性能.它不是一种单独的机器学习算法啊,而更像是一种优 ...
- 机器学习笔记:Gradient Descent
机器学习笔记:Gradient Descent http://www.cnblogs.com/uchihaitachi/archive/2012/08/16/2642720.html
- 机器学习笔记5-Tensorflow高级API之tf.estimator
前言 本文接着上一篇继续来聊Tensorflow的接口,上一篇中用较低层的接口实现了线性模型,本篇中将用更高级的API--tf.estimator来改写线性模型. 还记得之前的文章<机器学习笔记 ...
- Python机器学习笔记:使用Keras进行回归预测
Keras是一个深度学习库,包含高效的数字库Theano和TensorFlow.是一个高度模块化的神经网络库,支持CPU和GPU. 本文学习的目的是学习如何加载CSV文件并使其可供Keras使用,如何 ...
- Python机器学习笔记:sklearn库的学习
网上有很多关于sklearn的学习教程,大部分都是简单的讲清楚某一方面,其实最好的教程就是官方文档. 官方文档地址:https://scikit-learn.org/stable/ (可是官方文档非常 ...
- Python机器学习笔记:不得不了解的机器学习面试知识点(1)
机器学习岗位的面试中通常会对一些常见的机器学习算法和思想进行提问,在平时的学习过程中可能对算法的理论,注意点,区别会有一定的认识,但是这些知识可能不系统,在回答的时候未必能在短时间内答出自己的认识,因 ...
- 机器学习笔记(4):多类逻辑回归-使用gluton
接上一篇机器学习笔记(3):多类逻辑回归继续,这次改用gluton来实现关键处理,原文见这里 ,代码如下: import matplotlib.pyplot as plt import mxnet a ...
- 【转】机器学习笔记之(3)——Logistic回归(逻辑斯蒂回归)
原文链接:https://blog.csdn.net/gwplovekimi/article/details/80288964 本博文为逻辑斯特回归的学习笔记.由于仅仅是学习笔记,水平有限,还望广大读 ...
- cs229 斯坦福机器学习笔记(一)-- 入门与LR模型
版权声明:本文为博主原创文章,转载请注明出处. https://blog.csdn.net/Dinosoft/article/details/34960693 前言 说到机器学习,非常多人推荐的学习资 ...
随机推荐
- django中models字段的联合限制
一.字段联合使用的限制设置: 有这么个需求,现有两个字段,A字段是选择用户是不是vip, B字段是统计用户的vip等级; 要求: 用户不是vip时,A选择false,B字段为空; 是vip时,A字段选 ...
- Python 的AES加密与解密
AES加密方式有五种:ECB, CBC, CTR, CFB, OFB 从安全性角度推荐CBC加密方法,本文介绍了CBC,ECB两种加密方法的python实现 python 在 Windows下使用AE ...
- Java代理(静态代理、JDK动态代理、CGLIB动态代理)
Java中代理有静态代理和动态代理.静态代理的代理关系在编译时就确定了,而动态代理的代理关系是在运行期确定的.静态代理实现简单,适合于代理类较少且确定的情况,而动态代理则给我们提供了更大的灵活性. J ...
- 食物链【NOI2001】(信息学奥赛一本通 1390)
[题目描述] 动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形.A吃B, B吃C,C吃A. 现有N个动物,以1-N编号.每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种 ...
- 基于web公交查询系统---搭建mvc连接数据库(我的毕业设计,进度继续)
建立一个spring的项目:我在已经做过的项目基础下做的,所以接口连接数据库挺快. 搭建好的.对应好数据库: 前几天进度已经完成简单的设计: 完成登录,用户管理(修改删除). 继续的数据库的信息获取, ...
- javaWeb项目配置自定义404错误页
1.情景展示 为了隐藏tomcat版本信息以及显示更友好的错误信息提示,如何将404的错误跳转到指定页面? 2.解决方案 第一步:修改项目的web.xml 将如下代码添加到</web-a ...
- UE4命令行参数解析
转自:https://blog.csdn.net/u012999985/article/details/53544389 一 .命令行参数简述命令行参数是一连串的关键字字符串,当运行可执行文件时可以通 ...
- cad.net 2008使用WPF(摘录山人)
由于WPF的优点多多,而且在大量的winform的操作下感觉到数据操作的麻烦....推荐大家看杨中科WPF数据绑定教程 https://www.bilibili.com/video/av3388348 ...
- mysql中,手动提交事务
1: 在mysql中,手动提交事务的案例:CREATE PROCEDURE tfer_funds (from_account int, to_account int, tfer_amoun ...
- 【数据结构与算法】线性表操作(C语言)
#include <stdio.h> #include <stdlib.h> #define OK 1 #define NO 0 #define MAXSIZE 20 type ...
