树剖LCA讲解

LCA的类型多种多样，只说我知道的，就有倍增求LCA，tarjin求LCA和树链剖分求LCA，当然，也还有很多其他的方法。

其中最常用，速度最快的莫过于树链剖分的LCA了。

树链剖分，首先字面理解一下，什么是树链剖分。

　　就是把一棵树剖分为若干条链，然后利用数据结构(树状数组，SBT，Splay，线段树等等)去维护每一

条链，复杂度为O(logn)

　　那么，树链剖分的第一步当然是对整棵树进行遍历，预处理一些要用的变量。

void dfs(int now){

    siz[now]=;

    deep[now]=deep[dad[now]]+;

    for(int i=head[now];i;i=net[i])

        if(to[i]!=dad[now]){

            dad[to[i]]=now;

            dfs(to[i]);

            siz[now]+=siz[to[i]];

        }

}

　　其中dad[i]=j表示节点i的爸爸是j，deep[i]表示节点i的深度，siz[i]表示以节点i为祖先的子树的大小（也就是这个子树里节点的个数）　　

　　第二步就是对树进行轻重边的划分，这样我们就可以保证每一个点属于且只属于一条链。

在这棵树中其实，只有重链是我们用的到的，轻链一般就被忽略了。

　　而我们一般是通过儿子个数的多少来划分出轻重边的，在所有的儿子结点中，各以他们为祖先的子树的节点的个数多的儿子节点与其父亲的连边就是一条重边。这句话有点绕口，看图理解一下：（因为这棵树不一定是二叉树，一个节点可能有多个儿子，这这例子是一个二叉树的，不太全面。）

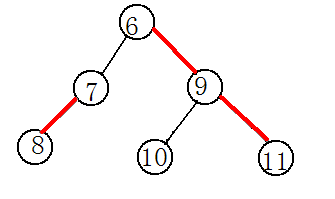
在这个图里面6和9的连边就是一条重边，而6和7的连边就是一条轻边。类似的，9这个节点有两个儿子，以这两个儿子为祖先的子树的大小是相同的，所以随便找一条

边作为重边就可以了,而7只有一个子节点所以7和8的链理所因当就是重链了。

对于这样的一颗树来说，他的轻重链分布如下所示：其中，灰色粗线表示重边，黑色细线表示轻边。

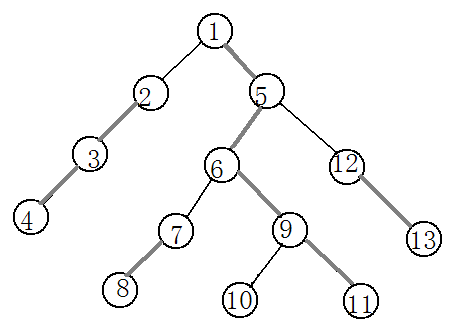
这是他的边的分布情况：

这是找轻重链的代码：其中top[i]表示点i沿他的重边上去，最高能到达的点。

比如上面的图里面每个点的top分别是：1，2，2，2，1，1，7，7，1，10，1，12，12

void dfs1(int x){

    int t=;

    if(!top[x])    top[x]=x;

    for(int i=head[x];i;i=net[i])

        if(to[i]!=dad[x]&&siz[to[i]]>siz[t])

            t=to[i];

    if(t){

        top[t]=top[x];

        dfs1(t);

    }

    for(int i=head[x];i;i=net[i])

        if(to[i]!=dad[x]&&t!=to[i])

            dfs1(to[i]);

}

找完轻重链后，就可以进行下一步操作了，找最近公共祖先。

先看一下代码：

int lca(int x,int y){

    for(;top[x]!=top[y];){

        if(deep[top[x]]<deep[top[y]])

            swap(x,y);

        x=dad[top[x]];

    }

    if(deep[x]>deep[y])

        swap(x,y);

    return x;

}

代码是非常好理解的，就是一个while语句，当两个点位于一条重链上的时候结束操作。

否则的话，深度深的点，顺着他所在的重链向上跳。跳到这条重链的上一个点的位置。在两个点位于一条链上之后，深度浅的点的位置，就是我们要找的公共祖先。

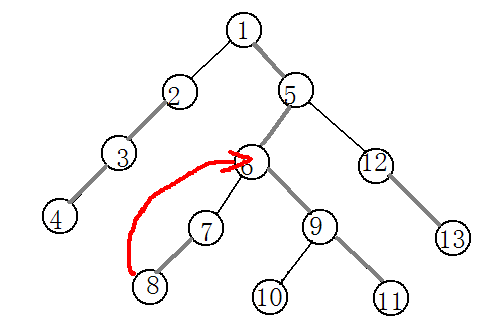
还是这个图，如果要求8和11的最近公共祖先。第一步就是让8顺着边向上跳他会跳到为位置6的点上去，然后6和11位于同一条链上，6的深度浅，6就是我们要求的最近公共祖先。

再举一个复杂点的例子：如果要求10和13的最近公共祖先要怎么呢？

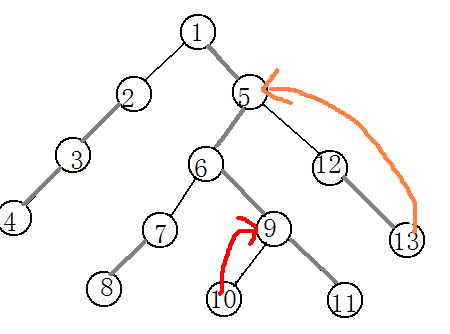
首先，找到两个点中深度较深的点，是10,10号点向上跳，跳到9号点，然后是13号点向上跳，回跳到5号点，这是5和9位于同一条链上，5号点就是我们所求的最近公共祖先。

有人可能会产生这样的问题：我在跳边的时候，为什么要跳到重链顶点的父亲，而不跳到重链顶点，这样万一错过了最近公共祖先肿么办？

　　那就要请你自己好好考虑了，因为这个问题在上面已经回答过了。

第一个问题：如果跳到顶点的话，像是上面的图中的１０号点就跳不动了，那公共祖先就出不来了。

第二个问题：不会。因为除了叶子结点，每一个节点都一定属于一条重链。

答案

例题：P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

#include<cstdio>

#include<cstring>

#include<iostream>

#include<algorithm>

#define MAXN 500010

using namespace std;

int n,m,s,tot;

int to[MAXN*],net[MAXN*],head[MAXN];

int dad[MAXN],deep[MAXN],siz[MAXN],top[MAXN];

void add(int u,int v){

    to[++tot]=v;net[tot]=head[u];head[u]=tot;

    to[++tot]=u;net[tot]=head[v];head[v]=tot;

}

void dfs(int now){

    siz[now]=;

    deep[now]=deep[dad[now]]+;

    for(int i=head[now];i;i=net[i])

        if(to[i]!=dad[now]){

            dad[to[i]]=now;

            dfs(to[i]);

            siz[now]+=siz[to[i]];

        }

}

void dfs1(int x){

    int t=;

    if(!top[x])    top[x]=x;

    for(int i=head[x];i;i=net[i])

        if(to[i]!=dad[x]&&siz[to[i]]>siz[t])

            t=to[i];

    if(t){

        top[t]=top[x];

        dfs1(t);

    }

    for(int i=head[x];i;i=net[i])

        if(to[i]!=dad[x]&&t!=to[i])

            dfs1(to[i]);

}

int lca(int x,int y){

    for(;top[x]!=top[y];){

        if(deep[top[x]]<deep[top[y]])

            swap(x,y);

        x=dad[top[x]];

    }

    if(deep[x]>deep[y])

        swap(x,y);

    return x;

}

int main(){

    scanf("%d%d%d",&n,&m,&s);

    for(int i=;i<n;i++){

        int u,v;

        scanf("%d%d",&u,&v);

        add(u,v);

    }

    dfs(s);

    dfs1(s);

    for(int i=;i<=n;i++)    cout<<top[i]<<" ";

    for(int i=;i<=m;i++){

        int u,v;

        scanf("%d%d",&u,&v);

        cout<<lca(u,v)<<endl;

    }

}

/*

13 1 1

1 2

2 3

3 4

1 5

5 6

6 7

7 8

6 9

9 10

9 11

5 12

12 13

*/

练习题：

codevs 2370 小机房的树

codevs 1036 商务旅行

洛谷 P3398 仓鼠找sugar

HDU 2586 How far away ？

cogs 2478. [HZOI 2016]简单的最近公共祖先

bzoj 3732: Network

洛谷 P2633 Count on a tree

code vs 3305 水果姐逛水果街Ⅱ

洛谷 P3128 [USACO15DEC]最大流Max Flow