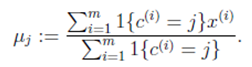k-meas非监督聚类分析

实验名称： k-meas非监督聚类分析

 

一、实验目的和要求

目的：

1. 加深对非监督学习的理解和认识
2. 掌握聚类方法K-Means算法的设计方法

 

要求：

    根据聚类数据，采用k-Means聚类方法画出聚类中心

二、实验环境、内容和方法

环境：windows 7，python2.6 ，Eclipse，Pydev

内容：

1)   非监督学习的理论基础  

2)   动态聚类分析的思想和理论依据 

3)   聚类算法的评价指标

 

三、实验基本原理

K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

我们以一个二维的例子来说明下聚类的目的。如下图左所示，假设我们的n个样本点分布在图中所示的二维空间。从数据点的大致形状可以看出它们大致聚为三个cluster，其中两个紧凑一些，剩下那个松散一些。我们的目的是为这些数据分组，以便能区分出属于不同的簇的数据，如果按照分组给它们标上不同的颜色，就是像下图右边的图那样：

如果人可以看到像上图那样的数据分布，就可以轻松进行聚类。但我们怎么教会计算机按照我们的思维去做同样的事情呢？这里就可以使用k-means算法。

 

 

算法过程如下：

1）从N个文档随机选取K个文档作为质心

2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类

3）重新计算已经得到的各个类的质心

4）迭代2～3步直至新的质心与原质心相等或小于指定阈值，算法结束

具体如下：

输入：k, data[n];

（1） 选择k个初始中心点，例如c[0]=data[0],…c[k-1]=data[k-1]；

（2） 对于data[0]….data[n]，分别与c[0]…c[k-1]比较，假定与c[i]差值最少，就标记为i；

（3） 对于所有标记为i点，重新计算c[i]={ 所有标记为i的data[j]之和}/标记为i的个数；

（4） 重复(2)(3)，直到所有c[i]值的变化小于给定阈值。

 

 

k-means算法是一种很常见的聚类算法，它的基本思想是：通过迭代寻找k个聚类的一种划分方案，使得用这k个聚类的均值来代表相应各类样本时所得的总体误差最小。

k-means算法的基础是最小误差平方和准则。其代价函数是：

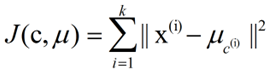
式中，μc(i)表示第i个聚类的均值。我们希望代价函数最小，直观的来说，各类内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。k-means算法是将样本聚类成 k个簇（cluster），其中k是用户给定的，其求解过程非常直观简单，具体算法描述如下：

1、随机选取 k个聚类质心点

2、重复下面过程直到收敛 {

对于每一个样例 i，计算其应该属于的类：

对于每一个类 j，重新计算该类的质心：

}

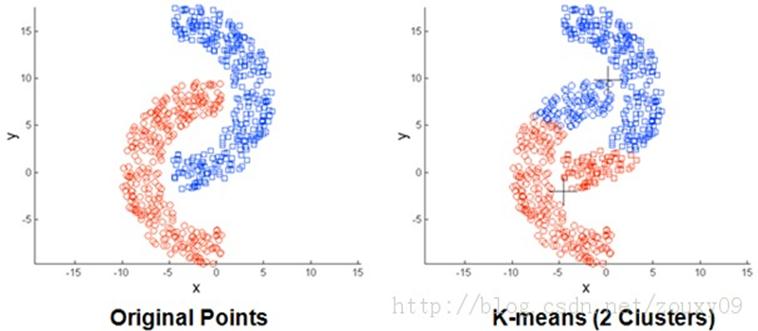
下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

其伪代码如下：

********************************************************************

创建k个点作为初始的质心点（随机选择）

当任意一个点的簇分配结果发生改变时

对数据集中的每一个数据点

对每一个质心

计算质心与数据点的距离

将数据点分配到距离最近的簇

对每一个簇，计算簇中所有点的均值，并将均值作为质心

********************************************************************

 

 

四、实验过程描述

k-means算法比较简单，但也有几个比较大的缺点：

（1）k值的选择是用户指定的，不同的k得到的结果会有挺大的不同，如下图所示，左边是k=3的结果，这个就太稀疏了，蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果，可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的：

（2）对k个初始质心的选择比较敏感，容易陷入局部最小值。例如，我们上面的算法运行的时候，有可能会得到不同的结果，如下面这两种情况。K-means也是收敛了，只是收敛到了局部最小值：

（3）存在局限性，如下面这种非球状的数据分布就搞不定了：

（4）数据库比较大的时候，收敛会比较慢。

k-means老早就出现在江湖了。所以以上的这些不足也被世人的目光敏锐的捕捉到，并融入世人的智慧进行了某种程度上的改良。例如问题（1）对k的选择可以先用一些算法分析数据的分布，如重心和密度等，然后选择合适的k。而对问题（2），有人提出了另一个成为二分k均值（bisecting k-means）算法，它对初始的k个质心的选择就不太敏感。

 

五、实验结果

 

六、附录代码

：

 

Kmeans.py:

 

from numpy import *

import time

import matplotlib.pyplot as plt

 

 

# calculate Euclidean distance

def
euclDistance(vector1, vector2):

    return sqrt(sum(power(vector2 - vector1, 2)))

 

# init centroids with random samples

def
initCentroids(dataSet, k):

    numSamples, dim = dataSet.shape

    centroids = zeros((k, dim))

    for i in range(k):

        index = int(random.uniform(0, numSamples))

        centroids[i, :] = dataSet[index, :]

    return centroids

 

# k-means cluster

def
kmeans(dataSet, k):

    numSamples = dataSet.shape[0]

    # first column stores which cluster this sample belongs to,

    # second column stores the error between this sample and its centroid

    clusterAssment = mat(zeros((numSamples, 2)))

    clusterChanged = True

 

    ## step 1: init centroids

    centroids = initCentroids(dataSet, k)

 

    while clusterChanged:

        clusterChanged = False

        ## for each sample

        for i in xrange(numSamples):

            minDist = 100000.0

            ## for each centroid

            ## step 2: find the centroid who is closest

            for j in range(k):

                distance = euclDistance(centroids[j, :], dataSet[i, :])

                if distance < minDist:

                    minDist = distance

                    minIndex = j

            

            ## step 3: update its cluster

            if clusterAssment[i, 0] != minIndex:

                clusterChanged = True

 

        ## step 4: update centroids

        for j in range(k):

            pointsInCluster = dataSet[nonzero(clusterAssment[:, 0].A == j)[0]]

            centroids[j, :] = mean(pointsInCluster, axis = 0)

 

    print
'Congratulations, cluster complete!'

    return centroids, clusterAssment

 

# show your cluster only available with 2-D data

def
showCluster(dataSet, k, centroids, clusterAssment):

    numSamples, dim = dataSet.shape

    if dim != 2:

        print
"Sorry! I can not draw because the dimension of your data is not 2!"

        return

 

    mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']

    if k > len(mark):

        print
"Sorry! Your k is too large! please contact Zouxy"

        return

 

    # draw all samples

    for i in xrange(numSamples):

        markIndex = int(clusterAssment[i, 0])

        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])

 

    mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']

    # draw the centroids

    for i in range(k):

        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize = 12)

 

    plt.show()

    
 

    
 

    
 

    
 

    
 

    
 

    
 

 

 

Test_kmeans.py:

 

 

from numpy import *

import time

import matplotlib.pyplot as plt

 

import kmeans

 

from kmeans import kmeans,showCluster

 

## step 1: load data

print
"step 1: load data..."

dataSet = []

fileIn = open('F:\code\python\k-means-2014-5-8/testSet.txt')

for line in fileIn.readlines():

    lineArr = line.strip().split('\t')

    dataSet.append([float(lineArr[0]), float(lineArr[1])])

 

## step 2: clustering...

print
"step 2: clustering..."

dataSet = mat(dataSet)

centroids, clusterAssment = kmeans(dataSet, k)

 

## step 3: show the result

print
"step 3: show the result..."

showCluster(dataSet, k, centroids, clusterAssment)

 

 

数据点：testSet.txt

1.658985    4.285136

-3.453687    3.424321

4.838138    -1.151539

-5.379713    -3.362104

0.972564    2.924086

-3.567919    1.531611

0.450614    -3.302219

-3.487105    -1.724432

2.668759    1.594842

-3.156485    3.191137

3.165506    -3.999838

-2.786837    -3.099354

4.208187    2.984927

-2.123337    2.943366

0.704199    -0.479481

-0.392370    -3.963704

2.831667    1.574018

-0.790153    3.343144

2.943496    -3.357075

-3.195883    -2.283926

2.336445    2.875106

-1.786345    2.554248

2.190101    -1.906020

-3.403367    -2.778288

1.778124    3.880832

-1.688346    2.230267

2.592976    -2.054368

-4.007257    -3.207066

2.257734    3.387564

-2.679011    0.785119

0.939512    -4.023563

-3.674424    -2.261084

2.046259    2.735279

-3.189470    1.780269

4.372646    -0.822248

-2.579316    -3.497576

1.889034    5.190400

-0.798747    2.185588

2.836520    -2.658556

-3.837877    -3.253815

2.096701    3.886007

-2.709034    2.923887

3.367037    -3.184789

-2.121479    -4.232586

2.329546    3.179764

-3.284816    3.273099

3.091414    -3.815232

-3.762093    -2.432191

3.542056    2.778832

-1.736822    4.241041

2.127073    -2.983680

-4.323818    -3.938116

3.792121    5.135768

-4.786473    3.358547

2.624081    -3.260715

-4.009299    -2.978115

2.493525    1.963710

-2.513661    2.642162

1.864375    -3.176309

-3.171184    -3.572452

2.894220    2.489128

-2.562539    2.884438

3.491078    -3.947487

-2.565729    -2.012114

3.332948    3.983102

-1.616805    3.573188

2.280615    -2.559444

-2.651229    -3.103198

2.321395    3.154987

-1.685703    2.939697

3.031012    -3.620252

-4.599622    -2.185829

4.196223    1.126677

-2.133863    3.093686

4.668892    -2.562705

-2.793241    -2.149706

2.884105    3.043438

-2.967647    2.848696

4.479332    -1.764772

-4.905566    -2.911070