OpenCascade Sweep Algorithm

Abstract. Sweeps are the objects you obtain by sweeping a profile along a path. Sweep is a very useful modeling algorithm. The paper focus on the introduction of the sweep algorithms in the opencascade.

Key Words. Sweep, Prism, Revol, Pipe, Frenet Trihedron,

1. Introduction

随着计算机技术的发展和普及，计算机辅助设计与制造（CAD/CAM）技术也得到了迅猛发展，它们推动许多领域的设计革命，计算机辅助设计与制造技术的发展和应用水平已经成为衡量一个国家现代化水平的重要标志之一。

最近中兴事件在国内引起了大家的广泛讨论，由于目前国内还制造不出能替代的芯片，所以可以从中找到与发达国家之间的差距，其实在CAD领域又何尝不是这样呢？不过在通用CAD方面，国内有一些软件厂家，有替代产品。而在行业CAD方面，一直是国外软件的天下。

原来国内有些声音是“造不如买，买不如租”，引进了许多国外软件。这些国外软件是很优秀，极大地提高了生产力。如果一直买，不思进取，结果应该会像中兴一样。如果自己造，刚开始是需要投入很大的成本，但是后面优势是不言而喻的。

国际上的三维内核目前功能相对齐全，开源的只有OpenCASCADE。国内的相关内核只从《计算机图形学》的书上见过，没有看过实物。还有一些软件厂商收购的国外内核。开源的OpenCASCADE用来学习造型相关算法还是很不错的。通过学习源码，不仅可以知其然，还可以做到知其所以然。

本文主要对OpenCASCADE中的Sweep扫掠算法的用法进行介绍，先会正确使用。正确使用是研究其实现原理的基础。

扫掠算法是图形学中很常见的造型算法，就是将指定的轮廓Profile沿着一条路径Path扫掠来得到模型。点扫掠得到边；边扫掠得到面；面扫掠得到体。

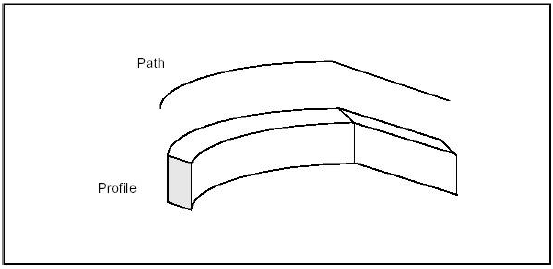
Figure 1. Generating a sweep

类BRepPrimAPI_MakeSweep是扫掠算法的基类，如下图所示：

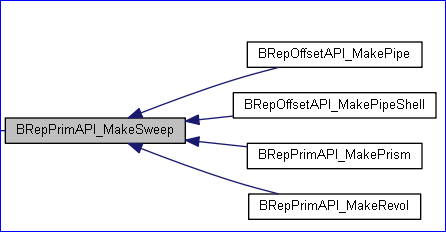
从其派生的几个类分别用于：

l BRepPrimAPI_MakePrism：生成线性扫掠；

l BRepPrimAPI_MakeRevol：生成旋转扫掠；

l BRepOffsetAPI_MakePipeShell：生成通用的扫掠；

下面对这几种情况分别进行说明。

2.Prism

通过类BRepPrimAPI_MakePrism可以创建线性扫掠，也就是拉伸体。在Draw Test Harness中可以使用命令prism来创建拉伸体。

polyline p                

prism r p   

vdisplay p r

在Draw Test Harness中运行上述命令，可以得到一个线性拉伸体，如下图所示：

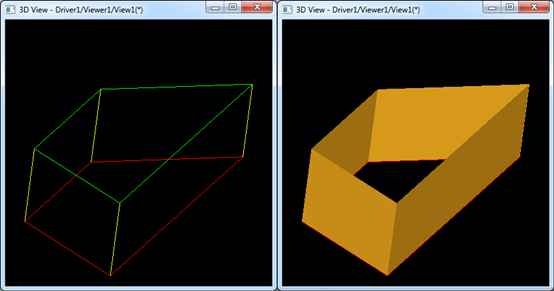
其中红色为轮廓Profile，经过线性扫掠得到右边所示的拉伸体。

3.Revol

通过类BRepPrimAPI_MakeRevol可以创建旋转扫掠，也就是旋转体。在Draw Test Harness中可以使用命令revol来创建旋转体。

polyline p                

revol r p       

vdisplay p r

在Draw Test Harness中运行上述命令，可以得到一个旋转体，如下图所示：

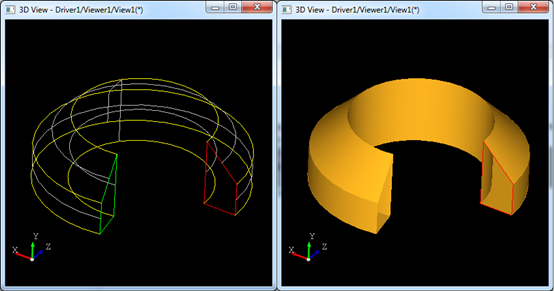
其中红色为轮廓Profile，经过旋转扫掠得到右边所示的旋转体。

4.Pipe Shell

通用的扫掠算法使用类BRepOffAPI_MakePipeShell，在Draw Test Harness中使用如下命令：

l mksweep

l addsweep

l deletesweep

l sestsweep

l buildsweep

其中setsweep命令有如下选项：

setsweep options [arg1 [arg2 [...]]] : options are :

   -FR : Tangent and Normal are given by Frenet trihedron

   -CF : Tangente is given by Frenet, the Normal is computed to minimize the torsion

   -DT : discrete trihedron

   -DX Surf : Tangent and Normal are given by Darboux trihedron,

       Surf have to be a shell or a face

   -CN dx dy dz : BiNormal is given by dx dy dz

   -FX Tx Ty TZ [Nx Ny Nz] : Tangent and Normal are fixed

   -G guide  |(Plan|ACR)  ||(no contact|contact|contact on border) : with guide

-FR选项：切矢和法向由Frenet标架确定；

-CF选项：切矢由Frenet标架指定，法向通过计算最小扭转来确定；

-DT选项：切矢和法向由Darboux标架确定；

-CN选项：副法向由指定的dx, dy, dz确定；

-FT：切矢和法向是固定的；

下面通过例子来说明setsweep中这些标架选项的原理。

polyline p             

circle c       0.2

mkedge e c

wire w e

mksweep p

addsweep w

setsweep -FX   

buildsweep r -C

vdisplay p w r

运行上述Draw Test Harness脚本得到如下图所示模型：

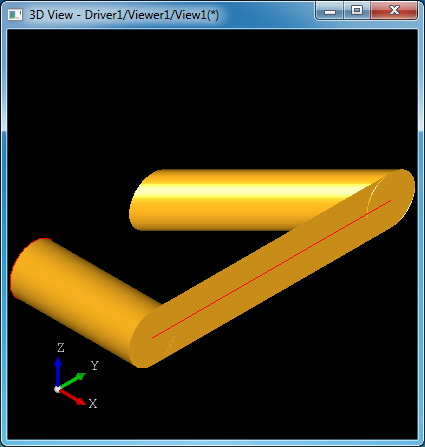
通过setsweep -FX 1 0 0 使轮廓Profile沿着扫掠路径Path移动时，法向始终为X轴方向。

将setsweep设置为FR，即使Profile沿着Path移动时采用Frenet标架，更改后的脚本如下：

mksweep p

addsweep w

setsweep -FR

buildsweep r -C

vdisplay p w r

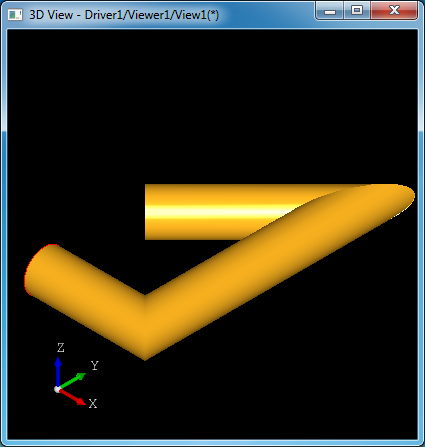
由上图可以看出，轮廓Profile沿着路径Path移动时，轮廓的法向始终与路径平行，即与路径的切线一致。

通过上面命令的对比可以理解setsweep中的选项原理了。关于更多形式的标架，如Darboux标架之类的，可以自己搜索学习。

其中buildsweep命令有如下选项：

buildsweep result [-M/-C/-R] [-S] [tol] : options are

   -M : Discontinuities are treated by Modfication of

        the sweeping mode : it is the default

   -C : Discontinuities are treated like Right Corner

        Treatement is Extent && Intersect

   -R : Discontinuities are treated like Round Corner

        Treatement is Intersect and Fill

   -S : To build a Solid

buildsweep有指定不连续的处理方式及是否生成实体。其中

n -C：将路径Path中不连续的地方通过延长和相交进行处理；

n -R：将路径Path中不连续的地方通过相交和填充进行处理；

下面通过例子来说明buildsweep中选项的用法。通过运行下面的Draw 脚本：

polyline p                

circle c       0.2

mkedge e c

wire w e

mksweep p

addsweep w

buildsweep r -C

vdisplay p w r

在buildsweep时使用－C选项，得到效果如下图所示：

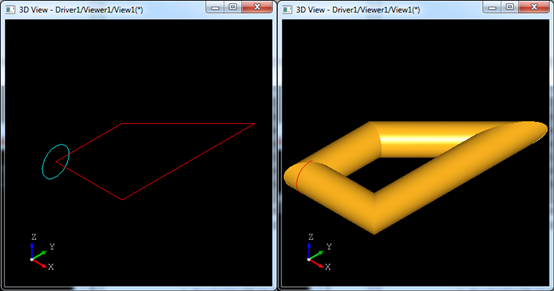
将上述脚本中更改一下buildsweep的选项，由－C改为－R，即：

buildsweep r -R

得到的效果如下图所示：

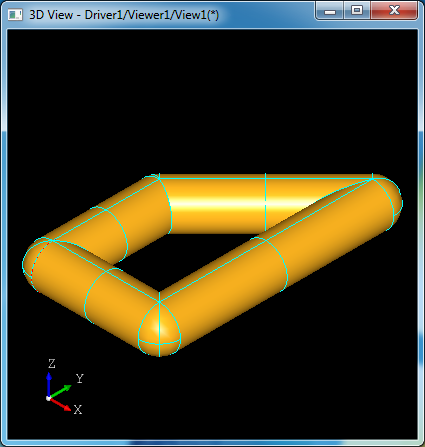
由上面两个结果对比可以理解buildsweep的-C和-R选项了。

5.Conclusion

OpenCASCADE提供了扫掠造型的算法。对于扫掠造型的两个特例Prism和Revol，提供了类BrepPrimAPI_MakePrism和BRepPrimAPI_MakeRevol来分别生成拉伸体和和旋转体。

对于通用的扫掠造型算法，提供了类BRepOffsetAPI_MakePipeShell来生成。使用这个类的时候需要注意轮廓Profile在扫掠路径Path上的标架及扫掠路径曲线不连续的处理。

6.References

1. OpenCASCADE Modeling Algorithms.

2. 詹海生. 李光鑫. 马志欣. 基于ACIS的几何造型技术与系统开发. 清华大学出版社. 2002

3. 陈维桓. 微分几何. 北京大学出版社.