[arc076e]connected?

题意：

给出一个$R\times C$的棋盘，其中$1$到$N$之间的每个正整数都会在棋盘上出现两次，第$i$个数出现的位置是$(X_{i,1},Y_{i,1})$和$(X_{i,2},Y_{i,2})$，现在目的是把每一对相同的数用线（粗细忽略不计）连起来，且线不能相交也不能越过棋盘边界，求是否能完成。

$1\leq R,C\leq 10^8$

$1\leq N\leq 10^5$

题解：

看上去是神仙题，实际上很假。。。

大家有没有玩过麻将连连看那种小游戏？题意中的连线意义就差不多。首先如果把这个棋盘扩展到无限大，即没有棋盘边界的限制，显然一定能满足条件。因为棋盘边上的数字连的线肯定可以在向外连足够远之后连回来，而内部的线由于可以跨越每个格子的边界，必定可以满足条件。（正确性感性理解一下？）

那么有了边界限制之后，就只用考虑在两个位置都在边界上的那些数字，把这些数字看成一对括号，如果整个边界上按顺序（顺时针或逆时针）能构成一个合法括号序列，那么就能满足，否则就不行。画个图感受一下：

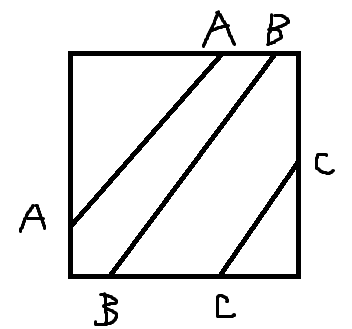
如图，左图是非法的而右图是合法的。那这个东西直接用栈判断一下就好了。。。先把所有位置排序，然后如果现在位置的数字和栈顶相等则弹出栈顶，否则把当前数字压入栈，最后判断栈是否为空即可。

ps：这题细节极其恶心！写挂了五六次才过样例。。。（可能是我写法比较挫）

代码：

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<queue>
 #include<stack>
 #define inf 2147483647
 #define eps 1e-9
 using namespace std;
 typedef long long ll;
 struct node{
     int x,id;
 }li[][];
 int r,c,n,x,y,xx,yy,nw,tot[];
 stack<int>st;
 bool cmp1(node a,node b){
     return a.x<b.x;
 }
 bool cmp2(node a,node b){
     return a.x>b.x;
 }
 int main(){
     scanf("%d%d%d",&r,&c,&n);
     for(int i=;i<=n;i++){
         scanf("%d%d%d%d",&x,&y,&xx,&yy);
         if((x&&y&&x!=r&&y!=c)||(xx&&yy&&xx!=r&&yy!=c))continue;
         if(!x)nw=;
         else if(x==r)nw=;
         else if(!y)nw=;
         else if(y==c)nw=;
         if(nw==||nw==)li[nw][++tot[nw]]=(node){y,i};
         else li[nw][++tot[nw]]=(node){x,i};
         if(!xx)nw=;
         else if(xx==r)nw=;
         else if(!yy)nw=;
         else if(yy==c)nw=;
         if(nw==||nw==)li[nw][++tot[nw]]=(node){yy,i};
         else li[nw][++tot[nw]]=(node){xx,i};
     }
     for(int i=;i<;i++){
         if(i==||i==)sort(li[i]+,li[i]+tot[i]+,cmp1);
         else sort(li[i]+,li[i]+tot[i]+,cmp2);
         for(int j=;j<=tot[i];j++){
             if(!st.empty()&&li[i][j].id==st.top())st.pop();
             else st.push(li[i][j].id);
         }
     }
     if(st.empty())puts("YES");
     else puts("NO");
     return ;
 }