【译】第37节---EF6-异步查询和保存
原文:http://www.entityframeworktutorial.net/entityframework6/async-query-and-save.aspx
你可以在.NET4.5下使用 EF6 DbContext异步执行查询和命令。
我们来看看如何先执行异步查询,然后再看对context.SaveChanges的异步调用。
异步查询
private static async Task<Student> GetStudent()
{
Student myStudent = null; using (var context = new SchoolDBEntities())
{
Console.WriteLine("Start GetStudent..."); myStudent = await (context.Students.Where(s => s.StudentID == ).FirstOrDefaultAsync<Student>()); Console.WriteLine("Finished GetStudent..."); } return student;
}
上面的代码所示,GetStudent方法使用async关键字标识使其异步。
异步方法的返回类型必须为Task。
GetStudent返回一个Student实体的对象,所以返回类型必须是Task <Student>。
此外,查询标记为await。 这将释放调用线程以执行其他操作,直到它执行查询并返回数据。
我们使用了System.Data.Entity的FirstOrDefaultAsync扩展方法,你也可以适当使用其他扩展方法,例如SingleOrDefaultAsync,ToListAsyn等。
异步保存
可以和上面示例一样的方式异步调用context.SaveChanges:
private static async Task SaveStudent(Student editedStudent)
{ using (var context = new SchoolDBEntities())
{
context.Entry(editedStudent).State = EntityState.Modified; Console.WriteLine("Start SaveStudent..."); int x = await (context.SaveChangesAsync()); Console.WriteLine("Finished SaveStudent...");
} }
获取异步查询的结果
异步时可以使用wait方法得到结果,如下:
public static void AsyncQueryAndSave()
{
var queryResult = GetStudent(); Console.WriteLine("Let's do something else till we get student.."); queryResult.Wait(); var student1 = queryResult.Result; student1.FirstName = "Modified First Name"; var studentSave = SaveStudent(student1); Console.WriteLine("Let's do something else till we save student.." ); studentSave.Wait(); }
如上面的代码所示,我们以普通的方式调用Async方法GetStudent,并将引用存储在变量学生中。
然后,我们调用student.wait()。
这意味着调用线程应该等待直到异步方法完成,所以我们可以执行另一个进程,直到我们从异步方法得到结果。
上面显示的代码将具有以下输出:
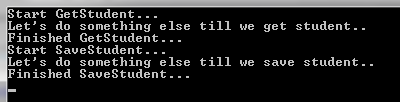
【译】第37节---EF6-异步查询和保存的更多相关文章
- Entity Framework异步查询和保存
EF6开始提供了通过async和await关键字实现异步查询和保存的支持(.net 4.5及更高版本).虽然不是所有的操作都能从异步中获益,但是耗时的操作.网络或IO密集型任务中,使用异步可以提升客户 ...
- 《Entity Framework 6 Recipes》中文翻译系列 (41) ------ 第七章 使用对象服务之标识关系中使用依赖实体与异步查询保存
翻译的初衷以及为什么选择<Entity Framework 6 Recipes>来学习,请看本系列开篇 7-7 标识关系中使用依赖实体 问题 你想在标识关系中插入,更新和删除一个依赖实体 ...
- Entity Framework入门教程(11)---EF6中的异步查询和异步保存
EF6中的异步查询和异步保存 在.NET4.5中介绍了异步操作,异步操作在EF中也很有用,在EF6中我们可以使用DbContext的实例进行异步查询和异步保存. 1.异步查询 下边是一个通过L2E语法 ...
- php中mysql数据库异步查询实现
问题 通常一个web应用的性能瓶颈在数据库.因为,通常情况下php中mysql查询是串行的.也就是说,如果指定两条sql语句时,第二条sql语句会等到第一条sql语句执行完毕再去执行.这个时候,如果执 ...
- 《Entity Framework 6 Recipes》中文翻译系列 (11) -----第三章 查询之异步查询
翻译的初衷以及为什么选择<Entity Framework 6 Recipes>来学习,请看本系列开篇 第三章 查询 前一章,我们展示了常见数据库场景的建模方式,本章将向你展示如何查询实体 ...
- MSSQL数据库链接字符串Asynchronous Processing=true不是异步查询吗,怎么是缓存
;Asynchronous Processing=true 不是异步查询吗,怎么是缓存 <!--<add name="default" providerName=&q ...
- asp.net mvc异步查询
对于asp.net mvc异步查询 如何做MVC异步查询,做列表页面. 查询是项目中必不可少的工作,而且不同的项目不同的团队,都有自己的简单方法.Asp.net mvc 有自己独特的优势,下面是结合m ...
- Android 异步查询框架AsyncQueryHandler的使用
AsyncQueryHandler简介: 异步的查询操作帮助类,可以处理增删改(ContentProvider提供的数据) 使用场景: 在一般的应用中可以使用ContentProvider去操作数据库 ...
- 异步查询json传日期格式到前台,变成了时间戳的格式
问题: 使用mybatis 查询mysql数据库,其中一个日期格式的字段,由异步查询使用 json传递到前台,变成了时间戳,而不是日期格式了.如何使查询出的日期展示成日期格式呢 解决办法: 1.尝试使 ...
随机推荐
- HOG基本原理
图像识别,图像预处理,HOG算法介绍. 转自: https://blog.csdn.net/gy429476195/article/details/50156813
- Linux环境变量和本地变量
每一种编程语言中,我们都会碰到变量的作用域的问题.(比如在函数中定义的变量在函数外不能使用的) BASH 中也有类似的问题,局部变量和环境变量(全局变量). 局部变量是普通的变量,仅在创建它的Shel ...
- 【封装函数】当前元素距离html文档顶部距离
function getPositionTop(node) { var top = node.offsetTop; var parent = node.offsetParent; while(pare ...
- python里面的xlrd模块
♦python操作excel主要用到xlrd和xlwt这两个库,即xlrd是读excel,xlwt是写excel的库. 今天就先来说一下xlrd模块: 一.安装xlrd模块 ♦ 到python官网下载 ...
- 详解:PHP加速器配置神器opcache
什么是opcode? 当解释器完成对脚本代码的分析后,便将它们生成可以直接运行的中间代码,也称为操作码(Operate Code,opcode).Opcode cache的目地是避免重复编译,减少CP ...
- 为什么要使用yocto
作为灵活多变且经济高效的解决方案,嵌入式 Linux展现了巨大的价值,并广泛应用于消费电子设备.网络设备.零售点和行业应用程序.然而,广泛的应用也意味着多样化的业务需求,嵌入式解决方案开发人员必须构建 ...
- 纯CSS打造萌萌哒大白
HTML部分: <body> <div id="baymax"> <!-- 定义头部,包括两个眼睛.嘴 --> <div id=" ...
- 使用dockerfile构建自己的镜像
CentOS Linux release 7.2.1511 Docker version 17.03.1-ce 首先应该了解docker镜像的分层机制,这个网上文章很多,简单说就是对镜像的每次修改都是 ...
- 【题解】Luogu P2522 [HAOI2011]Problem b
原题传送门 这题需要运用莫比乌斯反演(懵逼钨丝繁衍) 我们看题面,让求对于区间\([a,b]\)内的整数x和\([c,d]\)内的y,满足$ gcd(x,y)=k$的数对的个数 我们珂以跟容斥原理(二 ...
- 一个简单的购物金额结算(JAVA)
我编写的代码: import java.util.Scanner; public class ZuoYe01 { public static void main(String[] args) { // ...
