内部排序->基数排序->链式基数排序

文字描述

　　基数排序是和前面各类排序方法完全不相同，前面几篇文章介绍的排序算法的实现主要是通过关键字间的比较和移动记录这两种操作，而实现基数排序不需要进行记录关键字间的比较。基数排序是一种借助多关键字排序的思想对单逻辑关键字进行排序的方法。先介绍下什么是多关键字排序，以引入链式基数排序算法。

　　先介绍什么是多关键字排序：

　　比如，对扑克牌进行排序，每张扑克牌有两个“关键字”：花色(梅花<方块<红桃<黑桃)和面值(2<3<,…,A)，且“花色”的地位高于”面值”， 那么对扑克牌排序有两种方法：

　　方法1：先按不同“花色”分成有次序的4堆，每一堆的”花色”相同; 然后分别对每一堆内部按”面值”大小整理有序。这种先对主键字字进行排序，再对次关键字排序的方法叫最高位优先法(简称MSD: Most Significant first)

　　方法2：先按不同”面值”分成13堆，然后将13堆自小到大叠在一起(“3”在”2”之上，”4”在”3”之上,…,最上面的是4张”A”)，然后将这幅牌整个颠倒过来再重新按不同花色分成4堆，最后将这4堆按自小到的次序合在一起(梅花在最下面，黑桃在最上面)。这种先对次键字字进行排序，再对主关键字排序的方法叫最低位优先法(简称LSD: Least Significant first)

　　采用第二种方法LSD法对多关键字进行排序时，也可以不采用之前介绍的各种通过关键字间的比较来实现排序的方法，而是通过若干次“分配”和“收集”来实现排序。

　　关于链式基数排序的介绍：

　　采用多关键字排序中的LSD方法，先对低优先级关键字排序，再按照高点的优先级关键字排序，不过基数排序在排序过程中不需要经过关键字的比较，而是借助“分配”和“收集”两种操作对单逻辑关键字进行排序的一种内部排序方法。

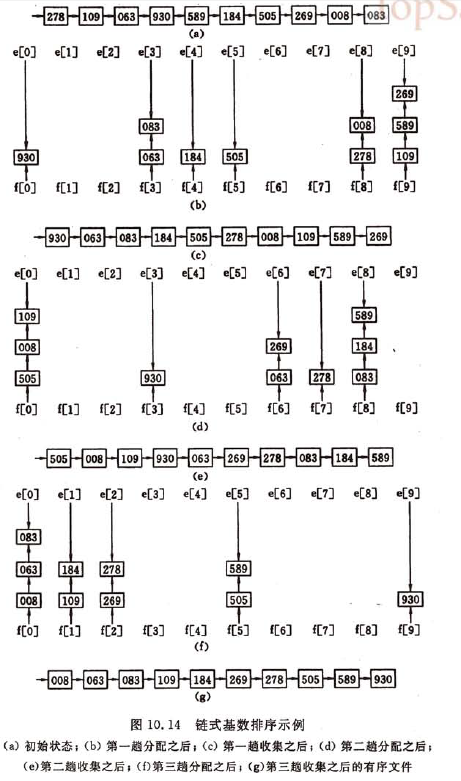
　　比如，若关键字是十进制表示的数字，且范围在[0，999]内，则可以把每一个十进制数字看成由三个关键字组成(K0, K1, K2)，其中K0是百位数，K1是十位数，K2是个位数。基RADIX的取值为10； 按LSD进行排序，从最低位关键字起，按关键字的不同值将序列中记录“分配”到RADIX个队列中后再“收集”之，如此重复d次。按这种方法实现的排序称之为基数排序，以链表作存储结构的基数排序叫链式基数排序。

示意图

算法分析

　　对n个记录(假设每个记录含d个关键字，每个关键字的取值范围为rd个值)进行链式基数排序的时间复杂度为d*(n+rd)，其中每一躺分配的时间复杂度为n，每一躺收集的时间复杂度为rd，整个排序需进行d躺分配和收集。

　　所需辅助空间为2*rd个队列指针，由于采用链表作存储结构，相对于其他采用顺序存储结构的排序方法而言，还增加了n个指针域的空间。

　　链式基数排序是稳定的排序。

代码实现

 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define DEBUG

 #define EQ(a, b) ((a) == (b))
 #define LT(a, b) ((a) <  (b))
 #define LQ(a, b) ((a) <= (b))

 //关键字项数的最大个数
 #define MAX_NUM_OF_KEY    8
 //关键字基数，此时是十进制整数的基数就是10
 #define RADIX            10
 //静态链表的最大长度
 #define MAX_SPACE        10000

 //定义结点中的关键字类型为int
 typedef int KeyType;
 //定义结点中除关键字外的附件信息为char
 typedef char InfoType;

 //静态链表的结点类型
 typedef struct{
     //关键字
     KeyType    keys[MAX_NUM_OF_KEY];
     //除关键字外的其他数据项
     InfoType otheritems;
     int next;
 }SLCell;

 //静态链表类型
 typedef struct{
     //静态链表的可利用空间，r[0]为头结点
     SLCell r[MAX_SPACE];
     //每个记录的关键字个数
     int keynum;
     //静态链表的当前长度
     int recnum;
 }SLList;

 //指针数组类型
 typedef int ArrType[RADIX];

 void PrintSList(SLList L)
 {
     int i = ;
     printf("下标值 ");
     for(i=; i<=L.recnum; i++){
         printf(" %-6d", i);
     }
     printf("\n关键字 ");
     for(i=; i<=L.recnum; i++){
         printf(" %-1d%-1d%-1d,%-2c", L.r[i].keys[], L.r[i].keys[], L.r[i].keys[], L.r[i].otheritems);
     }
 //    printf("\n其他值 ");
 //    for(i=0; i<=L.recnum; i++){
 //        printf(" %-5c", L.r[i].otheritems);
 //    }
     printf("\n下一项 ");
     for(i=; i<=L.recnum; i++){
         printf(" %-6d", L.r[i].next);
     }
     printf("\n");
     return;
 }

 void PrintArr(ArrType arr, int size)
 {
     int i = ;
     for(i=; i<size; i++){
         printf("[%d]%-2d ", i, arr[i]);
     }
     printf("\n");
 }

 /*
  *静态链表L的r域中记录已按(key[0],...,key[i-1])有序
  *本算法按第i个关键字keys[i]建立RADIX个子表，使同一子表中记录的keys[i]相同。
  *f[0,...,RADIX-1]和e[0,...,RADIX-1]分别指向各子表中的第一个记录和最后一个记录。
  */
 void Distribute(SLCell *r, int i, ArrType f, ArrType e)
 {
     int j = ;
     //各子表初始化为空
     for(j=; j<RADIX; j++)
         f[j] = e[j] = ;

     int p = ;
     for(p=r[].next; p; p=r[p].next){
         j = r[p].keys[i];
         if(!f[j])
             f[j] = p;
         else
             r[e[j]].next = p;
         //将p所指的结点插入第j个字表中
         e[j] = p;
     }
 }

 /*
  * 本算法按keys[i]自小到大地将f[0,...,RADIX-1]所指各子表依次链接成一个链表
  * e[0,...,RADIX-1]为各子表的尾指针
  */
 void Collect(SLCell *r, int i, ArrType f, ArrType e){
     int j = , t = ;
     //找到第一个非空子表，
     for(j=; !f[j]; j++);
     //r[0].next指向第一个非空子表的第一个结点
     r[].next = f[j];
     //t指向第一个非空子表的最后结点
     t = e[j];
     while(j<RADIX){
         //找下一个非空子表
         for(j+=; !f[j]; j++);
         //链接两个非空子表
         if(j<RADIX && f[j]){
             r[t].next = f[j];
             t = e[j];
         }
     }
     //t指向最后一个非空子表中的最后一个结点
     r[t].next = ;
 }

 /*
  * L是采用静态链表表示的顺序表。
  * 对L作基数排序，使得L成为按关键字自小到大的有效静态链表，L->r[0]为头结点
  */
 void RadixSort(SLList *L)
 {
     int i = ;
     //将L改造成静态链表
     for(i=; i<L->recnum; i++)
         L->r[i].next = i+;
     L->r[L->recnum].next = ;
 #ifdef DEBUG
     printf("将L改造成静态链表\n");
     PrintSList(*L);
 #endif

     ArrType f, e;
     //按最低位优先依次对各关键字进行分配和收集
     for(i=; i<L->keynum; i++){
         //第i趟分配
         Distribute(L->r, i, f, e);
 #ifdef DEBUG
         printf("第%d趟分配---------------------------------------\n");
         PrintSList(*L);
         printf("头指针队列:");
         PrintArr(f, RADIX);
         printf("尾指针队列:");
         PrintArr(e, RADIX);
 #endif
         //第i躺收集
         Collect(L->r, i, f, e);
 #ifdef DEBUG
         printf("第%d趟收集----\n");
         PrintSList(*L);
         printf("按next打印:");
         int p = ;
         for(p=L->r[].next; p; p=L->r[p].next){
             printf("%d%d%d ", L->r[p].keys[], L->r[p].keys[], L->r[p].keys[]);
         }
         printf("\n");
 #endif
     }
 }

 int getRedFromStr(char str[], int i, SLCell *result)
 {
     int key = atoi(str);
     if(key< || key >){
         printf("Error:too big!\n");
         return -;
     }
     int units = , tens = , huns = ;
     //百位
     huns = key/;
     //十位
     tens = (key-*huns)/;
     //个位
     units = (key-*huns-*tens)/;
     result->keys[] = units;
     result->keys[] = tens;
     result->keys[] = huns;
     result->otheritems = 'a'+i-;
     return ;
 }

 int main(int argc, char *argv[])
 {
     SLList L;
     int i = ;
     for(i=; i<argc; i++){
         if(i>MAX_SPACE)
             break;
         if(getRedFromStr(argv[i], i, &L.r[i]) < ){
             printf("Error:only 0-999!\n");
             return -;
         }
     }
     L.keynum = ;
     L.recnum = i-;
     L.r[].next = ;
     L.r[].otheritems = '';
     RadixSort(&L);
     return ;
 }

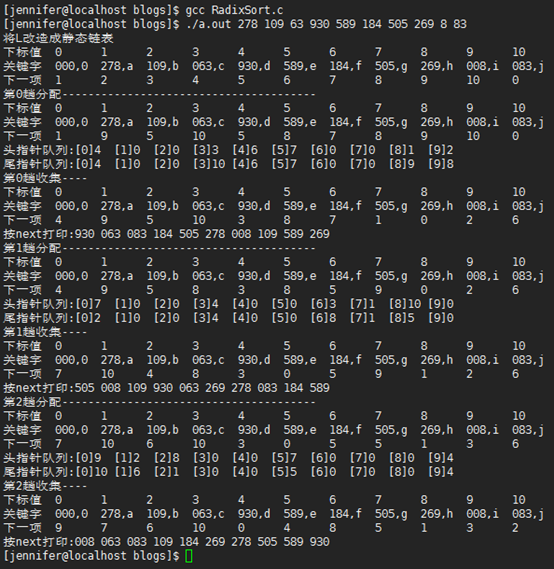
链式基数排序

运行