不学无术的下场——OO第一单元总结

第一单元OO作业总结

第一次作业

​ 第一次作业的要求是对仅有常数和幂函数的式子进行求导。

​ 由于是第一次接触JAVA，对很多东西都还不熟悉，尤其是正则表达式做得不好。当时我的思路如下：

• 建立Poly类，存储若干个幂函数（但是没有把幂函数建立成一个对象，对后面产生了麻烦）
• 先对字符串进行预处理（好坏参半）
• 使用符号作为关键字对原字符串进行分割（好坏参半，原因见后文分析）
• 对特殊符号采用了保护符（有效，但是不够巧妙）
• 进行简单判断之后，把大部分异常交给BigInteger处理（好）
• 在Poly类中，使用Hashmap来进行合并同类项

程序思路分析&更优的思路分析

​ 这一次作业中，我有许多做得不够好的地方。可以说很多问题是不会正则表达式所导致的。

对项的分割：

​ （较优的解决方案）：

​ 写一个通项的正则表达式，（注意第一项和后续项的区别）。然后疯狂match，如果发现有连续匹配到的两项无法连接，或者出现了字符串前后未匹配，则抛出异常。

​

​ （当时我用的比较傻的方案）：

​ 使用+-号作为字符串分割的关键字，调用String自带函数完成分割。但是同时产生了问题，第一个问题是指数中的符号如何处理。我的解决方案是在预处理时，将这样的符号替换成特殊字符A和S，也就是之前说的符号保护。

​ 对于连续的加号减号问题，也是用字符串替换来进行化减。但是直接把形如“+ +”给换成“+”会出现问题，因为“+ +【空格】1“不合法，而”+【空格】1“合法，所以直接替换之后可能出现问题。所以再次需要使用到符号保护问题。

对格式错误的处理

​ 完成了字符串的分割之后，基于实现方法的不同，会有两种不同的情况：

​ （使用正则去判断）：

​ 到这一步基本不会存在非法情况了，因为能匹配进来的字符串都是合法公民（笑）

​ （使用符号分割）：

​ 到这一步之后，我选择的是做一些基础判断，比如是否为常数。是否存在系数以及指数等，如果异常则抛出相应异常。

​ 接着，把字符串再进行分割，分隔成系数，指数部分，然后把得到的结果送给BigInteger处理，其他的格式异常全部由BigInteger构造函数内部进行判断。感觉这样的做法还是挺不错的。只要保证自己分隔方法正确，任何的格式错误均会被BigInteger给捕捉。

项的存储以及求导

​ 为了方便同类项的合并，我采取了Hashmap来进行数据的存取。采用的是<BigInteger,BigInteger>的形式。然后求导的结果是返回一个String，直接输出即可。

​ 但是这样的实现方式并不好。

​ 更优的解决方案：

​ 将项建立为一个单独的类，实现ToString方法，实现求导方法。项的求导返回的还是一个项。多项式求导返回一个新的多项式。多项式实现ToString方法。

​ 这样子，可以在读入数据的时候，调用ToString判断数据是否正确地读入。求导之后得到的结果不会影响多项式本身。再用一次ToString即可观察求导的结果。

被发现的bug&&找bug的思路

​ 我的问题发生在做符号保护这个地方。既然符号保护，就必须要使用一些特殊的字符。而我忘记判断了原始字符串里面有无出现这些特殊字符。所以导致了被人用我的保护字符进行hack的情况。

​ 还有就是对于正则表达式不熟悉，造成[-+]写成了[-|+],然后被hack。。。。

​

找bug的思路：

​ 第一点是对于特殊空白字符的hack。很多同学使用了\\s来进行判断空白字符。于是。。。。正义的\v出场，hack了6个人

​ 第二个点，是出现在多个符号的情况下。形如- - x是合法的，但是有的同学就没判断得出来，认为这个格式错误。hack了2个人

​ 第三个点是，单独一个符号的问题。我的测试数据是“+”，有一个人啥都没输出，有一个人输出了0，共hack2人

​ 第四个点是，当串内为空的时候，是否补0，比如“x-x”。有的同学在这个情况下就输出空串了。。。。hack2人

利用工具对自己代码进行分析

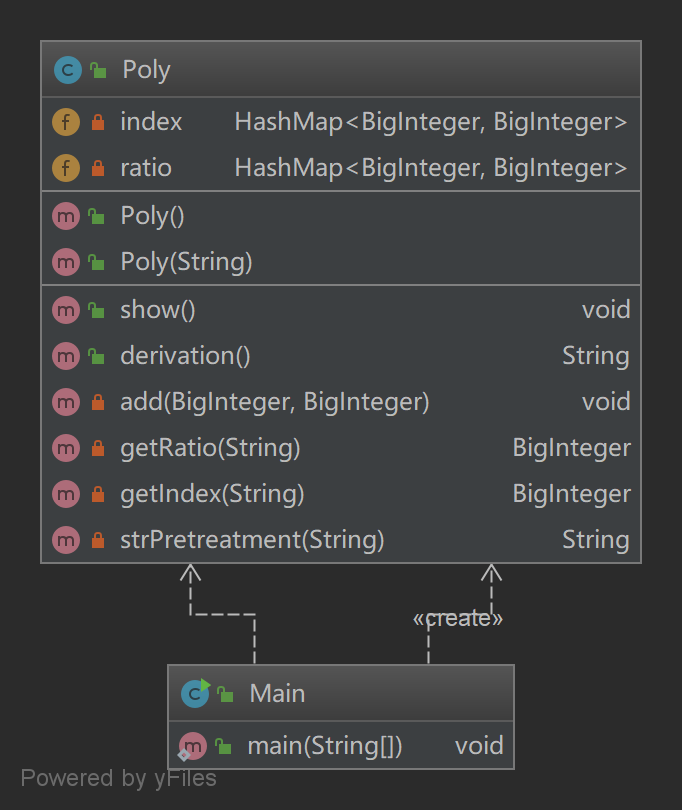
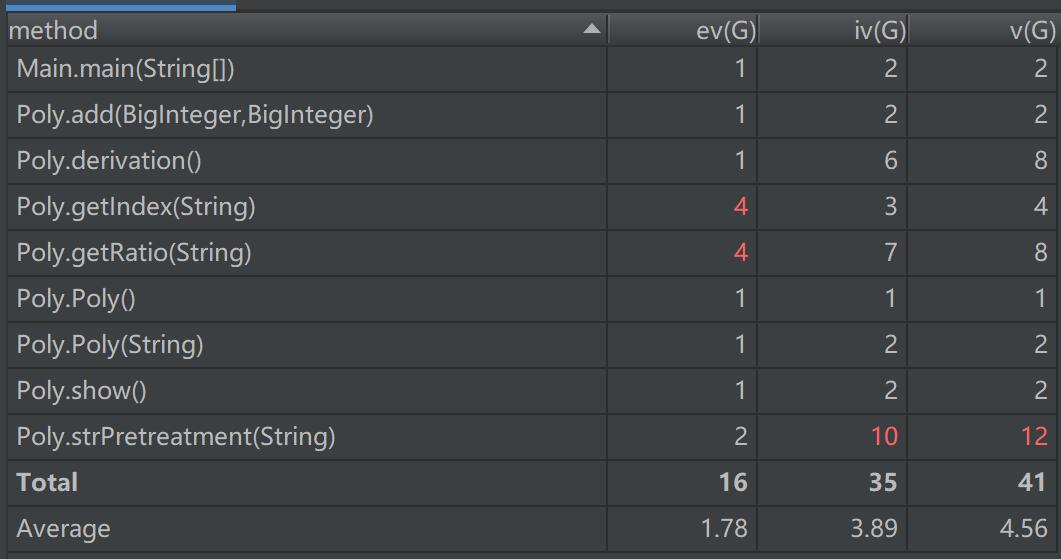
可以看出，主要的问题存在于不会用正则表达式，造成了字符串预处理、获取系数、属于指数这三个部分特别复杂。我的bug也是在这地方产生的。所以，学好正则，减少函数复杂度很有必要。

第二次作业

程序思路分析&更优的思路分析

这一次的作业，要求我们求导的式子变得更加复杂了一点。主要是新增了sin、cos，以及由于乘法所带来的运算符素质三连问题。

对于字符串的分隔

​ 采用双重正则表达式判断：

​ 由于第一次不会正则，吃了大亏。所以这一次作业恶补了一下正则表达式。我采用正则表达式将原字符串分隔成若干个乘法项。然后在构造函数内再对乘法项进行分隔，处理。

​ 这一部分判断格式错误的逻辑是：出现前后未匹配的串，或者是前后匹配项未相连，则扔出格式错误异常

​ 注意理解三连符号出现的原因，还有首项和后续项的区别。

对于程序结构设计

​ （我之前采用的方法：）

• 最上层的是Poly，也就是加法式。使用ArrayList来存储若干个乘法式。

• 每个乘法式内有三个Factor，分别是X，Sin,Cos型，还有一个BigInteger型的系数。（原本想的结构是支持扩展的，但为了优化，这里的代码特化了。）

• 每个Factor里面有一个Type，系数，指数。

求导的时候：

• Factor的求导函数返回Factor的Arraylist,因为型如sin(x)^2^这样的Factor，求导之后的结果会是2*sin(x)*cos(x)

,也就是可能有若干项。所以需要返回的是Arraylist

• Term的求导是基于乘法求导法则的，即一项不求导，乘上其他项全部求导。返回的是一个Term的Arraylist
• Poly的求导是对所有的Term分别求导，然后加入到Arraylist中。
• 对三角函数的优化集成在AddTerm这个函数里面了。

一些感觉还不错的细节：

• 任何级别的求导，返回的均是一个相应的对象，而不是一个String。这样可以方便求导后的化简。
• 在添加Term或者其他东西的时候。我是用了自己写的一个函数，AddTerm。刚开始写的时候，这个函数里面就是一个对Arraylist的添加。但是在后面优化的时候，比如合并，化简。只需要对这个函数修改即可完成。

被发现的bug&&找bug的思路

被发现的bug，其实是我优化的时候犯的糊涂。我在一个函数中试图把sin^2^与cos^2^合并，但是随后紧接着又试图通过拆分另一项来与当前项进行合并。于是出现了优化--复原--优化--复原的无穷递归。

找bug的时候，我们那一组的成员都比较的坚不可摧。我是采用写一个比较复杂的式子，然后随机加入空格，或者符号来进行修改。

然后在本地，先将下载下来的代码编译。分别放入文件夹中，再编写cmd脚本来进行本地的测试。

然后就基本上是加特林突突突的过程，本地运行发现有某个代码比较异常，那么就揪出来看看。

利用工具对自己的代码进行分析

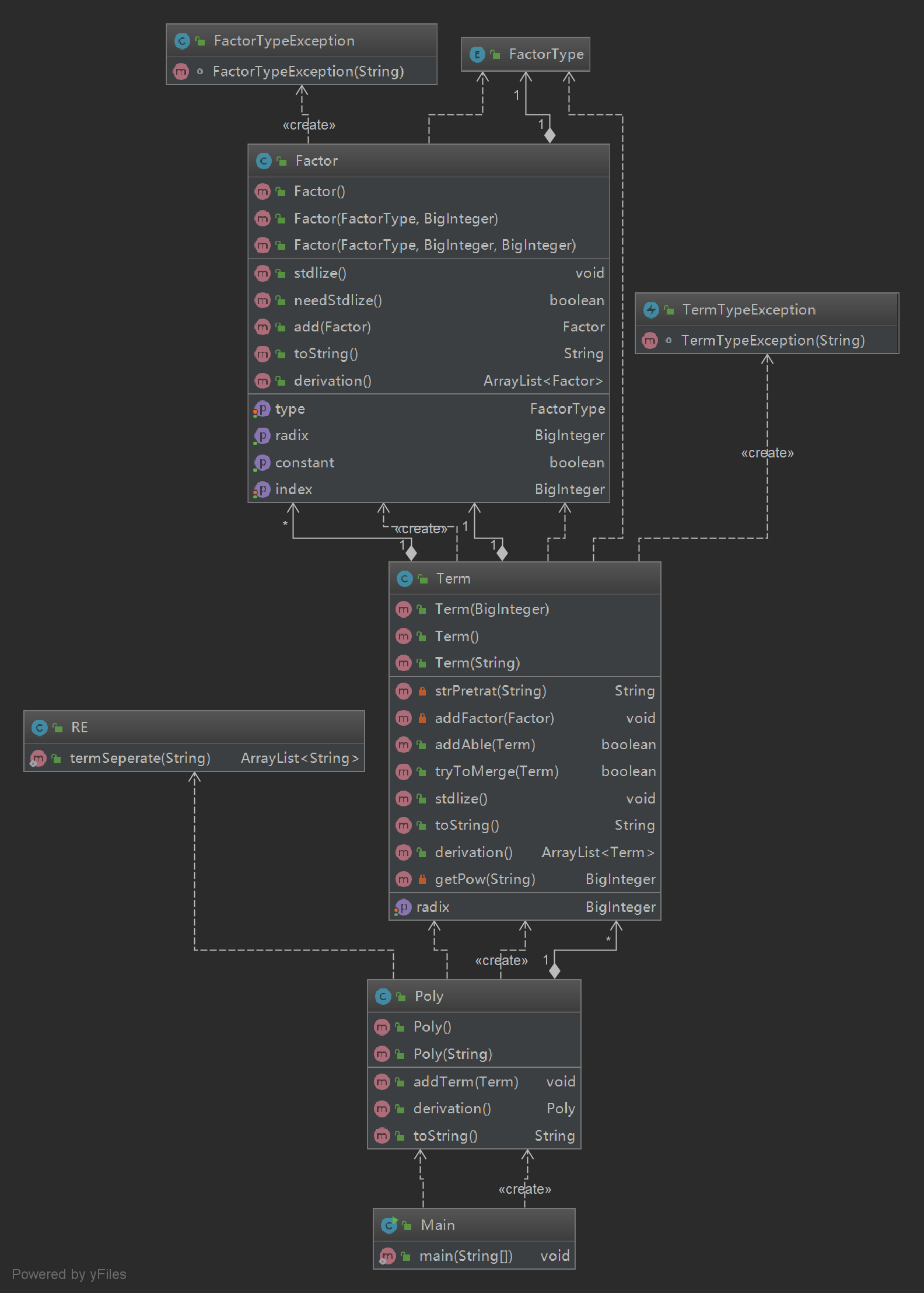
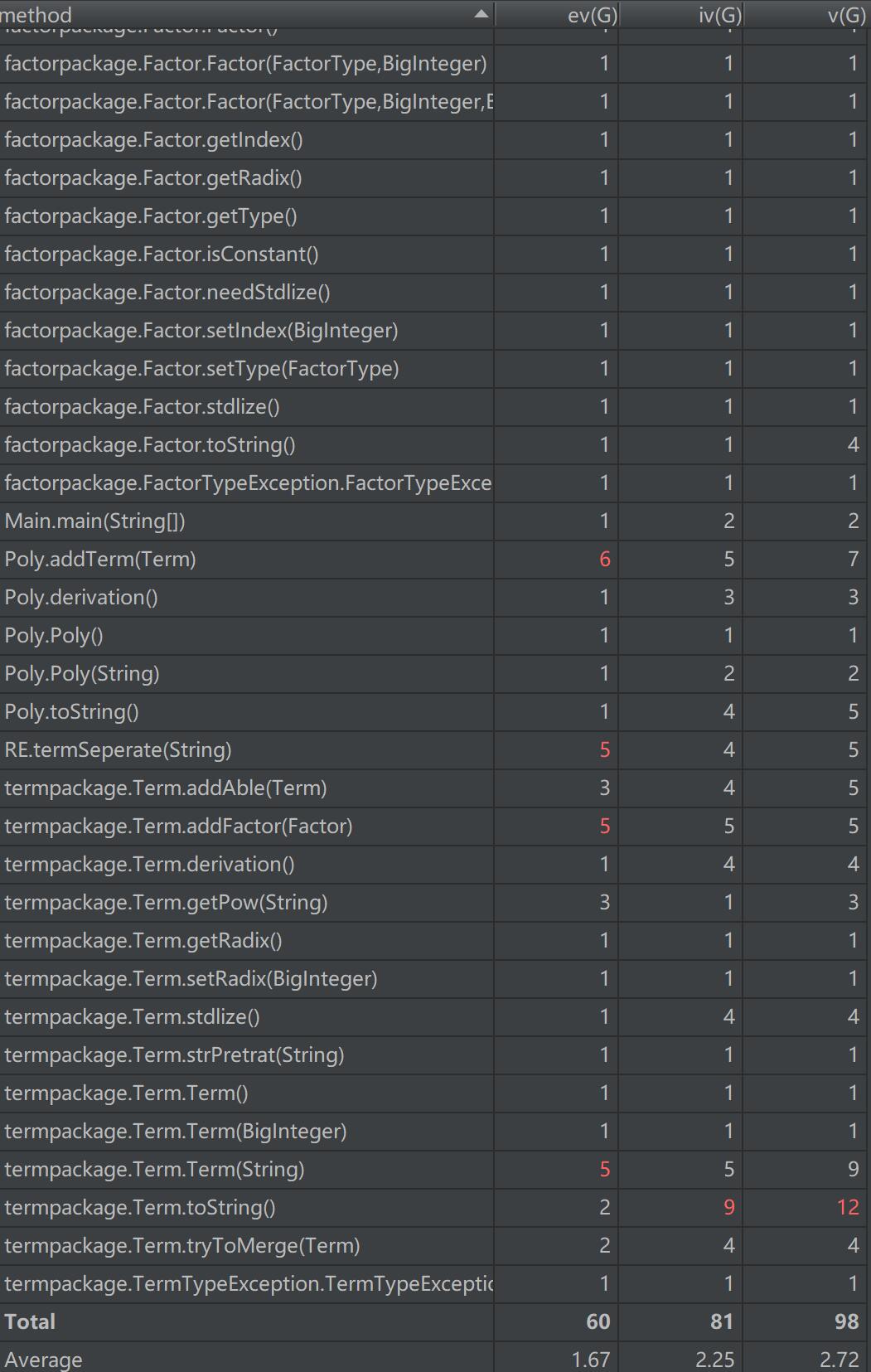
可以看出，复杂度比较高的几个点存在于对于表达式化简的部分。也就是说，其他部分都相对来说比较简单。说明我的架构还是可以接受的。

第三次作业

这一次，比较麻烦。因为出现了嵌套

最初构想的思考过程&&架构&&数据处理

架构部分

​ 对于加法项和乘法项，其实改造的时候都好说。因为都是Arraylist，往后添加就好了。问题就出现在sin，cos复合的情况。求导过程中肯定要出现链式法则，而链式法则大概是f(g(x))这样的形式，所以也就是说，一个表达式要嵌套一个表达式。

​ 既然出现了嵌套相同类型，就想到了递归算法。而什么时候停止递归下去呢？遇到基本项，比如x，sin(x)，cos(x)这样的情况就停止。

​ 然后我就联想到了，可以把整个表达式建成一棵子节点不定的表达式树。他的节点有这几种类型：

• 叶节点：
  • sin(x)
  • cos(x)
  • x
  • 常数
• 只有一个儿子的节点
  • sin(f(x))型
  • cos(f(x))型
• 有多个儿子的节点
  • 加法类型
  • 乘法类型

数据处理部分

​ 在正则表达式中，有一种东西叫做平衡组。使用平衡组能解决对于成对括号的匹配问题，从而把sin(f(x))之类的项给提出，以交给下一级处理。

实际遇到的问题

架构方面

前文给出的架构，实际上就是一个面向对象中的继承关系。我希望达到的目标是，向程序投喂一个String，然后程序自动判断对应的类型，建立相应类型的对象。但以我的知识无法解决（据说这个是要用工厂方法。这个我之后去学学看。。。。）

于是只能把所有类都归纳成一个Term，然后在其中定义一个Type属性，根据这个属性来判断这个对象的行为。

这也就造成了写出来的代码特别丑。

当然，也有因为时间的原因啦。我只有一天的时间去写完这作业，不敢轻举妄动。

数据处理部分

JAVA的正则表达式不支持平衡组！！！！！

既然正则不好使了，原本想过利用状态机加上递归的方法去判断并分割式子的（好像这叫做递归下降？），但是助教说不建议用状态机。并且之前自己没写过这样的东西，所以就不敢乱来。

我实际使用的是小正则判断加上for循环平衡搜索

• 先用正则表达式判断是否为x，sin，cos（这一步我最后出了bug）
• 如果不是，则试图采用加减法分割原表达式，分隔的时候，需要保证分隔的点之前括号是匹配的，以保证不会分割掉括号内的内容
• 再试图按照乘法类型分割原表达式，同样要求括号匹配。
• 如果上述尝试都无法成功，抛出无法识别类型异常

之所以我先分割加减法再分割乘除法，是因为乘法优先级更高。

被发现的bug&&找bug的思路

我的bug有两点：

• 忘了还有一种类型是+（f（x）），少判断一种类型，直接爆炸
• 如果出现了*++5这种情况。我的分割函数没有识别出来这个是一个格式错误

于是炸得香。强测加互测共炸了20个点。结果打了两次补丁就修完了。。。。

找bug的思路：

​ 多层括号嵌套加上乘法

​ 如果没有对括号嵌套进行优化，如剥去外层的括号。那么多层括号很可能就直接让程序tle了。特别是加上乘法之后，深层树进行乘法运算，那酸爽。。。

​ 一发入魂，hack了6个人

​ 格式分隔错误

​ 这一次无法使用正则表达式了，所以也就是说，在分割字符串的时候肯定会有很多容易错的地方。

​ 我写了一个比较复杂的式子，然后在里面把能加符号的地方全部加上符号，再配合以空格。hack了2人

利用工具对自己的代码进行分析

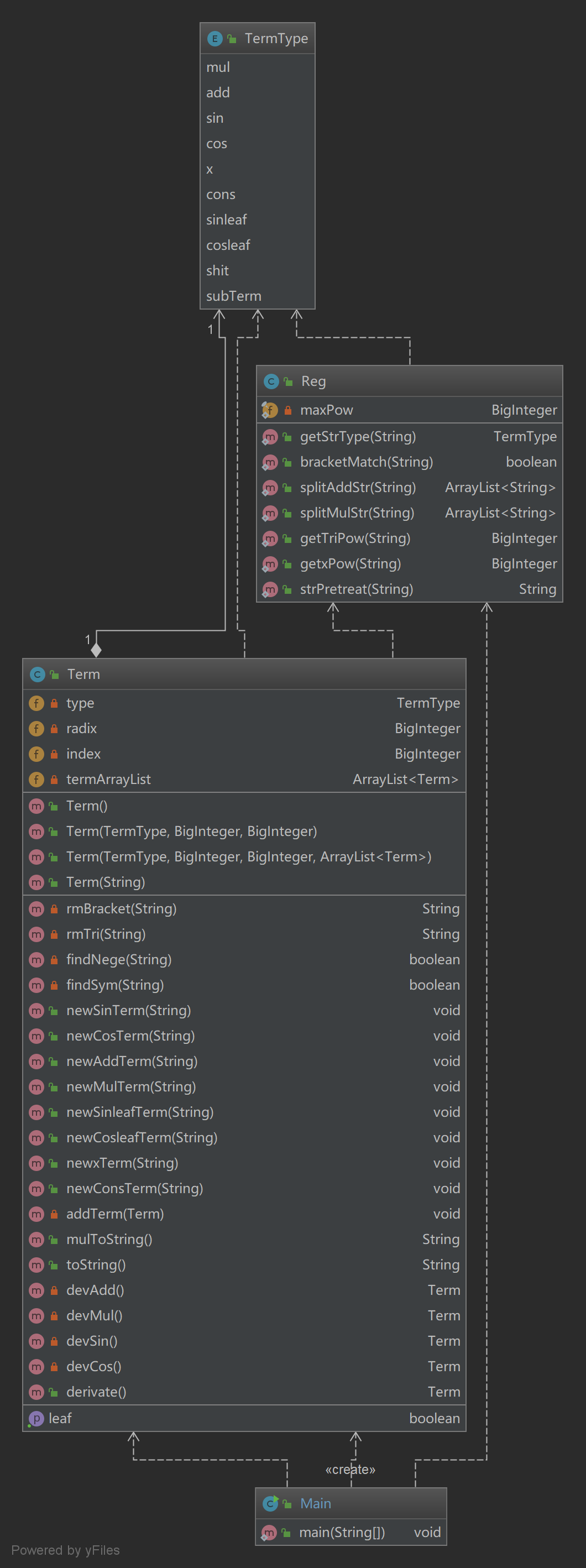
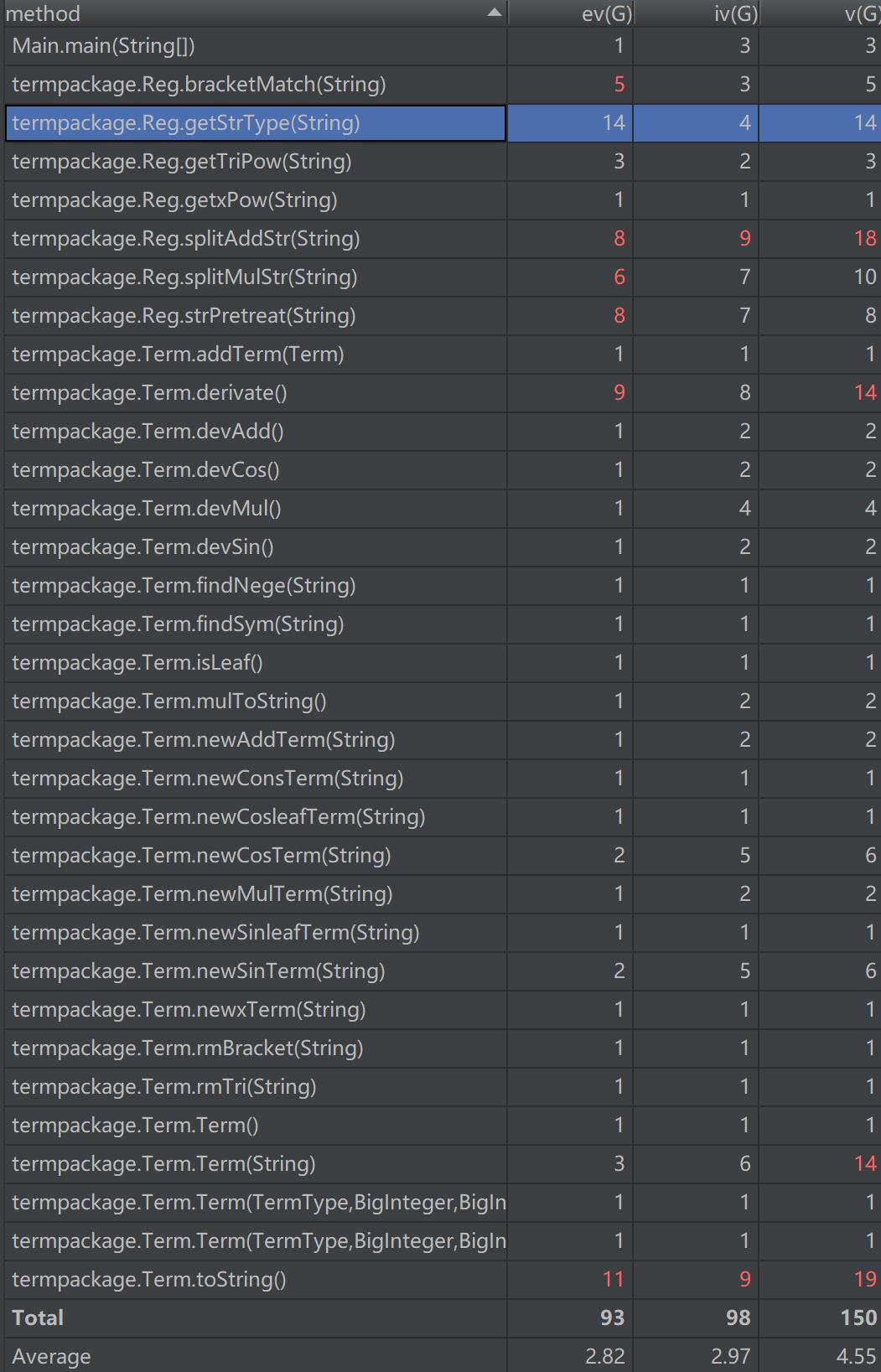
可以看出，这一次的代码是写得真的丑。主要是我的知识无法支撑我的架构，于是只能以比较粗暴的方式去写了。所以JAVA基础知识还是要学好，以我为诫。。。