HDU 2475 BOX 动态树 Link-Cut Tree

Box

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

【Problem Description】

There are N boxes on the ground, which are labeled by numbers from 1 to N. The boxes are magical, the size of each one can be enlarged or reduced arbitrarily. Jack can perform the “MOVE x y” operation to the boxes: take out box x; if y = 0, put it on the ground; Otherwise, put it inside box y. All the boxes inside box x remain the same. It is possible that an operation is illegal, that is, if box y is contained (directly or indirectly) by box x, or if y is equal to x. In the following picture, box 2 and 4 are directly inside box 6, box 3 is directly inside box 4, box 5 is directly inside box 1, box 1 and 6 are on the ground.

The picture below shows the state after Jack performs “MOVE 4 1”:

Then he performs “MOVE 3 0”, the state becomes:

During a sequence of MOVE operations, Jack wants to know the root box of a specified box. The root box of box x is defined as the most outside box which contains box x. In the last picture, the root box of box 5 is box 1, and box 3’s root box is itself.

 

【Input】

Input contains several test cases. For each test case, the first line has an integer N (1 <= N <= 50000), representing the number of boxes. Next line has N integers: a1, a2, a3, ... , aN (0 <= ai <= N), describing the initial state of the boxes. If ai is 0, box i is on the ground, it is not contained by any box; Otherwise, box i is directly inside box ai. It is guaranteed that the input state is always correct (No loop exists). Next line has an integer M (1 <= M <= 100000), representing the number of MOVE operations and queries. On the next M lines, each line contains a MOVE operation or a query:

1.  MOVE x y, 1 <= x <= N, 0 <= y <= N, which is described above. If an operation is illegal, just ignore it.

2.  QUERY x, 1 <= x <= N, output the root box of box x.

 

【Output】

For each query, output the result on a single line. Use a blank line to separate each test case.

 

【Sample Input】

QUERY
QUERY
MOVE
MOVE
QUERY 

MOVE
QUERY
MOVE
QUERY 

【Sample Output】

【题意】

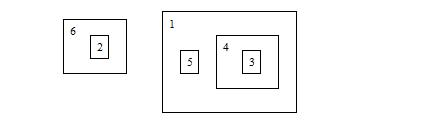
动态地维护一些盒子套盒子的操作，询问根。

【分析】

盒子与盒子的关系可以直观地用树的结构来表示，一个结点下的子结点可以表示大盒子里面直接套着的小盒子。

所以本题就是一个裸的Link-Cut Tree模型了。

关于LCT树，还是推荐Yang Zhe的QTREE论文吧。

动态树是用访问操作来划分树链，对于每一条树链，使用Splay来维护，用深度作为splay的左右关系。

看了很多代码，觉得还是写不好，总觉得别人的用起来不顺，最后是在自己原来Splay的基础上改的。

原本的整棵树是个splay，但是在LCT中，整棵树是由很多棵分散的Splay组合起来的，于是在其中的一些点上加上root标记，表示以这一点为根下面可以形成一棵splay树。多个这样的splay组合完成之后就是一棵LCT了。

后面的代码中加入了输入输出挂。。。。。。

 /* ***********************************************
 MYID    : Chen Fan
 LANG    : G++
 PROG    : HDU 2475
 ************************************************ */

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>

 using namespace std;

 #define MAXN 50010

 int sons[MAXN][];
 int father[MAXN],pathfather[MAXN],data[MAXN];
 bool root[MAXN];
 int spttail=;

 void rotate(int x,int w) //rotate(node,0/1)
 {
     int y=father[x];

     sons[y][!w]=sons[x][w];
     if (sons[x][w]) father[sons[x][w]]=y;
     father[x]=father[y];
     if (father[y]&&(!root[y])) sons[father[y]][y==sons[father[y]][]]=x;
     sons[x][w]=y;
     father[y]=x;

     if (root[y])
     {
         root[x]=true;
         root[y]=false;
     }
 }

 void splay(int x) //splay(node)
 {
     while(!root[x])
     {
         if (root[father[x]]) rotate(x,x==sons[father[x]][]);
         else
         {
             int t=father[x];
             int w=(sons[father[t]][]==t);
             if (sons[t][w]==x)
             {
                 rotate(x,!w);
                 rotate(x,w);
             } else
             {
                 rotate(t,w);
                 rotate(x,w);
             }
         }
     }
 }

 void access(int v)
 {
     int u=v;
     v=;
     while(u)
     {
         splay(u);
         root[sons[u][]]=true;
         sons[u][]=v;
         root[v]=false;
         v=u;
         u=father[u];
     }
 }

 int findroot(int v)
 {
     access(v);
     splay(v);
     while (sons[v][]) v=sons[v][];
     //splay(v,0);
     return v;
 }

 void cut(int v)
 {
     access(v);
     splay(v);
     father[sons[v][]]=;
     root[sons[v][]]=true;
     sons[v][]=;
 }

 void join(int v,int w)
 {
     if (!w) cut(v);
     else
     {
         access(w);
         splay(w);
         int temp=v;
         while(!root[temp]) temp=father[temp];
         if (temp!=w)
         {
             cut(v);
             father[v]=w;
         }
     }
 }

 int INT()
 {
     char ch;
     int res;
     while (ch=getchar(),!isdigit(ch));
     for (res = ch - '';ch = getchar(),isdigit(ch);)
         res = res *  + ch - '';
     return res;
 }

 char CHAR()
 {
     char ch, res;
     while (res = getchar(), !isalpha(res));
     while (ch = getchar(), isalpha(ch));
     return res;
 }

 int main()
 {
     //freopen("2475.txt","r",stdin);

     int n;
     double flag=false;
     while(scanf("%d",&n)!=EOF)
     {
         if (flag) printf("\n");
         flag=true;

         memset(father,,sizeof(father));
         memset(sons,,sizeof(sons));
         for (int i=;i<=n;i++)
         {
             //scanf("%d",&father[i]);
             father[i]=INT();
             root[i]=true;
         }

         int m;
         m=INT();
         for (int i=;i<=m;i++)
         {
             char s=CHAR();
             if (s=='M')
             {
                 int x,y;
                 x=INT();
                 y=INT();
                 join(x,y);
             } else
             {
                 int q;
                 q=INT();
                 printf("%d\n",findroot(q));
             }
         }
     }

     return ;
 }