NOI十连测 第三测 T1

这么二逼的题考试的时候我想了好久，我真是太弱了。。。

首先，由于ans都乘上了i*(i-1)/2，实际上要求的就是每个数的所有可能出现次数*这个数的权值。

我们发现，每个数的本质是一样的，我们记一个sum为数的总和，这样只要统计一次就OK了。

我们把每次的选择抽象成有向边，每个状态视为点，这样就构成一个有根树。

如图

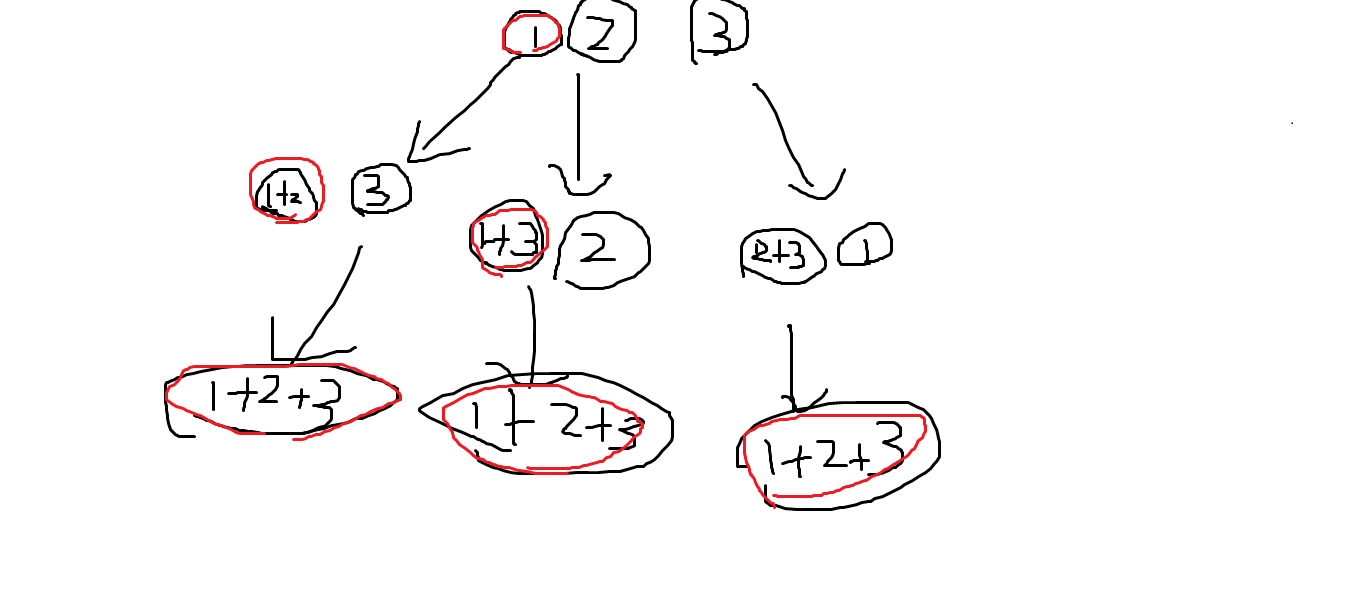
我们只考虑1对答案的贡献。如图，在每层计算当前合并对答案的贡献，也就是要能得知我在这个节点选择合并1或者1的联通块，那么我能覆盖到几个叶子节点？

那么就变成O(n)的组合数学题了。。对了，组合数用到的阶乘和阶乘逆元可以O(n)预处理。

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #define ll long long
 int ans=,a[],n,cnt[],size[];
 const ll Mod=;
 ll sum,jcny[],jc[],f[],son[],Num[];
 int read(){
     int t=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-') f=-;ch=getchar();}
     while (''<=ch&&ch<=''){t=t*+ch-'';ch=getchar();}
     return t*f;
 }
 bool cmp(const int &a,const int &b){
     return a>b;
 }
 ll gcd(ll a,ll b){
     if (b==) return a;
     else return gcd(b,a%b);
 }
 void exgcd(ll a,ll b,ll &x,ll &y){
     if (b==){
         x=;y=;
         return;
     }
     exgcd(b,a%b,x,y);
     ll t=x;
     x=y;
     y=t-(a/b)*y;
 }
 void init(){
     jc[]=;jcny[]=;
     for (ll i=;i<=n+;i++) jc[i]=(jc[i-]*i)%Mod;
     ll x,y;
     exgcd(jc[n+],Mod,x,y);
     jcny[n+]=(x%Mod+Mod)%Mod;
     for (int i=n;i>=;i--) jcny[i]=(jcny[i+]*(i+))%Mod;
 }
 ll C(int n,int m){
     return (((jc[n]*jcny[m])%Mod)*jcny[n-m])%Mod;
 }
 int dfs(int x1,int x2,int x3,int x4,int x5,int num,int res){
     int b[];
     int Res=;
     if (num==){
         ans=(ans+res)%Mod;
         return Res;
     }
     b[]=x1;b[]=x2;b[]=x3;b[]=x4;b[]=x5;
     std::sort(b,b+num,cmp);
     for (int i=;i<num;i++)
      for (int j=i+;j<num;j++){
             b[i]+=b[j];int tmp=b[j];b[j]=;std::swap(b[j],b[num-]);
             Res+=dfs(b[],b[],b[],b[],b[],num-,(res+b[i])%Mod);
             std::swap(b[j],b[num-]);
             b[i]-=tmp;b[j]=tmp;
     }
     return Res;
 }
 ll inv(ll a){
     ll x,y;
     exgcd(a,Mod,x,y);
     return x;
 }
 void sbpianfen(){
     int k=dfs(a[],a[],a[],a[],a[],n,);
     printf("%d\n",ans);
 }
 ll A(int n,int m){
     return (jc[n]*jcny[n-m])%Mod;
 }
 ll Pow(ll x,ll y){
     ll res=;
     while (y){
         if (y%) res=(res*x)%Mod;
         x=(x*x)%Mod;
         y/=;
     }
     return res;
 }
 void sxpianfen(){
     ll res=;
     son[]=;son[]=;
     for (int i=,num=n;i<=n;i++,num--)
      son[i]=(son[i-]*C(num,))%Mod;//这行
     Num[n-]=;Num[n]=;Num[n+]=;Num[n+]=;
     for (int i=n-,num=;i>=;i--,num++)
       Num[i]=(Num[i+]*C(num+,))%Mod;  //叶子
     for (int i=,num=n;i<=n-;i++,num--){
         res=(res+(son[i]*Num[i+])%Mod*(num-))%Mod;
     }
     res=(res*sum)%Mod;
     printf("%lld\n",res);
 }
 int main(){
     n=read();init();
     for (int i=;i<=n;i++)
      a[i]=read(),sum=(sum+a[i])%Mod;
     if (n<=){sbpianfen();return ;}
     if (n<=){sxpianfen();return ;}
 }