GCD - Extreme (II) （欧拉函数妙用）

https://cn.vjudge.net/problem/UVA-11426

题意：求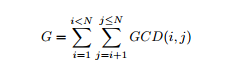

解题思路：我们可以定义一个变量dis【n】，dis【n】意为1~（n-1）与n的gcd（最大公约数）的总和，那么可以得到ans【n】=ans【n-1】+dis【n】，那么问题来了，如何求dis【n】呢？我们可以假设一个变量a【i】，a【i】为gcd（n，m）==i   （1<=m<n）的个数，那么dis【n】=sum{a【i】*i}了，由gcd（n，m）=i得，gcd（n/i，m/i）=1，即dis【n】=sum{phi【n/i】*i}。

#include<iostream>
#include<cstdio>
#include<string>
#include<algorithm>
using namespace std;
#define inf 0x3f3f3f3f
#define ri register int
typedef long long ll;

inline ll gcd(ll i,ll j){
	return j==0?i:gcd(j,i%j);
}
inline ll lcm(ll i,ll j){
	return i/gcd(i,j)*j;
}
inline void output(int x){
	if(x==0){putchar(48);return;}
	int len=0,dg[20];
	while(x>0){dg[++len]=x%10;x/=10;}
	for(int i=len;i>=1;i--)putchar(dg[i]+48);
}
inline void read(int &x){
    char ch=x=0;
    int f=1;
    while(!isdigit(ch)){
    	ch=getchar();
		if(ch=='-'){
			f=-1;
		}
	}
    while(isdigit(ch))
        x=x*10+ch-'0',ch=getchar();
        x=x*f;
}
const int maxn=4e6+5;
ll ans[maxn];
ll dis[maxn];
int phi[maxn];
int vis[maxn];
void work(){
	for(int i=1;i<=4e6+1;i++){
		phi[i]=i;
	}
	for(int i=2;i<=4e6+1;i++){
		if(vis[i]==0){
			for(int j=i;j<=4e6+1;j+=i){
				vis[j]=1;
				phi[j]=phi[j]/i*(i-1);
			}
		}
	}
	for(int i=1;i<=4e6+1;i++){
		for(int j=i*2;j<=4e6+1;j+=i){
			dis[j]+=phi[j/i]*i;
		}
	}
	ans[2]=dis[2];
	for(int i=3;i<=4e6+1;i++){
		ans[i]=ans[i-1]+dis[i];
	}
	int n;
	while(scanf("%d",&n)&&n>0){
		printf("%lld\n",ans[n]);
	}
	return ;
}
int main(){
	work();
	return 0;
}