qbxt的题：找一个三元环

有向图中找一个三元环

题意：

考虑 N 个人玩一个游戏， 任意两个人之间进行一场游戏 （共 N*(N-1)/2 场），且每场一定能分出胜负。现在，你需要在其中找到三个人构成的这样的局面：A战胜B，B战胜C，C战胜A。

分析：

注意到一个重要的条件，就是图中有n*(n-1)/2条有向边。

正解的做法：在图中找一个环，如果存在一个环，那么一定存在一个三元环。

为什么？

对于一个环，是这样的，枚举除起点外的前两个点，即123，如果3可以到1，那么说明存在一个三元环。

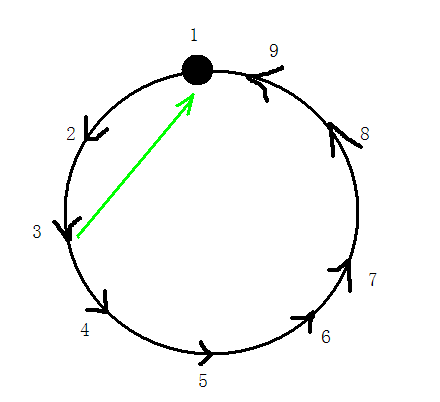
否则，说明1一定连向了3，然后判断第4是否连向1即可。依次类推。

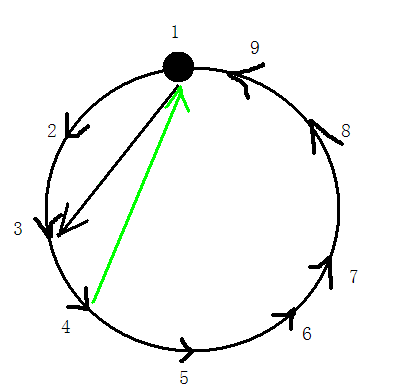
一直判断下去，到8号点，可行的就行了。

否则，剩下的三个点一定可以了。

代码：

 #include<cstdio>
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cctype>
 #include<cmath>
 #include<set>
 #include<queue>
 #include<vector>
 #include<map>
 using namespace std;
 typedef long long LL;

 inline int read() {
     int x = , f = ; char ch = getchar(); for (; !isdigit(ch); ch=getchar()) if (ch=='-') f=-;
     for (; isdigit(ch); ch=getchar()) x = x *  + ch - ''; return x * f;
 }

 const int N = ; 

 char s[N][N];
 int top, n, vis[N], sk[N], pos[N];
 vector<int> ans;

 void pr() {
     for (int i = ; i < ans.size() - ; ++i) {
         if (s[ans[i + ]][ans[]] == '') {
             cout << ans[] << " " << ans[i] << " " << ans[i + ];
             exit();
         }
     }
 }

 void dfs(int u) {
     vis[u] = , sk[++top] = u; pos[u] = top;
     for (int i = ; i <= n; ++i) {
         if (s[u][i] != '') continue;
         if (vis[i] == ) {
             int len = top - pos[i] + ;
             for (int j = pos[i]; j <= top; ++j) ans.push_back(sk[j]);
             pr();
         } else if (vis[i] == ) {
             dfs(i);
         }
     }
     --top; vis[u] = ;
 }

 int main() {

     freopen("game.in","r",stdin);
     freopen("game.out","w",stdout);

     n = read();
     for (int i = ; i <= n; ++i) scanf("%s",s[i] + );
     for (int i = ; i <= n; ++i) {
         if (!vis[i]) dfs(i);
     }
     puts("-1");
     return ;
 }
 /*
 5
 00100
 10000
 01001
 11101
 11000 

 */