BZOJ4652 NOI2016循环之美（莫比乌斯反演+杜教筛）

　　因为要求数值不同，不妨设gcd(x,y)=1。由提示可以知道，x/y是纯循环小数的充要条件是x·k^len=x(mod y)。因为x和y互质，两边同除x，得k^len=1(mod y)。那么当且仅当k和y互质，存在len使该式成立。

　　于是现在要求的就是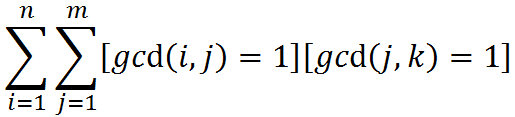

　　k是固定的，先不管后面一部分。套路地化式子：

　　

　　

　　

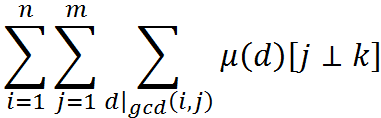
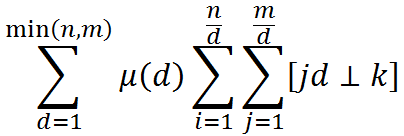
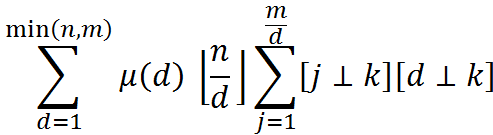
　　设f(i)=[i⊥k]。注意到k很小，并且显然有gcd(j,k)=gcd(j%k,k)。于是O(k)的预处理出f的前缀和。

　　

　　那么几乎已经做到线性了，能拿到84分，感觉非常棒。

　　然而要A掉还需要低于线性的做法。看到两个下取整就会特别想整除分块。那么现在我们需要求的是g(i)=μ(i)*[i⊥k]的前缀和。

　　继续套路地化：

　　

　　

　　

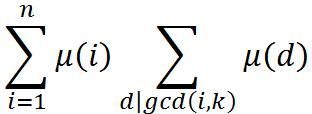
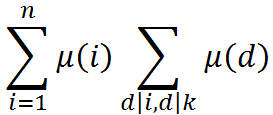
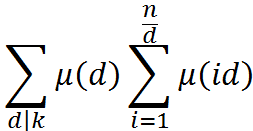
　　注意到若i和d不互质，则μ(id)=0，否则μ(i)·μ(d)=μ(id)。

　　

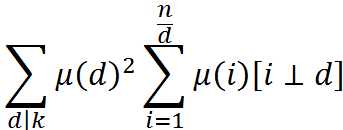
　　可以发现后面一个求和和我们的g函数形式上是一样的。于是可以递归求解，记忆化一下。边界k=1时用杜教筛求出μ的前缀和。

　　考虑复杂度。上面式子中的n有√N种（⌊N/d⌋的取值个数），k有√K种（K的因子个数）。转移时枚举因子√K种。把μ筛到2e7的话，杜教筛的次数非常少。于是总复杂度约为O(k√n+n^2/3)，且远远跑不满。

　　以上复杂度分析均为口胡。总之O(能过)。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
#define N 20000010
#define K 2010
int n,m,k,mobius[N],prime[N],sum[K],cnt=;
long long ans=;
bool flag[N];
map<int,int> miu;
map<int,int> G[K];
int gcd(int n,int m){return m==?n:gcd(m,n%m);}
inline int f(int n){return sum[k]*(n/k)+sum[n%k];}
int calc(int k)
{
    if (k<=min(min(n,m),N-)) return mobius[k];
    if (miu[k]) return miu[k];
    int s=;
    for (int i=;i<=k;i++)
    {
        int t=k/(k/i);
        s-=(t-i+)*calc(k/i);
        i=t;
    }
    miu[k]=s;
    return s;
}
int g(int n,int k)
{
    if (n==) return ;
    if (G[k][n]) return G[k][n];
    if (k==) return calc(n);
    int s=;
    for (int i=;i*i<=k;i++)
    if (k%i==)
    {
        if (mobius[i]-mobius[i-]) s+=g(n/i,i);
        if (i*i!=k&&(mobius[k/i]-mobius[k/i-])) s+=g(n/(k/i),k/i);
    }
    G[k][n]=s;
    return s;
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj4652.in","r",stdin);
    freopen("bzoj4652.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    n=read(),m=read(),k=read();
    flag[]=;mobius[]=;
    for (int i=;i<=max(min(min(n,m),N-),k);i++)
    {
        if (!flag[i]) prime[++cnt]=i,mobius[i]=-;
        for (int j=;j<=cnt&&prime[j]*i<=min(min(n,m),N-);j++)
        {
            flag[prime[j]*i]=;
            if (i%prime[j]==) break;
            else mobius[prime[j]*i]=-mobius[i];
        }
    }
    for (int i=;i<=max(min(min(n,m),N-),k);i++) mobius[i]+=mobius[i-];
    for (int i=;i<=k;i++)
    sum[i]=sum[i-]+(gcd(i,k)==);
    for (int i=;i<=min(n,m);i++)
    {
        int t=min(n/(n/i),m/(m/i));
        ans+=1ll*(n/i)*f(m/i)*(g(t,k)-g(i-,k));
        i=t;
    }
    cout<<ans;
    return ;
}