四元数与欧拉角（RPY角）的相互转换

• RPY角与Z-Y-X欧拉角

　　描述坐标系{B}相对于参考坐标系{A}的姿态有两种方式。第一种是绕固定（参考）坐标轴旋转：假设开始两个坐标系重合，先将{B}绕{A}的X轴旋转$\gamma$，然后绕{A}的Y轴旋转$\beta$，最后绕{A}的Z轴旋转$\alpha$，就能旋转到当前姿态。可以称其为X-Y-Z fixed angles或RPY角(Roll, Pitch, Yaw)。

　　Roll:横滚

　　Pitch: 俯仰

Yaw: 偏航（航向）

　　由于是绕固定坐标系旋转，则旋转矩阵为（$c\alpha$ is shorthand for $\cos\alpha$, $s\alpha$ is shorthand for $\sin\alpha$,and so on.）

$$R_{XYZ}(\gamma,\beta,\alpha)=R_Z(\alpha)R_Y(\beta)R_X(\gamma)=\begin{bmatrix}
c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\
s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\
-s\beta& c\beta s\gamma & c\beta c\gamma
\end{bmatrix}$$

　　另一种姿态描述方式是绕自身坐标轴旋转：假设开始两个坐标系重合，先将{B}绕自身的Z轴旋转$\alpha$，然后绕Y轴旋转$\beta$，最后绕X轴旋转$\gamma$，就能旋转到当前姿态。称其为Z-Y-X欧拉角，由于是绕自身坐标轴进行旋转，则旋转矩阵为：

$$R_{Z'Y'X'}(\alpha,\beta,\gamma)=R_Z(\alpha)R_Y(\beta)R_X(\gamma)=\begin{bmatrix}
c\alpha c\beta & c\alpha s\beta s\gamma-s\alpha c\gamma & c\alpha s\beta c\gamma+s\alpha s\gamma\\
s\alpha c\beta & s\alpha s\beta s\gamma+c\alpha c\gamma & s\alpha s\beta c\gamma-c\alpha s\gamma\\
-s\beta& c\beta s\gamma & c\beta c\gamma
\end{bmatrix}$$

　　可以发现这两种描述方式得到的旋转矩阵是一样的，即绕固定坐标轴X-Y-Z旋转$(\gamma,\beta,\alpha)$和绕自身坐标轴Z-Y-X旋转$(\alpha,\beta,\gamma)$的最终结果一样，只是描述的方法有差别而已。In gerenal: three rotations taken about fixed axes yield the same final orientation as the same three rotations taken in opposite order about the axes of the moving frame.

• Axis-Angle与四元数

　　绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设等效旋转轴方向向量为$\vec{K}=[k_x,k_y,k_z]^T$，等效旋转角为$\theta$，则四元数$q=(x,y,z,w)$，其中：

$$\begin{align*}
x &= k_x \cdot sin \frac{\theta}{2}\\
y &= k_y \cdot sin \frac{\theta}{2}\\
z &= k_z \cdot sin \frac{\theta}{2}\\
w &= cos \frac{\theta}{2}
\end{align*}$$

　　且有$x^2+y^2+z^2+w^2=1$

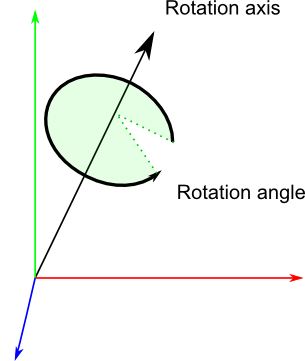
　　即四元数存储了旋转轴和旋转角的信息，它能方便的描述刚体绕任意轴的旋转。

　　四元数转换为旋转矩阵：

$$R=\begin{bmatrix}
1-2y^2-2z^2 & 2(xy-zw) & 2(xz+yw)\\
2(xy+zw) & 1-2x^2-2z^2 & 2(yz-xw)\\
2(xz-yw)& 2(yz+xw) & 1-2x^2-2y^2
\end{bmatrix}$$

　　已知旋转矩阵为：

　　则对应的四元数为：

---

• 四元数与欧拉角的相互转换

　　定义两个四元数：

　　

　　

　　其中 表示矢量

 

；而

 

表示矢量

 

四元数加法：

　　跟复数、向量和矩阵一样，两个四元数之和需要将不同的元素加起来。

　　加法遵循实数和复数的所有交换律和结合律。

四元数乘法：

　　四元数的乘法的意义类似于矩阵的乘法，可以表示旋转的合成。当有多次旋转操作时，使用四元数可以获得更高的计算效率。

　　由于四元数乘法的非可换性，pq并不等于qp，qp乘积的向量部分是：

　　

　　Mathematica中有四元数相关的程序包Quaternions Package，需要先导入才能使用。下面计算了三个四元数的乘积：

<<Quaternions`     （* This loads the package *）
Quaternion[2, 1, 1, 3] ** Quaternion[2, 1, 1, 0] ** Quaternion[1, 1, 1, 1]    (* Be sure to use ** rather than * when multiplying quaternions *)

　　计算结果为：Quaternion[-12, 4, 14, 2]

 

　　那么将Z-Y-X欧拉角（或RPY角：绕固定坐标系的X-Y-Z依次旋转$\alpha$,$\beta$,$\gamma$角）转换为四元数：

$$q=\begin{bmatrix}\cos\frac{\gamma}{2}\\ 0\\ 0\\ \sin\frac{\gamma}{2}\end{bmatrix} \begin{bmatrix}\cos\frac{\beta}{2}\\ 0\\ \sin\frac{\beta}{2}\\ 0\end{bmatrix} \begin{bmatrix}\cos\frac{\alpha}{2}\\ \sin \frac{\alpha}{2}\\ 0\\ 0\end{bmatrix}=\begin{bmatrix}
\cos\frac{\alpha}{2}\cos\frac{\beta}{2}\cos\frac{\gamma}{2}+\sin\frac{\alpha}{2}\sin\frac{\beta}{2}\sin\frac{\gamma}{2}\\
\sin\frac{\alpha}{2}\cos\frac{\beta}{2}\cos\frac{\gamma}{2}-\cos\frac{\alpha}{2}\sin\frac{\beta}{2}\sin\frac{\gamma}{2}\\ \cos\frac{\alpha}{2}\sin\frac{\beta}{2}\cos\frac{\gamma}{2}+\sin\frac{\alpha}{2}\cos\frac{\beta}{2}\sin\frac{\gamma}{2}
\\ \cos\frac{\alpha}{2}\cos\frac{\beta}{2}\sin\frac{\gamma}{2}-\sin\frac{\alpha}{2}\sin\frac{\beta}{2}\cos\frac{\gamma}{2}
\end{bmatrix}$$

 　　根据上面的公式可以求出逆解，即由四元数$q=(q_0,q_1,q_2,q_3)$或$q=(w,x,y,z)$到欧拉角的转换为：

$$\begin{bmatrix}\alpha\\ \beta\\ \gamma\end{bmatrix} = \begin{bmatrix}
\arctan\frac{2(q_0q_1+q_2q_3)}{1-2(q_1^2+q_2^2)}\\
\arcsin(2(q_0q_2-q_1q_3))\\
\arctan\frac{2(q_0q_3+q_1q_2)}{1-2(q_2^2+q_3^2)}
\end{bmatrix}$$

　　由于arctan和arcsin的取值范围在$\frac{-\pi}{2}$和$\frac{\pi}{2}$之间，只有180°，而绕某个轴旋转时范围是360°，因此要使用atan2函数代替arctan函数：

$$\begin{bmatrix}\alpha\\ \beta\\ \gamma\end{bmatrix} = \begin{bmatrix}
atan2(2(q_0q_1+q_2q_3),1-2(q_1^2+q_2^2))\\
\arcsin(2(q_0q_2-q_1q_3))\\
atan2(2(q_0 q_3+q_1 q_2),1-2(q_2^2+q_3^2))
\end{bmatrix}$$

对于tan(θ) = y / x ：

　　θ = ATan(y / x)求出的θ取值范围是[-PI/2, PI/2]；

　　θ = ATan2(y, x)求出的θ取值范围是[-PI,   PI]。

• 当 (x, y) 在第一象限, 0 < θ < PI/2

• 当 (x, y) 在第二象限 PI/2 < θ≤PI

• 当 (x, y) 在第三象限, -PI < θ < -PI/2

• 当 (x, y) 在第四象限, -PI/2 < θ < 0

 　　将四元数转换为欧拉角可以参考下面的代码。需要注意欧拉角有12种旋转次序，而上面推导的公式是按照Z-Y-X顺序进行的，所以有时会在网上看到不同的转换公式（因为对应着不同的旋转次序），在使用时一定要注意旋转次序是什么。比如ADAMS软件里就默认Body 3-1-3次序，即Z-X-Z欧拉角，而VREP中则按照X-Y-Z欧拉角旋转。

enum RotSeq{zyx, zyz, zxy, zxz, yxz, yxy, yzx, yzy, xyz, xyx, xzy,xzx};

// COMPILE: g++ -o quat2EulerTest quat2EulerTest.cpp
#include <iostream>
#include <cmath> 

using namespace std;

///////////////////////////////
// Quaternion struct
// Simple incomplete quaternion struct for demo purpose
///////////////////////////////
struct Quaternion{
  Quaternion():x(), y(), z(), w(){};
  Quaternion(double x, double y, double z, double w):x(x), y(y), z(z), w(w){};

  void normalize(){
    double norm = std::sqrt(x*x + y*y + z*z + w*w);
    x /= norm;
    y /= norm;
    z /= norm;
    w /= norm;
  }

  double norm(){
    return std::sqrt(x*x + y*y + z*z + w*w);
  }

  double x;
  double y;
  double z;
  double w;  

};

///////////////////////////////
// Quaternion to Euler
///////////////////////////////
enum RotSeq{zyx, zyz, zxy, zxz, yxz, yxy, yzx, yzy, xyz, xyx, xzy,xzx};

void twoaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
  res[] = atan2( r11, r12 );
  res[] = acos ( r21 );
  res[] = atan2( r31, r32 );
}

void threeaxisrot(double r11, double r12, double r21, double r31, double r32, double res[]){
  res[] = atan2( r31, r32 );
  res[] = asin ( r21 );
  res[] = atan2( r11, r12 );
}

void quaternion2Euler(const Quaternion& q, double res[], RotSeq rotSeq)
{
    switch(rotSeq){
    case zyx:
      threeaxisrot( *(q.x*q.y + q.w*q.z),
                     q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                    -*(q.x*q.z - q.w*q.y),
                     *(q.y*q.z + q.w*q.x),
                     q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                     res);
      break;

    case zyz:
      twoaxisrot( *(q.y*q.z - q.w*q.x),
                   *(q.x*q.z + q.w*q.y),
                   q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                   *(q.y*q.z + q.w*q.x),
                  -*(q.x*q.z - q.w*q.y),
                  res);
      break;

    case zxy:
      threeaxisrot( -*(q.x*q.y - q.w*q.z),
                      q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                      *(q.y*q.z + q.w*q.x),
                     -*(q.x*q.z - q.w*q.y),
                      q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                      res);
      break;

    case zxz:
      twoaxisrot( *(q.x*q.z + q.w*q.y),
                  -*(q.y*q.z - q.w*q.x),
                   q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                   *(q.x*q.z - q.w*q.y),
                   *(q.y*q.z + q.w*q.x),
                   res);
      break;

    case yxz:
      threeaxisrot( *(q.x*q.z + q.w*q.y),
                     q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                    -*(q.y*q.z - q.w*q.x),
                     *(q.x*q.y + q.w*q.z),
                     q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                     res);
      break;

    case yxy:
      twoaxisrot( *(q.x*q.y - q.w*q.z),
                   *(q.y*q.z + q.w*q.x),
                   q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                   *(q.x*q.y + q.w*q.z),
                  -*(q.y*q.z - q.w*q.x),
                  res);
      break;

    case yzx:
      threeaxisrot( -*(q.x*q.z - q.w*q.y),
                      q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                      *(q.x*q.y + q.w*q.z),
                     -*(q.y*q.z - q.w*q.x),
                      q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                      res);
      break;

    case yzy:
      twoaxisrot( *(q.y*q.z + q.w*q.x),
                  -*(q.x*q.y - q.w*q.z),
                   q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                   *(q.y*q.z - q.w*q.x),
                   *(q.x*q.y + q.w*q.z),
                   res);
      break;

    case xyz:
      threeaxisrot( -*(q.y*q.z - q.w*q.x),
                    q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z,
                    *(q.x*q.z + q.w*q.y),
                   -*(q.x*q.y - q.w*q.z),
                    q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                    res);
      break;

    case xyx:
      twoaxisrot( *(q.x*q.y + q.w*q.z),
                  -*(q.x*q.z - q.w*q.y),
                   q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                   *(q.x*q.y - q.w*q.z),
                   *(q.x*q.z + q.w*q.y),
                   res);
      break;

    case xzy:
      threeaxisrot( *(q.y*q.z + q.w*q.x),
                     q.w*q.w - q.x*q.x + q.y*q.y - q.z*q.z,
                    -*(q.x*q.y - q.w*q.z),
                     *(q.x*q.z + q.w*q.y),
                     q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                     res);
      break;

    case xzx:
      twoaxisrot( *(q.x*q.z - q.w*q.y),
                   *(q.x*q.y + q.w*q.z),
                   q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z,
                   *(q.x*q.z + q.w*q.y),
                  -*(q.x*q.y - q.w*q.z),
                  res);
      break;
    default:
      std::cout << "Unknown rotation sequence" << std::endl;
      break;
   }
}

///////////////////////////////
// Helper functions
///////////////////////////////
Quaternion operator*(Quaternion& q1, Quaternion& q2){
  Quaternion q;
  q.w = q1.w*q2.w - q1.x*q2.x - q1.y*q2.y - q1.z*q2.z;
  q.x = q1.w*q2.x + q1.x*q2.w + q1.y*q2.z - q1.z*q2.y;
  q.y = q1.w*q2.y - q1.x*q2.z + q1.y*q2.w + q1.z*q2.x;
  q.z = q1.w*q2.z + q1.x*q2.y - q1.y*q2.x + q1.z*q2.w;
  return q;
}

ostream& operator <<(std::ostream& stream, const Quaternion& q) {
  cout << q.w << " "<< showpos << q.x << "i " << q.y << "j " << q.z << "k";
  cout << noshowpos;
}

double rad2deg(double rad){
  return rad*180.0/M_PI;
}

///////////////////////////////
// Main
///////////////////////////////
int main(){

  Quaternion q; // x,y,z,w
  Quaternion qx45(sin(M_PI/), ,, cos(M_PI/) );
  Quaternion qy45(, sin(M_PI/), , cos(M_PI/));
  Quaternion qz45(, , sin(M_PI/), cos(M_PI/));
  Quaternion qx90(sin(M_PI/), ,, cos(M_PI/) );
  Quaternion qy90(, sin(M_PI/), , cos(M_PI/));
  Quaternion qz90(, , sin(M_PI/), cos(M_PI/));

  double res[];

  q = qz45*qx45;
  q.normalize();
  quaternion2Euler(q, res, zyx);
  cout << "Rotation sequence: X->Y->Z" << endl;
  cout << "x45 -> z45" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[]) << " y: " << rad2deg(res[]) << " z: " << rad2deg(res[]) << endl << endl;

  q = qz90*qx90;
  q.normalize();
  quaternion2Euler(q, res, zyx);
  cout << "Rotation sequence: X->Y->Z" << endl;
  cout << "x90 -> z90" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[]) << " y: " << rad2deg(res[]) << " z: " << rad2deg(res[]) << endl << endl;

  q = qx90*qz90;
  q.normalize();
  quaternion2Euler(q, res, xyz);
  cout << "Rotation sequence: Z->Y->X" << endl;
  cout << "z90 -> x90" << endl;
  cout << "q: " << q << endl;
  cout << "x: " << rad2deg(res[]) << " y: " << rad2deg(res[]) << " z: " << rad2deg(res[]) << endl;
}

　　 上面的代码存在一个问题，即奇异性没有考虑。下面看一种特殊的情况（参考Maths - Conversion Quaternion to Euler）：假设一架飞机绕Y轴旋转了90°（俯仰角pitch=90），机头垂直向上，此时如何计算航向角和横滚角？

　　这时会发生自由度丢失的情况，即Yaw和Roll会变为一个自由度。此时再使用上面的公式根据四元数计算欧拉角会出现问题：

　　$\arcsin(2(q_0q_2-q_1q_3))$的定义域为$[-1,1]$，因此$(q_0q_2-q_1q_3)\in[-0.5, 0.5]$，当$q_0q_2-q_1q_3=0.5$时（在程序中浮点数不能直接进行等于判断，要使用合理的阈值），俯仰角$\beta$为90°，将其带入正向公式计算出四元数$(q_0,q_1,q_2,q_3)$，然后可以发现逆向公式中atan2函数中的参数全部为0，即出现了$\frac{0}{0}$的情况！无法计算。

　　$\beta=\pi/2$时，$\sin\frac{\beta}{2}=\cos\frac{\beta}{2}=0.707$，将其带入公式中有

$$q=\begin{bmatrix}w\\ x\\ y\\ z\end{bmatrix}
\begin{bmatrix}
0.707(\cos\frac{\alpha}{2}\cos\frac{\gamma}{2}+\sin\frac{\alpha}{2}\sin\frac{\gamma}{2})\\
0.707(\sin\frac{\alpha}{2}\cos\frac{\gamma}{2}-\cos\frac{\alpha}{2}\sin\frac{\gamma}{2})\\
0.707(\cos\frac{\alpha}{2}\cos\frac{\gamma}{2}+\sin\frac{\alpha}{2}\sin\frac{\gamma}{2})\\
0.707(\cos\frac{\alpha}{2}\sin\frac{\gamma}{2}-\sin\frac{\alpha}{2}\cos\frac{\gamma}{2})
\end{bmatrix}=
\begin{bmatrix}
0.707\cos\frac{\alpha-\gamma}{2}\\
0.707\sin\frac{\alpha-\gamma}{2}\\
0.707\cos\frac{\alpha-\gamma}{2}\\
0.707\sin\frac{\alpha-\gamma}{2}
\end{bmatrix}$$

　　则$\frac{x}{w}=\frac{z}{y}=\tan\frac{\alpha-\gamma}{2}$，于是有

$$\alpha-\gamma = 2\cdot atan2(x,w)$$

　　通常令$\alpha=0$，这时$\gamma = -2\cdot atan2(x,w)$。可以进行验证：当四元数为(w,x,y,z)=(0.653,-0.271,0.653,0.271)时，根据这些规则计算出来的ZYX欧拉角为α=0°，β=90°，γ=45°

　　当俯仰角为-90°，即机头竖直向下时的情况也与之类似，可以推导出奇异姿态时的计算公式。比较完整的四元数转欧拉角（Z-Y-X order）的代码如下：

CameraSpacePoint QuaternionToEuler(Vector4 q) // Z-Y-X Euler angles
{
    CameraSpacePoint euler = {  };
    const double Epsilon = 0.0009765625f;
    const double Threshold = 0.5f - Epsilon;

    double TEST = q.w*q.y - q.x*q.z;

    if (TEST < -Threshold || TEST > Threshold) // 奇异姿态,俯仰角为±90°
    {
        int sign = Sign(TEST);

        euler.Z = - * sign * (double)atan2(q.x, q.w); // yaw

        euler.Y = sign * (PI / 2.0); // pitch

        euler.X = ; // roll

    }
    else
    {
        euler.X = atan2( * (q.y*q.z + q.w*q.x), q.w*q.w - q.x*q.x - q.y*q.y + q.z*q.z);
        euler.Y = asin(- * (q.x*q.z - q.w*q.y));
        euler.Z = atan2( * (q.x*q.y + q.w*q.z), q.w*q.w + q.x*q.x - q.y*q.y - q.z*q.z);
    }

    return euler;
}

---

　　在DirectXMath Library中有许多与刚体姿态变换相关的函数可以直接调用：

• 四元数乘法：XMQuaternionMultiply method --Computes the product of two quaternions.
• 旋转矩阵转四元数：XMQuaternionRotationMatrix method --Computes a rotation quaternion from a rotation matrix.
• 四元数转旋转矩阵：XMMatrixRotationQuaternion method -- Builds a rotation matrix from a quaternion.
• 欧拉角转四元数：XMQuaternionRotationRollPitchYaw method --Computes a rotation quaternion based on the pitch, yaw, and roll (Euler angles).
• 四元数转Axis-Angle：XMQuaternionToAxisAngle method --Computes an axis and angle of rotation about that axis for a given quaternion.
• 欧拉角转旋转矩阵：XMMatrixRotationRollPitchYaw method --Builds a rotation matrix based on a given pitch, yaw, and roll (Euler angles).
• Axis-Angle转旋转矩阵：XMMatrixRotationAxis method --Builds a matrix that rotates around an arbitrary axis.
• 构造绕X/Y/Z轴的旋转矩阵：XMMatrixRotationX method --Builds a matrix that rotates around the x-axis.(Angles are measured clockwise when looking along the rotation axis toward the origin)

　　下面的代码中坐标系绕X轴旋转90°（注意这里不是按照右手定则的方向，而是沿着坐标轴向原点看过去以顺时针方式旋转，因此与传统的右手定则刚好方向相反），来进行变换：

#include "stdafx.h"
#include<iostream>

#include <DirectXMath.h>
using namespace DirectX;

#define PI 3.1415926

int _tmain(int argc, _TCHAR* argv[])
{
    //-------------------Computes the product of two quaternions.
    XMVECTOR q1 = XMVectorSet(, , , );
    XMVECTOR q2 = XMVectorSet(, , , );
    XMVECTOR q3 = XMVectorSet(, , , );

    XMVECTOR result = XMQuaternionMultiply(XMQuaternionMultiply(q3, q2), q1);   // Returns the product of two quaternions as q1*q2*q3

    std::cout << "Quaternion Multiply:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;

    //------------------Computes a rotation quaternion based on the pitch, yaw, and roll (Euler angles).
    float pitch = 90.0 * PI / 180.0; // Angle of rotation around the x-axis, in radians.
    float yaw = ;                     // Angle of rotation around the y-axis, in radians.
    float roll = ;                     // Angle of rotation around the z - axis, in radians.

    result = XMQuaternionRotationRollPitchYaw(pitch, yaw, roll);

    std::cout << "RPY/Euler angles to Quaternion:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;

    //-----------------Computes a rotation quaternion from a rotation matrix.
    float matrix[] = { , , , ,   , , , ,   , -, , ,   , , ,  };
    XMMATRIX trans(matrix); // Initializes a new instance of the XMMATRIX structure from a sixteen element float array.

    result = XMQuaternionRotationMatrix(trans); // This function only uses the upper 3x3 portion of the XMMATRIX.

    std::cout << "Matrix to Quaternion:" << std::endl;
    std::cout << XMVectorGetX(result) << "," << XMVectorGetY(result) << "," << XMVectorGetZ(result) << "," << XMVectorGetW(result) << std::endl << std::endl;

    //-----------------Builds a rotation matrix from a quaternion.
    trans = XMMatrixRotationQuaternion(result);

    XMFLOAT3X3 fView;
    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Quaternion to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;

    //-----------------Computes an axis and angle of rotation about that axis for a given quaternion.
    float Angle = ;
    XMVECTOR Axis;

    XMQuaternionToAxisAngle(&Axis, &Angle, result);

    Axis = XMVector3Normalize(Axis); // Returns the normalized version of a 3D vector
    std::cout << "Quaternion to Axis-Angle:" << std::endl;
    std::cout << "Axis: " << XMVectorGetX(Axis) << "," << XMVectorGetY(Axis) << "," << XMVectorGetZ(Axis) << std::endl;
    std::cout << "Angle: " << Angle*180.0 / PI << std::endl << std::endl;

    //-----------------Builds a matrix that rotates around an arbitrary axis.
    Angle = 90.0 * PI / 180.0;

    trans = XMMatrixRotationAxis(Axis, Angle);

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Axis-Angle to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
              << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
              << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;

    //-----------------Builds a rotation matrix based on a given pitch, yaw, and roll(Euler angles).
    trans = XMMatrixRotationRollPitchYaw(pitch, yaw, roll);

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "RPY/Euler angles to Matrix:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;

    //-----------------Builds a matrix that rotates around the x - axis.
    trans = XMMatrixRotationX(Angle); // Angles are measured clockwise when looking along the rotation axis toward the origin.

    XMStoreFloat3x3(&fView, trans); // Stores an XMMATRIX in an XMFLOAT3X3
    std::cout << "Builds a matrix that rotates around the x-axis.:" << std::endl;
    std::cout << fView._11 << "," << fView._12 << "," << fView._13 << std::endl
        << fView._21 << "," << fView._22 << "," << fView._23 << std::endl
        << fView._31 << "," << fView._32 << "," << fView._33 << std::endl << std::endl;

    return ;
}

　　结果如下图所示:

 

参考：

quaternions.online

DirectXMath Library Quaternion Functions

Convert quaternion to euler rotations

Conversion between quaternions and Euler angles

Maths - Conversion Quaternion to Euler

Coordinate Transformations in Robotics—MATLAB

Introduction to Robotics - Mechanics and Control. Chapter 2 Spatial descriptions and transformations