运筹学之"概率"和"累计概率"和"谁随机数"
概率 = 2/50 = 0.2
累计概率 = 上个概率加本次概率
案例1

概率=销量天数 / 天数 = 2 /100 = 0.02
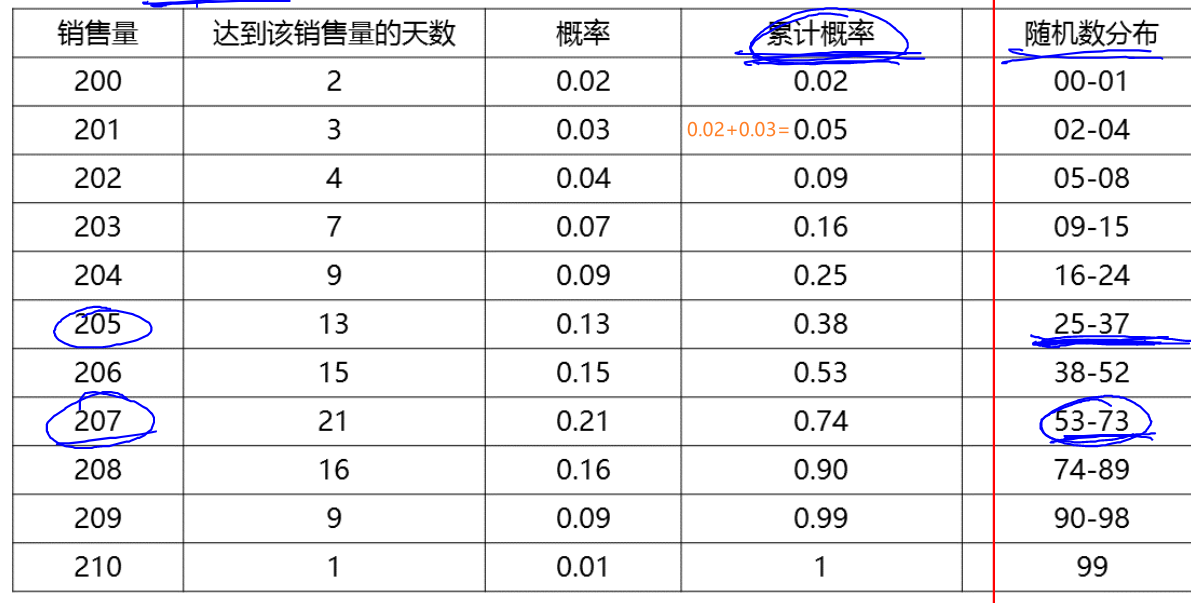
累计概率 = 上个概率加本次概率 = 0.02 +0.03 = 0.05
随机数分布=累计概率整值-1 =2 - 1 = 01
(因累计概率= 0.02 所以整数为2,公式=累计概率整值-1=2 - 1 = 1 所以等是00-01)
(因累计概率= 0.05 所以整数为5,公式=累计概率整值-1=5 - 1 = 4 所以等是02-04)

运筹学之"概率"和"累计概率"和"谁随机数"的更多相关文章
- BZOJ_3566_[SHOI2014]概率充电器_概率+树形DP
BZOJ_3566_[SHOI2014]概率充电器_概率+树形DP Description 著名的电子产品品牌 SHOI 刚刚发布了引领世界潮流的下一代电子产品——概率充电器: “采用全新纳米级加工技 ...
- luogu P4284 [SHOI2014]概率充电器 期望 概率 树形dp
LINK:概率充电器 大概是一个比较水的题目 不过有一些坑点. 根据期望的线性性 可以直接计算每个元件的期望 累和即为答案. 考虑统计每一个元件的概率的话 那么对其有贡献就是儿子 父亲 以及自己. 自 ...
- 67. 总结篇:面试中随机数"等概率"vs"不等概率"生成问题[random generator with equal or unequal probability]
[本文链接] http://www.cnblogs.com/hellogiser/p/random-generator-with-equal-or-unequal-probability.html 1 ...
- HDU-4089 Activation (概率DP求概率)
题目大意:一款新游戏注册账号时,有n个用户在排队.每处理一个用户的信息时,可能会出现下面四种情况: 1.处理失败,重新处理,处理信息仍然在队头,发生的概率为p1: 2.处理错误,处理信息到队尾重新排队 ...
- [SHOI2014]概率充电器(概率+换根dp)
著名的电子产品品牌SHOI 刚刚发布了引领世界潮流的下一代电子产品—— 概率充电器: “采用全新纳米级加工技术,实现元件与导线能否通电完全由真随机数决 定!SHOI 概率充电器,您生活不可或缺的必需品 ...
- BZOJ3566: [SHOI2014]概率充电器 树形+概率dp
3566: [SHOI2014]概率充电器 Time Limit: 40 Sec Memory Limit: 256 MBSubmit: 1888 Solved: 857[Submit][Stat ...
- CoderForce 148D-Bag of mice (概率DP求概率)
题目大意:美女与野兽在玩画鸽子的游戏.鸽子在用黑布遮住的笼子里,白色的有w只,黑色的有b只,每次拿出一只作画,谁先画到白色的鸽子谁就赢.美女首先画,因为野兽太丑,它每次画的时候都会吓跑一只鸽子,所有出 ...
- 2018.08.31 bzoj3566: [SHOI2014]概率充电器(概率dp+容斥原理)
传送门 概率dp好题啊. 用f[i]" role="presentation" style="position: relative;">f[i] ...
- 【BZOJ 3566】 3566: [SHOI2014]概率充电器 (概率树形DP)
3566: [SHOI2014]概率充电器 Description 著名的电子产品品牌 SHOI 刚刚发布了引领世界潮流的下一代电子产品——概率充电器:“采用全新纳米级加工技术,实现元件与导线能否通电 ...
随机推荐
- 【C# .Net GC】后台垃圾回收
在后台垃圾回收 (GC) 中,在进行第 2 代回收的过程中,将会根据需要收集暂时代(第 0 代和第 1 代). 后台垃圾回收是在一个或多个专用线程上执行的,具体取决于它是后台还是服务器 GC,它只适用 ...
- 利用Node.js编写跨平台的spawn语句
node const child = cp.spawn('npm', ['run', 'build']); 报错 events.js:182 throw er; // Unhandled 'error ...
- linux /etc/fstab 文件详细说明(整理版)
转至:https://blog.csdn.net/xiaolongwang2010/article/details/8657332?utm_medium=distribute.pc_relevant. ...
- Weblogic补丁升级常见问题
转至:https://blog.csdn.net/weixin_44659716/article/details/106804177 常用企业级版本:Weblogic 11g(weblogic10.3 ...
- mapreduce—shuffle图解
- Qt:QByteArray
0.说明 QByteArray是存储二进制byte数组. 区别于QString:QByteArray中存储的全是byte,而QString中存储的全是16 bit Unicode码.QString是在 ...
- [翻译] TensorFlow 分布式之论文篇 "TensorFlow : Large-Scale Machine Learning on Heterogeneous Distributed Systems"
[翻译] TensorFlow 分布式之论文篇 "TensorFlow : Large-Scale Machine Learning on Heterogeneous Distributed ...
- vue 控制台错误
控制台显示报错: Uncaught TypeError: WEBPACK_IMPORTED_MODULE_1_vuex.a.store is not a constructor 解决办法: 将new ...
- 面试官:Redis集群有哪些方式,Leader选举又是什么原理呢?
哈喽!大家好,我是小奇,一位不靠谱的程序员 小奇打算以轻松幽默的对话方式来分享一些技术,如果你觉得通过小奇的文章学到了东西,那就给小奇一个赞吧 文章持续更新 一.前言 作为一名Java程序员,Redi ...
- 【工程应用五】 opencv中linemod模板匹配算法诸多疑惑和自我解读。
研究这个前前后后也有快两三个月了,因为之前也一直在弄模板匹配方面的东西,所以偶尔还是有不少朋友咨询或者问你有没有研究过linemod这个算法啊,那个效率啥的还不错啊,有段时间一直不以为然,觉得我现在用 ...
