通过有序线性结构构造AVL树

通过有序线性结构构造AVL树

本博客旨在结局利用有序数组和有序链表构造平衡二叉树（下文使用AVL树代指）问题。

直接通过旋转来构造AVL树似乎是一个不错的选择，但是稍加分析就会发现，这样平白无故做了许多毫无意义的旋转。因为直接通过旋转调整二叉查找树（下文使用BST代指）并没有利用数组或链表本身是有序的信息，进行了大量无意义的操作。

下面通过leetcode两道例题来说明这个问题。

1. 108. 将有序数组转换为二叉搜索树

题目分析

重点的问题在于：如何利用数组的有序信息呢？

首先我们先来观察一个有序数组和一棵AVL树所呈现的关系

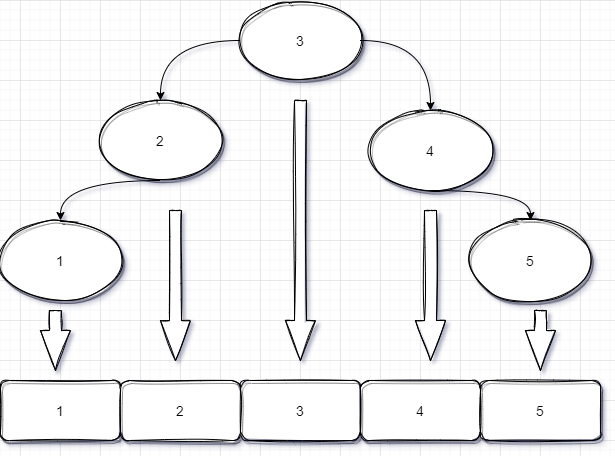
我们可以发现数组中间元素恰好是对应AVL树的root节点（若数组长为偶数，可取中间偏左或偏右元，此时左右子树高度差为1）

我们只需要选取中间元素，构造头节点，在递归地构造其左右子树即可。

代码实现与说明

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    private TreeNode build(int[] nums, int l, int r) {
        // 为什么采用l小于r而不是等于来判断呢？
        // 我们这里是采用的闭区间的写法，当然可以采用闭开区间的写法，也就是等于时返回null
        // 循环和递归函数的边界条件一定要多加注意
        if (l > r)
            return null;
        // 防止因为l和r过大造成溢出，不过这道题数组长度不会那么大，但最好还是养成这样的习惯
        int mid = l + (r - l) / 2;
        // 其实这是一个中序遍历，先建立root节点，在递归地建立左子树和右子树
        TreeNode node = new TreeNode(nums[mid]);
        node.left = build(nums, l, mid - 1);
        node.right = build(nums, mid + 1, r);
        // 建立好后返回root节点即可
        return node;
    }
}

递归函数是如何设计的呢？

1. 参数：我们需要访问nums数组元素，因此需要将其传入函数，也可以在Solution类中设计一个实例变量引用nums数组。同时，为例确定中间元素，我们需要明确数组的左右边界，因此传入参数l和r，它们也是判断数组内是否还有元素用来建立AVL树节点，也就是说当l小于r时，返回null节点。
2. 返回值：这个比较显而易见，我们需要递归函数返回一个TreeNode节点（或者说它是已构造好子树的头节点）。

复杂度分析

时间复杂度：这道题本质上是使用先序遍历的方式构造一棵树，每个节点都被构造一次且路过三次，所以时间复杂度显然为O(N)

空间复杂度：递归调用栈深度为树的深度，由于构造的树为AVL树，其深度不超过lg(N)，递归调用栈深度也不超过O(lgN)，故空间复杂度为O(lgN)

2. 109. 有序链表转换二叉搜索树

题目分析

这道题是108题的兄弟版本，数组可以随机访问元素，因此我们可以轻而易举地得到中间元素，但是链表不再具备这个特性。因此我们需要采取其他的方法来解决这个问题。

1. 将链表元素依次取出，构造出一个有序数组，再利用108的方法去做。不过空间复杂度提升为O(N)
2. 采用快慢指针法取出中间节点，但是每次构造子树root节点均需使用快慢指针法，导致时间复杂度会降低为O(lgN)
3. 更优秀的方法：利用AVL树中序遍历生成的序列即为所给有序链表这一性质，采用中序遍历构造AVL树，兼具方法1和方法2的优点

代码实现与说明

方法1不给出代码，其实相比于108题只是多了一步构造数组罢了。

方法2代码

class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        return build(head, null);
    }
    private TreeNode build(ListNode l, ListNode r) {
        if (l == r)
            return null;
        ListNode slow = l, fast = slow;
        // 快慢指针寻找中间节点，可以说是本做法的核心，注意循环的条件
        while (fast != r && fast.next != r) {
            slow = slow.next;
            fast = fast.next.next;
        }
        // 其实这是一个先序遍历的过程，在过程AVL树
        TreeNode node = new TreeNode(slow.val);
        node.left = build(l, slow);
        node.right = build(slow.next, r);
        return node;
    }
}

递归函数设计说明:

1. 返回值：返回值显然要返回树节点，因为我们需要向上一级调用函数返回构造好子树的头节点
2. 参数：本函数参数选择是重中之重，向上面代码所示选用闭开区间的写法可以避免一些麻烦，不要忘记这是个单链表，如写成闭区间的模式，那么需要额外的prev指针来指示slow指针的前一个元素（对照108的代码去看)

方法2缺陷：快慢指针寻找中间元素所需时间复杂度是o(lgN)，我们每次在构造子树root节点时均需要使用它一次，这无疑造成了一些浪费。让我们回到108题所示图片中（把那个数组想象为一个链表），AVL树中序遍历产生的序列与链表是一致的。可以利用这个特点改进方法2吗？

方法3思路说明：

这里附上一份详细的参考链接

https://leetcode.cn/problems/convert-sorted-list-to-binary-search-tree/solution/shou-hua-tu-jie-san-chong-jie-fa-jie-zhu-shu-zu-ku/

方法3代码

class Solution {
    // 递归过程中各个函数均维护一个链表头，故将其设为实例变量
    ListNode listHead;
    public TreeNode sortedListToBST(ListNode head) {
        listHead = head;
        int length = getLength(head);
        return build(0, length - 1);
    }
    // 一定要多注意该函数参数的设计，参数是整数索引！不再像方法2那样是ListNode引用
    // 一定要好好理解这个函数
    private TreeNode build(int left, int right) {
        if (left > right)
            return null;
        TreeNode node = new TreeNode();
        int mid = left + (right - left) / 2;
        node.left = build(left, mid - 1);
        node.val = listHead.val;
        listHead = listHead.next;
        node.right = build(mid + 1, right);
        return node;
    }
    // 辅助函数，作用是遍历链表，统计其长度
    private int getLength(ListNode head) {
        int counter = 0;
        while (head != null) {
            counter++;
            head = head.next;
        }
        return counter;
    }
}

递归函数的说明：

1. 参数设计：有些人（包括我在内）开始可能很诧异为什么不像方法2一样使ListNode作为参数呢？不要忘记，一旦参数使用ListNode那不就变成方法2了嘛，无法直接访问中间元素。要想直接访问中间元，就要使用整数索引。
2. 如何理解递归函数的流程：最好的方法就是逐行分析代码，尝试模拟运行。不过这里还是给出一些说明，首先我们先建立node节点，先递归地建立其左子树，然后将链表头listHead指向下一个元素，此时listHead指向的节点恰好为中间节点，我们取出它的值，再递归地建立其右子树。