Python实现改进后的Bi-RRT算法实例

Python实现改进后的Bi-RRT算法实例

1.背景说明

以下代码是参照上海交通大学海洋工程国家重点实验室《基于改进双向RRT的无人艇局部路径规划算法研究》的算法思想实现的。

2.算法流程

1. 产生随机节点pi
2. 寻找T1中距离p1最近的节点pn
3. 以pn为父节点按原始步长向pi延伸得到虚新节点pa
4. 确定距离pi最近的障碍物
5. 使用动态步长策略计算实际步长sf
6. 按照实际sf延伸得到实际节点新pw
7. 障碍物检测 通过则进入步骤8 否则重回步骤1
8. 转角约束检测 通过则进入步骤9 否则重回步骤1
9. 将pw加入T1
10. 在T2中寻找距离pw最近的节点pj
11. 以pj为父节点按原始步长向pw延伸得到虚新节点pb
12. 确定距离pb最近的障碍物
13. 使用动态步长策略计算实际步长sf
14. 按照实际sf延伸得到实际新节点px
15. 障碍物检测 通过则进入步骤16 否则重回步骤1
16. 转角约束检测 通过则进入步骤17 否则重回步骤1
17. 将pw加入T2
18. 检测是否满足相遇条件 是则进入步骤20 否则继续步骤1
19. 检测是否满足平滑连接 是则结束搜索 否则继续步骤1
20. 路径回溯

3.实际代码

"""
基于改进双向RRT算法的路径规划
"""
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import numpy as np
import math
import random
import copy

class Point(object):
    """
    路径节点
    """

    def __init__(self, x, y):
        self.x = x
        self.y = y
        self.parent = None

class BiRRT(object):
    """
    双向RRT算法实现
    """

    def __init__(self, start, goal, angle, step, distance, obstacle_list, rand_area, safe, recover):
        """
        初始化
        :param start: 起点 [x,y]
        :param goal: 终点 [x,y]
        :param angle: 转向角 60
        :param step: 基础步长 10
        :param obstacle_list: 障碍物列表 [[x,y,radius]...]
        :param rand_area: 区域大小
        :param safe: 安全航迹结束点
        :param recover: 安全航迹恢复点
        """
        self.start = Point(start[0], start[1])
        self.goal = Point(goal[0], goal[1])
        self.angle = angle
        self.step = step
        self.distance = distance
        self.obstacle_list = obstacle_list
        self.min_rand = rand_area[0]
        self.max_rand = rand_area[1]
        self.goalSampleRate = 0.05
        self.safe = Point(safe[0], safe[1])
        self.recover = Point(recover[0], recover[1])
        # 从起点开始搜索
        self.point_list_from_start = [self.start]
        begin = copy.deepcopy(self.safe)
        begin.parent = 0
        self.point_list_from_start.append(begin)

        # 从终点开始搜索
        self.point_list_from_goal = [self.goal]
        begin = copy.deepcopy(self.recover)
        begin.parent = 0
        self.point_list_from_goal.append(begin)

    def random_point(self):
        """
        产生随机节点
        :return:
        """
        point_x = random.uniform(self.safe.x, self.recover.y)
        point_y = random.uniform(self.safe.x, self.recover.y)
        point = [point_x, point_y]
        return point

    @staticmethod
    def get_nearest_list_index(point_list, rnd):
        """
        在节点列表中找到距离目标节点中最近的点
        :param point_list: 节点列表 T1 or obstacle_list
        :param rnd: 目标节点
        :return: 最近节点的位置
        """
        d_list = [(point.x - rnd[0]) ** 2 + (point.y - rnd[1]) ** 2 for point in point_list]
        min_index = d_list.index(min(d_list))
        return min_index

    def get_nearest_obstacle_index(self, point):
        """
        找到距离point最近的障碍物
        :param point: 节点
        :return: 最近的障碍物
        """
        d_list = [(math.sqrt((point.x - x) ** 2 + (point.y - y) ** 2)) - r for (x, y, r) in self.obstacle_list]
        min_index = d_list.index(min(d_list))
        return min_index

    def collision_check(self, t, new_point, obstacle_list):
        """
        检查新的节点是否会碰撞或穿越到障碍物
        :param t: 树
        :param new_point: 实际新节点
        :param obstacle_list: 障碍物列表
        :return:
        """
        flag = 1
        for (ox, oy, radius) in obstacle_list:
            # 点到障碍物中心的距离
            dx = ox - new_point.x
            dy = oy - new_point.y
            d = math.sqrt(dx * dx + dy * dy)
            # 判断是否穿过障碍物
            if t == 1:
                parent_point = self.point_list_from_start[new_point.parent]
            else:
                parent_point = self.point_list_from_goal[new_point.parent]

            vector_o = np.array([ox, oy])
            vector_p = np.array([parent_point.x, parent_point.y])
            vector_n = np.array([new_point.x, new_point.y])
            d_p_n = np.abs(np.cross(vector_p - vector_o, vector_n - vector_o)) / np.linalg.norm(vector_p - vector_n)
            # 如果点落在或穿过障碍物
            if d < radius or d_p_n < radius:
                flag = 0
                return flag
        return flag

    def angle_check(self, new_point, parent_point, ancestor_point):
        """
        转角约束
        :param new_point: 新节点 w
        :param parent_point: n节点(新节点的父级节点)
        :param ancestor_point: f祖先节点
        :return:
        """
        vector_p_n = np.array([new_point.x - parent_point.x, new_point.y - parent_point.y])
        vector_a_p = np.array([parent_point.x - ancestor_point.x, parent_point.y - ancestor_point.y])
        angle = get_angle(vector_a_p, vector_p_n)
        if angle <= self.angle:
            return True
        else:
            return False

    def dynamic_step(self, n_point, a_point):
        """
        计算动态步长
        :param n_point: 父节点
        :param a_point: 虚新节点
        :return: Sf 动态步长
        """

        tan = math.atan2(a_point.y - n_point.y, a_point.x - n_point.x)
        a_point.x += math.cos(tan) * (self.distance + self.step) / 2
        a_point.y += math.sin(tan) * (self.distance + self.step) / 2
        # 距离最近的障碍物
        obstacle_min = self.obstacle_list[self.get_nearest_obstacle_index(a_point)]
        # 虚拟节点a_point至障碍物边缘的距离l_a
        l_a = math.sqrt((a_point.x - obstacle_min[0]) ** 2 + (a_point.y - obstacle_min[1]) ** 2) - obstacle_min[2]
        # 生长点n_point至障碍物边缘的距离l_n
        l_n = math.sqrt(np.square(n_point.x - obstacle_min[0]) + np.square(n_point.y - obstacle_min[1])) - obstacle_min[
            2]

        dynamic = self.step / (1 + (self.step / self.distance - 1) * math.exp(-3 * l_n / self.step))
        return dynamic

    def coordinate(self, t, rnd):
        """
        实际坐标计算
        :param t: 搜索树编号 1 2
        :param rnd: 虚新节点
        :return: 实际新节点
        """
        # 在搜索树中找到距离rnd最近的节点
        if t == 1:
            min_index = self.get_nearest_list_index(self.point_list_from_start, rnd)
            nearest_point = self.point_list_from_start[min_index]
        elif t == 2:
            min_index = self.get_nearest_list_index(self.point_list_from_goal, rnd)
            nearest_point = self.point_list_from_goal[min_index]

        # 按照原始步长计算坐标
        theta = math.atan2(rnd[1] - nearest_point.y, rnd[0] - nearest_point.x)
        new_point = copy.deepcopy(nearest_point)
        new_point.x += math.cos(theta) * self.step
        new_point.y += math.sin(theta) * self.step
        new_point.parent = min_index
        # 使用动态步长策略计算实际坐标
        actual_step = self.dynamic_step(nearest_point, new_point)
        new_point.x = nearest_point.x + math.cos(theta) * actual_step
        new_point.y = nearest_point.y + math.sin(theta) * actual_step
        return new_point, actual_step

    def condition_check(self, t, new_point):
        """
        限制条件检测
        1.碰撞检测
        2.转交约束检测
        :param t: 搜索树
        :param new_point: 实际新节点
        :return: Boolean
        """
        # 碰撞检测
        if self.collision_check(t, new_point, self.obstacle_list):
            if t == 1:  # 搜索树1的转角约束检测
                n_point = self.point_list_from_start[new_point.parent]
                if n_point.parent is None:
                    return False
                f_point = self.point_list_from_start[n_point.parent]
                if self.angle_check(new_point, n_point, f_point):
                    return True
                else:
                    return False
            else:  # 搜索树2的转角约束检测
                n_point = self.point_list_from_goal[new_point.parent]
                if n_point.parent is None:
                    return False
                f_point = self.point_list_from_goal[n_point.parent]
                if self.angle_check(new_point, n_point, f_point):
                    return True
                else:
                    return False
        else:
            return False

    def perfect_connect(self, one_point, two_point):
        """
        计算是否满足平滑连接
        :param one_point: 1号树的节点 w
        :param two_point: 2号树的节点 x
        :return:
        """
        one_parent = self.point_list_from_start[one_point.parent]  # n
        two_parent = self.point_list_from_goal[two_point.parent]  # j

        vector_n_w = np.array([one_point.x - one_parent.x, one_point.y - one_parent.y])
        vector_w_x = np.array([two_point.x - one_point.x, two_point.y - one_point.y])
        vector_x_j = np.array([two_parent.x - two_point.x, two_parent.y - two_point.y])

        angle_one = get_angle(vector_n_w, vector_w_x)
        angle_two = get_angle(vector_w_x, vector_x_j)
        if angle_one <= self.angle:
            if angle_two == 180.0 or angle_one == 0.0:
                return False
            else:
                print("phi: {0}, delta: {1}".format(angle_one, angle_two))
                return True
        else:
            return False

    def generate_path_list(self):
        """
        路径回溯
        :return: list
        """
        path = []
        path_1 = []
        path_2 = []
        last_index = len(self.point_list_from_start) - 1
        while self.point_list_from_start[last_index].parent is not None:
            point = self.point_list_from_start[last_index]
            path.append([point.x, point.y])
            path_1.append([point.x, point.y])
            last_index = point.parent
        path.append([self.start.x, self.start.y])
        path_1.append([self.start.x, self.start.y])
        path = path[::-1]
        last_index = len(self.point_list_from_goal) - 1
        while self.point_list_from_goal[last_index].parent is not None:
            point = self.point_list_from_goal[last_index]
            path.append([point.x, point.y])
            path_2.append([point.x, point.y])
            last_index = point.parent
        path.append([self.goal.x, self.goal.y])
        path_2.append([self.goal.x, self.goal.y])
        print("最终规划路径：", path)
        print("搜索树1：", path_1)
        print("搜索树2：", path_2)
        return path, path_1, path_2

    def planning(self):
        """
        路径规划算法的具体实现
        流程：
        1.产生随机节点pi
        2.寻找T1中距离p1最近的节点pn
        3.以pn为父节点按原始步长向pi延伸得到虚新节点pa
        4.确定距离pi最近的障碍物
        5.使用动态步长策略计算实际步长sf
        6.按照实际sf延伸得到实际节点新pw
        7.障碍物检测 通过则进入步骤8 否则重回步骤1
        8.转角约束检测 通过则进入步骤9 否则重回步骤1
        9.将pw加入T1
        10.在T2中寻找距离pw最近的节点pj
        11.以pj为父节点按原始步长向pw延伸得到虚新节点pb
        12.确定距离pb最近的障碍物
        13.使用动态步长策略计算实际步长sf
        14.按照实际sf延伸得到实际新节点px
        15.障碍物检测 通过则进入步骤16 否则重回步骤1
        16.转角约束检测 通过则进入步骤17 否则重回步骤1
        18.将pw加入T2
        19.检测是否满足相遇条件 是则进入步骤20 否则继续步骤1
        20.检测是否满足平滑连接 是则结束搜索 否则继续步骤1
        21.路径回溯
        :return: [[x, y]]
        """
        # 路径搜索
        while True:
            """
            搜索树1的实现
            """
            # T1产生随机节点
            if random.random() > self.goalSampleRate:
                rnd = self.random_point()
            else:
                rnd = [self.goal.x, self.goal.y]
            # 计算后的实际新节点和动态步长
            new_point, actual_step = self.coordinate(1, rnd)
            # 限制条件检测
            if not self.condition_check(1, new_point):
                continue
            # 实际新节点通过检测 加入T1
            self.point_list_from_start.append(new_point)
            """
            搜索树2的实现
            """
            # 实际新节点
            new_point_two, actual_step = self.coordinate(2, [new_point.x, new_point.y])
            # 限制条件检测
            if not self.condition_check(2, new_point_two):
                continue
            # 实际新节点加入 T2
            self.point_list_from_goal.append(new_point_two)
            """
            判断是否达到目标点
            """
            # 判断是否满足相遇条件
            dx = new_point.x - new_point_two.x
            dy = new_point.y - new_point_two.y
            d = math.sqrt(dx * dx + dy * dy)
            if self.distance < d < self.step:
                if self.perfect_connect(new_point, new_point_two):
                    break
                else:
                    continue
            else:
                continue
        return self.generate_path_list()

    def draw_statistic(self, path):
        """
        绘制静态图像
        :param path: 规划完成的路径
        :return:
        """
        plt.clf()

        # 绘制区域
        # x轴刻度区间
        x_major_location = MultipleLocator(10)
        # y轴刻度区间
        y_major_location = MultipleLocator(10)
        # 坐标轴实例
        ax = plt.gca()
        ax.xaxis.set_major_locator(x_major_location)
        ax.yaxis.set_major_locator(y_major_location)
        plt.axis([self.min_rand, self.max_rand, self.min_rand, self.max_rand])

        # 绘制障碍物
        for (ox, oy, radius) in self.obstacle_list:
            circle = plt.Circle(xy=(ox, oy), radius=radius, color="r")
            ax.add_patch(circle)

        # 绘制起点
        plt.plot(self.start.x, self.start.y, "^g")
        # 绘制终点
        plt.plot(self.goal.x, self.goal.y, "^b")

        # 绘制规划的路径
        plt.plot([data[0] for data in path], [data[1] for data in path], "-y")
        for (x, y) in path:
            plt.scatter(x, y, marker='o', c='b', edgecolors='b')

        ax.set_aspect('equal', adjustable='datalim')
        ax.plot()
        plt.grid(True)
        plt.show()

def get_angle(a, b):
    """
    向量夹角计算
    :param a:
    :param b:
    :return:
    """
    a_norm = np.sqrt(np.sum(a * a))
    b_norm = np.sqrt(np.sum(b * b))
    cos_value = float(np.dot(a, b) / (a_norm * b_norm))
    eps = 1e-6
    if 1.0 < cos_value < 1.0 + eps:
        cos_value = 1.0
    elif -1.0 - eps < cos_value < -1.0:
        cos_value = -1.0
    arc_value = np.arccos(cos_value)
    angle_value = arc_value * (180 / np.pi)
    return angle_value

def get_total_distance(path):
    """
    计算路径总长度
    :param path:
    :return:
    """
    total_distance = 0
    for index in range(2, len(path)-1):
        one = path[index-1]
        two = path[index]
        total_distance += np.sqrt(np.square(two[0] - one[0]) + np.square(two[1] - one[0]))
    print(total_distance)

def main():
    print("============================Start planning your path============================")
    rand_area = [0, 100]  # 区域大小
    step = 10  # 基础步长
    angle = 60  # 最大转向角
    distance = 5  # 最小航行距离
    start = [0, 0]  # 起点
    goal = [100, 100]  # 终点
    safe = [20, 20]
    recover = [90, 90]
    # 障碍物
    obstacle_list = [
        (50, 50, 15),
        (62, 13, 12),
        (50, 87, 11)
    ]
    bi_rrt = BiRRT(start=start, goal=goal, angle=angle, step=step, distance=distance, obstacle_list=obstacle_list,
                   rand_area=rand_area, safe=safe, recover=recover)
    path, path_1, path_2 = bi_rrt.planning()
    bi_rrt.draw_statistic(path)
    get_total_distance(path)
    print("==========================End of planned path==========================")

if __name__ == '__main__':
    main()

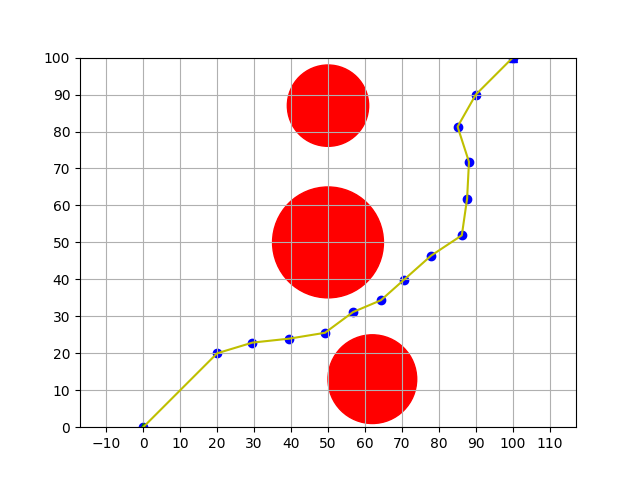
4. 效果图