Linux下C语言程序的内存布局

在《虚拟地址空间以及编译模式》一节中讲到，虚拟地址空间在32位环境下的大小为 4GB，在64位环境下的大小为 256TB，那么，一个C语言程序的内存在整个地址空间中是如何分布的呢？数据在哪里？代码在哪里？为什么要这样分布？这些就是本节要讲解的内容。

程序内存在地址空间中的分布情况称为内存模型（Memory Model）。内存模型由操作系统构建，在Linux和Windows下有所差异，并且会受到编译模式的影响，本节我们讲解Linux下32位环境和64位环境的内存模型。

内核空间和用户空间

对于32位环境，理论上程序可以拥有 4GB 的虚拟地址空间，我们在C语言中使用到的变量、函数、字符串等都会对应内存中的一块区域。

但是，在这 4GB 的地址空间中，要拿出一部分给操作系统内核使用，应用程序无法直接访问这一段内存，这一部分内存地址被称为内核空间（Kernel Space）。

Windows 在默认情况下会将高地址的 2GB 空间分配给内核（也可以配置为1GB），而 Linux 默认情况下会将高地址的 1GB 空间分配给内核。也就是说，应用程序只能使用剩下的 2GB 或 3GB 的地址空间，称为用户空间（User Space）。

Linux下32位环境的用户空间内存分布情况

我们暂时不关心内核空间的内存分布情况，下图是Linux下32位环境的一种经典内存模型：

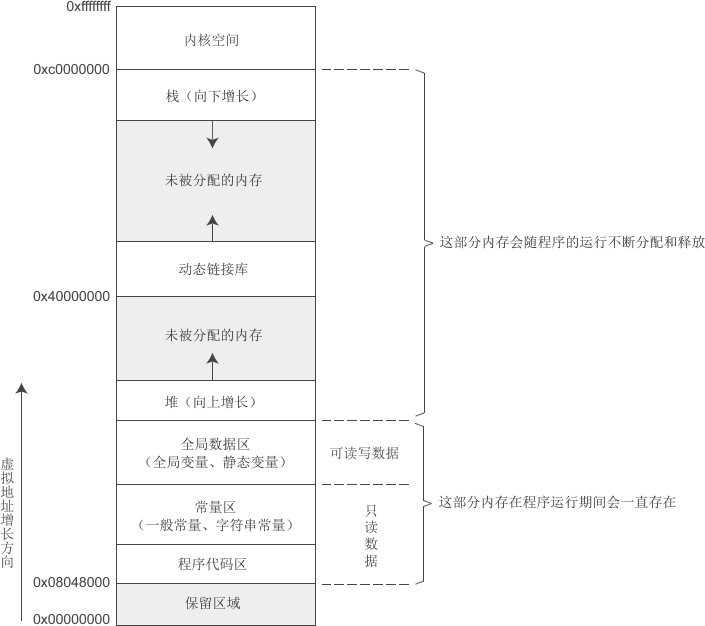
对各个内存分区的说明：

内存分区	说明
程序代码区 (code)	存放函数体的二进制代码。一个C语言程序由多个函数构成，C语言程序的执行就是函数之间的相互调用。
常量区 (constant)	存放一般的常量、字符串常量等。这块内存只有读取权限，没有写入权限，因此它们的值在程序运行期间不能改变。
全局数据区 (global data)	存放全局变量、静态变量等。这块内存有读写权限，因此它们的值在程序运行期间可以任意改变。
堆区 (heap)	一般由程序员分配和释放，若程序员不释放，程序运行结束时由操作系统回收。malloc()、calloc()、free() 等函数操作的就是这块内存，这也是本章要讲解的重点。 注意：这里所说的堆区与数据结构中的堆不是一个概念，堆区的分配方式倒是类似于链表。
动态链接库	用于在程序运行期间加载和卸载动态链接库。
栈区 (stack)	存放函数的参数值、局部变量的值等，其操作方式类似于数据结构中的栈。

在这些内存分区中（暂时不讨论动态链接库），程序代码区用来保存指令，常量区、全局数据区、堆、栈都用来保存数据。对内存的研究，重点是对数据分区的研究。

程序代码区、常量区、全局数据区在程序加载到内存后就分配好了，并且在程序运行期间一直存在，不能销毁也不能增加（大小已被固定），只能等到程序运行结束后由操作系统收回，所以全局变量、字符串常量等在程序的任何地方都能访问，因为它们的内存一直都在。

常量区和全局数据区有时也被合称为静态数据区，意思是这段内存专门用来保存数据，在程序运行期间一直存在。

函数被调用时，会将参数、局部变量、返回地址等与函数相关的信息压入栈中，函数执行结束后，这些信息都将被销毁。所以局部变量、参数只在当前函数中有效，不能传递到函数外部，因为它们的内存不在了。

常量区、全局数据区、栈上的内存由系统自动分配和释放，不能由程序员控制。程序员唯一能控制的内存区域就是堆（Heap）：它是一块巨大的内存空间，常常占据整个虚拟空间的绝大部分，在这片空间中，程序可以申请一块内存，并自由地使用（放入任何数据）。堆内存在程序主动释放之前会一直存在，不随函数的结束而失效。在函数内部产生的数据只要放到堆中，就可以在函数外部使用。