week_7

Andrew Ng 机器学习笔记 ---By Orangestar

Week_7

This week, you will be learning about the support vector machine (SVM) algorithm. SVMs are considered by many to be the most powerful 'black box' learning algorithm, and by posing a cleverly-chosen optimization objective, one of the most widely used learning algorithms today.

1. Optimization Objective

更加强大 的方法：支持向量机SVM（support vectors machine）

首先，我们需要从优化开始。

支持向量机(Support vector machine)通常用在机器学习 (Machine learning)。是一种监督式学习 (Supervised Learning)的方法，主要用在统计分类 (Classification)问题和回归分析 (Regression)问题上。其中SVM的代价函数如下所示：

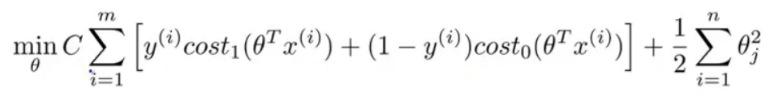
这个代价函数是由logistic regression变化过来的,只需将下图同时乘以m，除以λ即可得到SVM的代价函数。即SVM的损失函数的形式为CA+B，而逻辑回归损失函数的形式为A+\(\lambda\)B

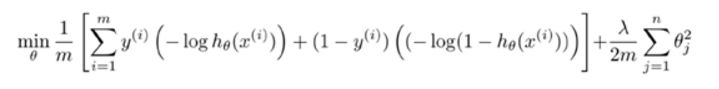
其中总结如下：

还有一个问题，是给第一项更大的权重还是第二项，可以通过不同的方式来选择正则项

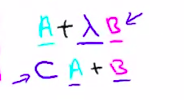
2. Large Margin Intuition

现在我们的代价函数变化了，所以我们想要的也稍微有些变化：

当然，对于正则项：

这样我们就会得到一个很有趣的决策界限

注意观察图像，黑色是最好的一条决策界限

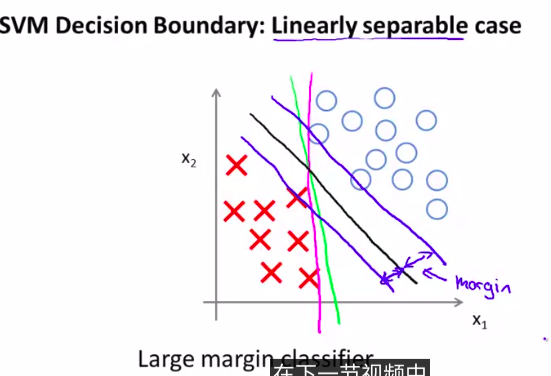
所以，支持向量机也可以叫做大间距分类器

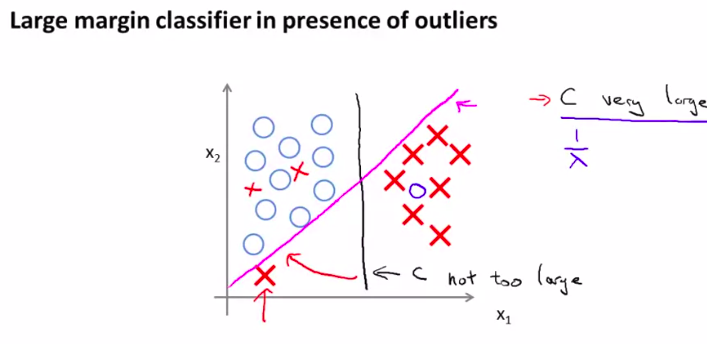
所以。正则化参数C的设置是非常关键的。如何处理这种参数的平衡？且听下回分解。

× 3. Mathematics Behind Large Margin Classification（optional）

为什么这样的代价函数就可以得到这样的大间距分类器，即支持向量机？

首先，我们先回顾一下向量内积的知识

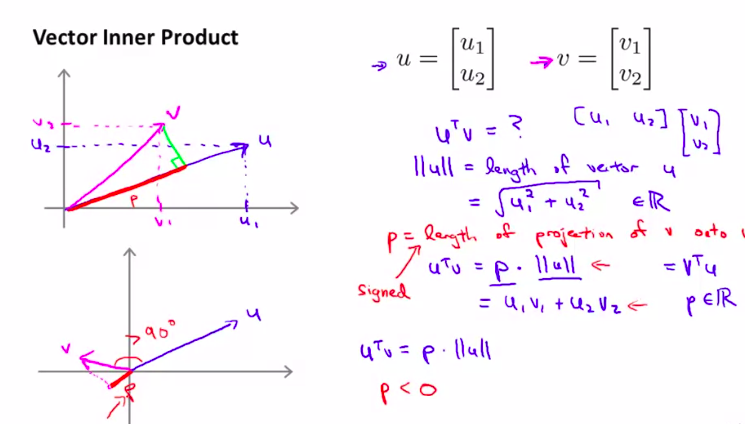
超级简单的回顾一哈。

然后，可以观察前面的项和正则化项的联系，通过向量的定义！

我们先简化计算，把\(\theta_0\)当做0来处理

为什么不会选择黄色线？

仔细想想向量点积的几何意义！如果这样的话，就会非常小！意思是\(\theta\)的范数会十分大！

然后对比一下右图的绿色线！

这样P和\(\theta\)相乘就变大了！！！

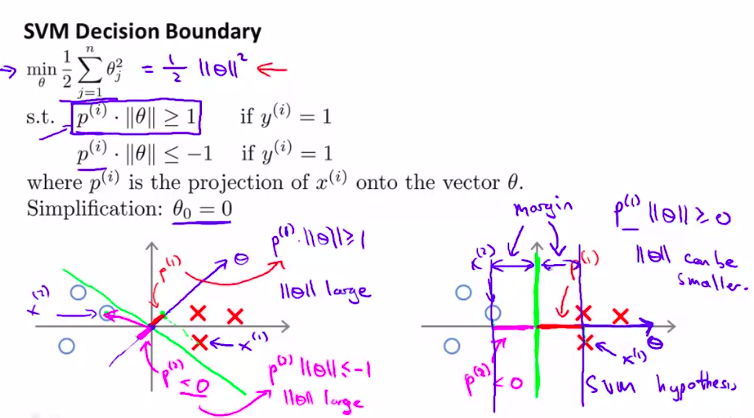
这样就得到了一个大间距分类器

（找到了一个\(\theta\)较小的范数）

当然，\(\theta_0\)也可以不为0.

但是无论如何，都会优化这个函数

4. Kernels I

构造浮躁的非线性分类器

使用kernels

核函数（也叫高斯核函数）

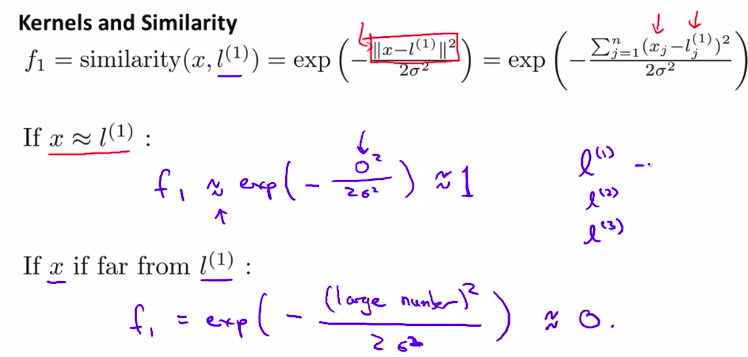
这是 相似度函数

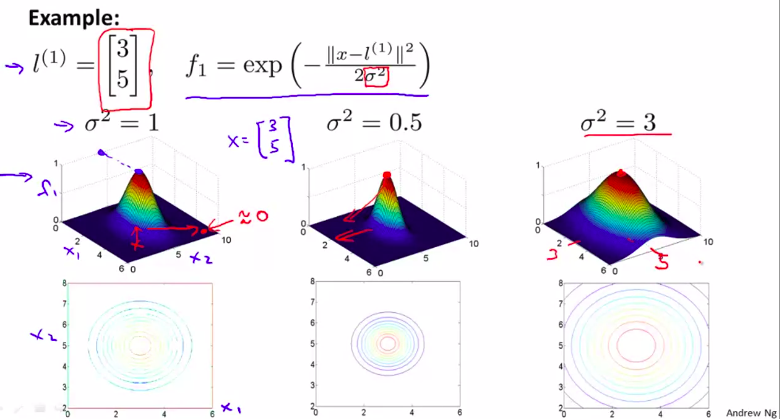
注意观察，当x越靠近l 的时候，函数值越接近于 0 。然后随着 \(\delta\)的变大，越大的话图像越胖，但是最高高度不变

所以，由这张图，思考一下，为什么这样可以表示多变量的分类器？

有3个点，越接近一个点，其对应的值越接近1 。越远离， 其对应的值越接近于 0-

这就是如何用核函数来实现复杂的非线性分类器!!

但是，仍有一些不懂的，其中一个是 我们如何得到这些标记点 我们怎么来选择这些标记点 另一个是 其他的相似度方程是什么样的 如果有其他的话 我们能够用其他的相似度方程 来代替我们所讲的这个高斯核函数吗

5. Kernels II 核函数进一步！

上节课回顾：

实际应用的时候，如何选择标记点？

只需要直接将训练样本当做标记点！

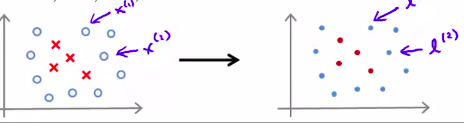
所以，下面是如何应用：

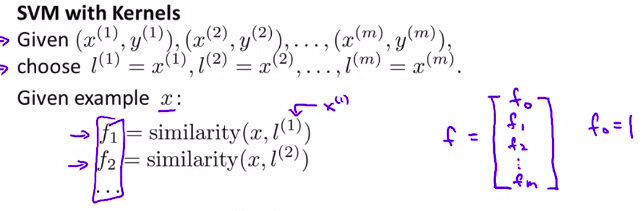
以上就是步骤。



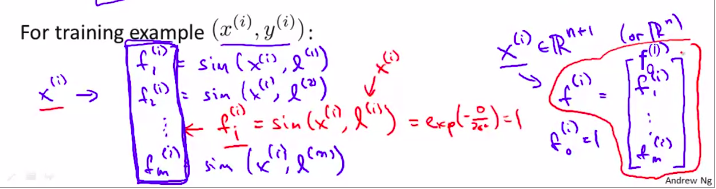
当然，这个f完全可以向量化。

如何具体操作？很简单！

只需要将hy函数替换一下

注：此时，仍然不用对 0 作正则化处理

正则项可以这样写：

一点的数学小细节

这样可以让支持向量机更高效的运行。因为这样可以适应超大量的训练集

再有一点，如何选择支持向量机中的参数？(2个参数)

如何进行方差和偏差折中？

总结的话，\(\delta\)变小，函数变化的越剧烈，导数越大。导致出现高方差，也就是over-fitting. 过拟合

变大的话，就是under-fitting欠拟合

6. 实际例子

一般计算参数\(\theta\)不需要自己写算法来实现，因为已经有高效实现的软件库。 但是，我们仍需要做一些事情：

例如：线性核函数，高斯核函数等等。

什么时候用线性分类器（线性核函数） ：

大量的特征量，训练集很少。

什么时候使用高斯核函数？

特征少，复杂，非线性

当使用matlab实现的时候：

用高斯核函数的时候，不同的特征量一定要记得归一化

因为不同的特征量的差距可能会非常大！！

注：其他的一些核函数kernals

---

最后讨论2个细节：

多分类问题

如何让SVM输出各个类别间合适的判定边界？

一，用内置函数，在软件库里

二，用一对多方法, one vs all

1. 用向量机还是逻辑回归？
   
   

   注意：逻辑回归和线性核函数十分相似，但是有不同的算法
   
   对于神经网络：