矩阵快速幂(入门) 学习笔记hdu1005, hdu1575， hdu1757

矩阵快速幂是基于普通的快速幂的一种扩展，如果不知道的快速幂的请参见http://www.cnblogs.com/Howe-Young/p/4097277.html。二进制这个东西太神奇了，好多优秀的算法都跟他有关系，这里所说的矩阵快速幂就是把原来普通快速幂的数换成了矩阵而已，只不过重载了一下运算符*就可以了，也就是矩阵的乘法，  当然也可以写成函数，标题中的这三个题都是关于矩阵快速幂的基础题。拿来练习练习熟悉矩阵快速幂，然后再做比较难点的，其实矩阵快速幂比较难的是构造矩阵。下面还是那题目直接说话：

hdu1575：

题目大意：求一个矩阵k此方之后主对角线上的元素之和对9973取模

这个题是矩阵快速幂的裸题，直接用就行了。下面是代码

 #include<iostream>
 #include <string.h>
 #include <stdio.h>
 #include <algorithm>
 
 using namespace std;
 const int N = ;
 const int mod = ;
 struct Matrix{
     int a[N][N];
 };
 int n;
 Matrix operator * (Matrix t1, Matrix t2)//重载运算符 *
 {
     Matrix c;
     memset(c.a, , sizeof(c.a));
     //矩阵乘法
     for (int k = ; k < n; k++)
     {
         for (int i = ; i < n; i++)
         {
             if (t1.a[i][k] <= )
                 continue;
             for (int j = ; j < n; j++)
             {
                 if (t2.a[k][j] <= )
                     continue;
                 c.a[i][j] = (c.a[i][j] + t1.a[i][k] * t2.a[k][j]) % mod;
             }
         }
     }
     return c;
 }
 //重载^运算符
 Matrix operator ^ (Matrix t, int k)
 {
     Matrix c;
     memset(c.a, , sizeof(c.a));
     //初始化矩阵c为单位阵
     for (int i = ; i < n; i++)
     {
         c.a[i][i] = ;
     }
     //这里用到快速幂
     for (; k; k >>= )
     {
         if (k & )
             c = c * t;
         t = t * t;
     }
     return c;
 }
 int main()
 {
     int T, k;
     cin >> T;
     while (T--)
     {
         cin >> n >> k;
         Matrix t1, t2;
         for (int i = ; i < n; i++)
         {
             for (int j = ; j < n; j++)
                 cin >> t1.a[i][j];
         }
         t2 = t1 ^ k;
         int res = ;
         for (int i = ; i < n; i++)
             res = (res + t2.a[i][i]) % mod;
         cout << res << endl;
     }
 
     return ;
 }

hdu1005：

题目大意：

f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

给你A， B和n让你求f(n)是多少

这个题就需要稍微构造一下矩阵了

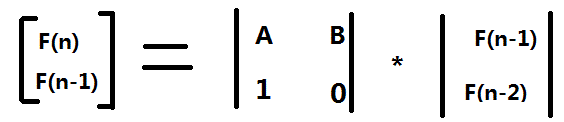
这样的话要求F(n)的话，只需要对求出来F(n-1)就行了，对应的F(n-1)要求出F(n-2)，所以题目给了F(1)和F(2)，所以乘以他前面的系数矩阵就为【F(3), F(2)】^T,再接着成系数矩阵就为【F(4)，F(3)】^T所以要求F(n)只需要对系数矩阵进行n-2次幂就行了，然后最后要求的结果就是矩阵的第一行第一列的结果，代码如下

 #include<iostream>
 #include <cstring>
 #include <cstdio>
 #include <algorithm>
 
 using namespace std;
 const int N = ;
 const int mod = ;
 struct Matrix
 {
     int mat[N][N];
 };
 //矩阵乘法(函数的形式)
 Matrix Multi(Matrix a, Matrix b)
 {
     Matrix c;
     memset(c.mat, , sizeof(c.mat));
     for (int i = ; i < N; i++)
     {
         for (int j = ; j < N; j++)
         {
             for (int k = ; k < N; k++)
                 c.mat[i][j] = (c.mat[i][j] + a.mat[i][k] * b.mat[k][j]) % mod;
         }
     }
     return c;
 }
 //矩阵快速幂 （函数形式）
 Matrix quickMatrixPower(Matrix a, int k)
 {
     Matrix t;
     memset(t.mat, , sizeof(t.mat));
     for (int i = ; i < N; i++)
         t.mat[i][i] = ;
     //快速幂
     while (k)
     {
         if (k & )
             t = Multi(t, a);
         a = Multi(a, a);
         k >>= ;
     }
     return t;
 }
 
 int main()
 {
     long long a, b, n;
     while (cin >> a >> b >> n && (a + b + n))
     {
         Matrix t;
         //初始化系数矩阵
         t.mat[][] = a;
         t.mat[][] = b;
         t.mat[][] = ;
         t.mat[][] = ;
         if (n >= )
         {
             t =  quickMatrixPower(t, n - );
             printf("%d\n", (t.mat[][] + t.mat[][]) % mod);
         }
         else
         {
             printf("%lld\n", n);
         }
     }
 
     return ;
 }

hdu1757

题目大意：

If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .

Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.

这个关键还是在于构造矩阵，因为给递推式了，所以矩阵还是比价好构造的，下图是构造的矩阵

推到过程类似于1005，不再赘述，代码如下：

 #include<iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 
 using namespace std;
 const int ori[][] = {, , , , , , , , , };
 struct Matrix
 {
     int str[][];
 };
 int m;
 //矩阵乘法
 Matrix operator * (Matrix a, Matrix b)
 {
     Matrix c;
     memset(c.str, , sizeof(c.str));
     for (int i = ; i < ; i++)
     {
         for (int j = ; j < ; j++)
         {
             for (int k = ; k < ; k++)
                 c.str[i][j] = (c.str[i][j] + a.str[i][k] * b.str[k][j]) % m;
        }
     }
     return c;
 }
 //矩阵快速幂
 Matrix power (Matrix a, int k)
 {
     Matrix c;
     memset(c.str, , sizeof(c.str));
     for (int i = ; i < ; i++)
         c.str[i][i] = ;
     while (k)
     {
         if (k & )
             c = c * a;
         a = a * a;
         k >>= ;
     }
     return c;
 }
 //最后一步的矩阵乘法
 int Multi(Matrix a)
 {
     Matrix c;
     memset(c.str, , sizeof(c.str));
     for (int i = ; i < ; i++)
     {
         for (int j = ; j < ; j++)
         {
             for (int k = ; k < ; k++)
             {
                 c.str[i][j] = (c.str[i][j] + ori[i][k] * a.str[k][j]) % m;
             }
         }
     }
     return c.str[][] % m;
 }
 int main()
 {
     int k;
     while (cin >> k >> m)
     {
         Matrix t;
         memset(t.str, , sizeof(t.str));
         for (int i = ; i < ; i++)
         {
             cin >> t.str[i][];
             for (int j = ; j < ; j++)
                 if (i +  == j)
                     t.str[i][j] = ;
         }
         if (k >= )
         {
             t = power(t, k - );
             printf("%d\n", Multi(t));
         }
         else
         {
             printf("%d\n", k);
         }
     }
 
     return ;
 }