POJ 1039 Pipe 枚举线段相交

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9493		Accepted: 2877

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting. 

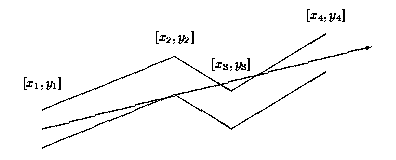
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find, for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent points and the bent points do not stop the light beam.

Input

The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted with n = 0.

Output

The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

Central Europe 1995

题目大意：给出一个管道，让一束光穿过，找出一个穿过距离最长的，然后求出这个穿过距离最长的与管壁的交点的x坐标，如果可以完整的穿过整个管道，输出Through all the pipe.

思路： 枚举光线是否可以穿过每一个拐点官腔，也就是拐点所在位置的竖直线段，如果不能穿过说明它肯定与管壁相交，计算交点，如果都能相交，这时就是可以穿过整个管道。

注：刚开始枚举的时候枚举的特别麻烦，是直接枚举光线方向，从入口一次加0.01的枚举，判断特殊位置的时候特别麻烦

/*************************************************************************
    > File Name:            poj_1039.cpp
    > Author:               Howe_Young
    > Mail:                 1013410795@qq.com
    > Created Time:         2015年05月01日 星期五 09时43分46秒
 ************************************************************************/
 
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#define EPS 1e-8
#define INF 1e6
using namespace std;
struct point{
    double x, y;
};
const int maxn = ;
point p[maxn];
int n;
int sgn(double x)
{
    if (fabs(x) < EPS)
        return ;
    return x <  ? - : ;
}
double x_multi(point p1, point p2, point p3)
{
    return (p3.x - p1.x) * (p2.y - p1.y) - (p2.x - p1.x) * (p3.y - p1.y);
}
void get_intersection(point p1, point p2, point p3, point p4, double &x, double &y)
{
    double a1, b1, c1, a2, b2, c2;//求交点过程
    a1 = (p2.y - p1.y) * 1.0;
    b1 = (p1.x - p2.x) * 1.0;
    c1 = (p2.x * p1.y - p1.x * p2.y) * 1.0;
    a2 = (p4.y - p3.y) * 1.0;
    b2 = (p3.x - p4.x) * 1.0;
    c2 = (p3.y * p4.x - p4.y * p3.x) * 1.0;
    x = (b1 * c2 - b2 * c1) / (b2 * a1 - b1 * a2);
    y = (a1 * c2 - c1 * a2) / (a2 * b1 - a1 * b2);
}
 
bool check(point p1, point p2, point p3, point p4)//p1p2是否穿过竖着的p3p4，查看这条线是否与每一个拐角处上下连接的线段都相交，包括端点
{
    double d1 = x_multi(p1, p2, p3);
    double d2 = x_multi(p1, p2, p4);
    return d1 * d2 <= ;
}
bool check2(point p1, point p2, point p3, point p4)//同理看p3, p4这两个点是否在p1p2两侧，端点不算
{
    double d1 = x_multi(p1, p2, p3);
    double d2 = x_multi(p1, p2, p4);
    return d1 * d2 < ;
}
point does(point p1)//它的对应的下一个端点
{
    p1.y--;
    return p1;
}
int main()
{
    while (~scanf("%d", &n) && n)
    {
        for (int i = ; i < n; i++)
        {
            scanf("%lf %lf", &p[i].x, &p[i].y);
        }
        point p0;
        double ans = p[].x;
        for (int i = ; i < n; i++)
        {
            for (int j = ; j < n; j++)
            {
                if (i == j)
                    continue;
                if (check(p[i], does(p[j]), p[], does(p[])))//如果光线可以从入口射进来
                {
                    for (int k = ; k < n; k++)
                    {
                        if (!check(p[i], does(p[j]), p[k], does(p[k])))//如果走到k点这个拐点与管壁相交了，找出相交的点来
                        {
                            if (check2(p[i], does(p[j]), p[k], p[k - ]))//如果与上壁相交
                            {
                                get_intersection(p[i], does(p[j]), p[k], p[k - ], p0.x, p0.y);
                                if (ans < p0.x)
                                    ans = p0.x;
                                break;
                            }
                            if (check2(p[i], does(p[j]), does(p[k]), does(p[k - ])))//如果与下壁相交
                            {
                                get_intersection(p[i], does(p[j]), does(p[k]), does(p[k - ]), p0.x, p0.y);
                                if (ans < p0.x)
                                    ans = p0.x;
                                break;
                            }//如果都不相交的话，那么说明是与上一段的端点相交
                            if (ans < p[k - ].x)
                                ans = p[k - ].x;
                            break;
                        }
                        if (k == n - )//如果走到最后都没break，也就是相交，那么说明可以通过这个管道，直接让他等于最后的x坐标
                        {
                            ans = p[n - ].x;
                        }
                    }
                }
            }
        }
        if (sgn(ans - p[n - ].x) == )
        {
            puts("Through all the pipe.");
        }
        else
            printf("%.2f\n", ans);
    }
    return ;
}