尼姆博弈+SG函数

博弈这个东西真的很费脑诶..

尼姆博奕（Nim Game）：游戏者轮流从一堆棋子（或者任何道具）中取走一个或者多个，最后不能再取的就是输家。当指定相应数量时，一堆这样的棋子称作一个尼姆堆

当n堆棋子的数量满足a1 xor a2 xor a3 xor.......xor an=0（Bouton's Theorem）时 为必败态，即先手必败（对于这种局面我们叫它奇异局面），对于尼姆博弈这种游戏，寻找必败态是非常重要的，那么对于必败态 有：

1.无法进行任何移动的自然是比败态

2.可以移动到必败态的是非必败态

3.必败态无论怎么操作都是非必败态，就是说如果自己处于必败态的话，无论怎么移动，都不可能赢（必败了嘛...迫真）。

对于a1 xor a2 xor a3 xor.......xor an=0做个解释：

1.对于（0，0，0)我们无法做出任何移动，先手必败，即0 xor 0 xor 0=0

2.如果对于某个局面（a1,a2,.....an),若a1 xor a2 xor a3 xor.......xor an=k（k≠0），那么k的二进制最高位的1必定来自于其中一个ai对应的的二进制位上的1，显然a1 xor k<=a1,那么只需要通过移动棋子将ai变为a1 xor k，那么等式变为a1 xor a2 xor a3 xor.......xor an xor k=k xor k=0,即可变为必败态

3.若处于某个局面（a1,a2.....an)，,若a1 xor a2 xor a3 xor.......xor an=0，如果我们将ai变为ai'，使得异或结果为0，但是由于异或满足消去律，那么对于a1 xor a2 xor a3....xor ai xor .....xor an=a1 xor a2 xor a3....xor ai' xor .....xor an,则说明ai=ai'，该移动不合法（根本没移动好伐)，与假设相矛盾

那么勉强证出来了。

对于取走棋子个数最多为m个的，只需将每堆棋子个数%（m+1)即可。

但是！如果问题突然蛇皮，比如有n堆石子，每次可以从第1堆石子里取1颗、2颗或3颗，可以从第2堆石子里取奇数颗，可以从第3堆及以后石子里取任意颗，那咋整啊，总不能电波求解吧

那肯定不是 这个时候SG(Sprague-Grundy)函数就开始发挥自己的作用了

定义P-position和N-position,分别表示先手必败的局面和后手必败的局面，p表示previous，n表示next，更严谨的定义是：1.无法进行任何移动的局面（也就是terminal position）是P-position；2.可以移动到P-position的局面是N-position；3.所有移动都导致N-position的局面是P-position。那么我们将这个游戏转化为图，给定一个有向无环图和一个起始点上的一个棋子，两个玩家分别在图上顺着有向边移动棋子，当无法移动时说明现在操作的玩家输了，我们可以将所有的组合游戏（Impartial Combinatorial Games），通过将每个局面看到一个顶点，每个局面和每个子局面以变换方式作为有向边相连，抽象成这个图模型，下面我们就在有向无环图的顶点上定义Sprague-Garundy函数。

首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

对于一个给定的有向无环图，定义关于图的每个顶点的SG函数g如下：g(x)=mex{ g(y) | y是x的后继 }。

来看一下SG函数的性质。首先，所有没有出边的顶点(terminal position所对应的顶点)，其SG值为0，因为它的后继集合是空集。然后对于一个g（x)=0的顶点x，它所有后继y都满足g（y)!=0。对于一个g(x)!=0的顶点，必定存在一个后继y满足g(y)=0。画个图大概会好懂一点。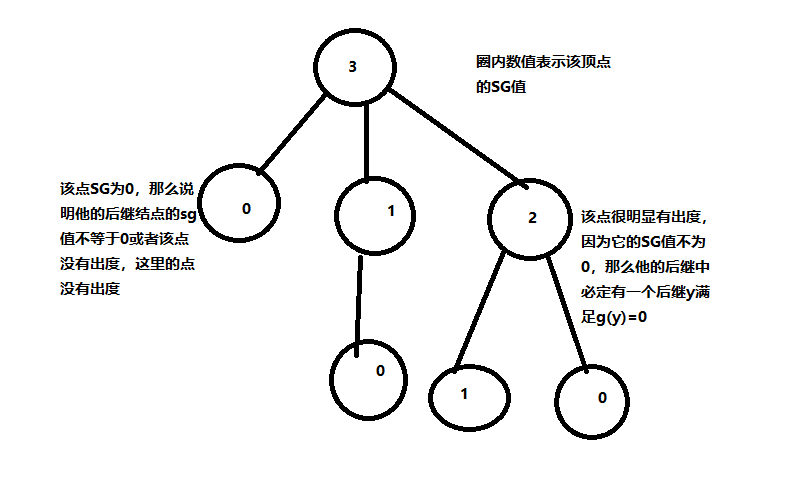

那么顶点x所代表的postion是P-position当且仅当g(x)=0（跟P-positioin/N-position的定义的那三句话是完全对应的）。如果我们的点从g(x)=0处出发，要么一开始我们就无路可走，就是输了，要么我们可以走到下面的g(y)!=0处，那么y的后继中必有z使得g(z)=0，当对手将棋子移动到这里时，我们要么无路可走，要么重复上面的步骤，最终总会无路可走，毕竟无环，那么即为先手必败。那么我们通过计算有向无环图的每个顶点的SG值，就可以对每种局面找到必胜策略了。但是SG函数的用途远没有这么简单。如果将这个有向图游戏变复杂一点，比如说，有向图上并不是只有一枚棋子，而是有n枚棋子，每次可以任意选一枚进行移动，那么这个时候我们又如何去找到必胜策略呢？

让我们再来考虑一下顶点的SG值的意义。当g(x)=k时，表明对于任意一个0<=i<k，都存在x的一个后继y满足g(y)=i。也就是说，当某枚棋子的SG值是k时，我们可以把它变成0、变成1、……、变成k-1，但绝对不能保持k不变。是不是感觉和Nim游戏很像？Nim游戏的规则就是：每次选择一堆数量为k的石子，可以把它变成0、变成1、……、变成k-1，但绝对不能保持k不变。这表明，如果将n枚棋子所在的顶点的SG值看作n堆相应数量的石子，那么这个Nim游戏的每个必胜策略都对应于原来这n枚棋子的必胜策略！

对于n个棋子，设它们对应的顶点的SG值分别为(a1,a2,...,an)，再设局面(a1,a2,...,an)时的Nim游戏的一种必胜策略是把ai变成k，那么原游戏的一种必胜策略就是把第i枚棋子移动到一个SG值为k的顶点。我们从Nim到SG，然后又从SG到了Nim,=- =这的确很神奇。

其实我们还是只要证明这种多棋子的有向图游戏的局面是P-position当且仅当所有棋子所在的位置的SG函数的异或为0。这个证明与上节的Bouton's Theorem几乎是完全相同的，只需要适当的改几个名词就行了。

刚才我们为了简化问题，将n枚棋子放在同一个有向图上移动，但如果是每个棋子在其对应的有向图上，每次任选一个棋子（就是任选一个有向图）进行移动，显然对结论也不会有什么影响。

所以我们可以定义有向图游戏的和(Sum of Graph Games)：设G1、G2、……、Gn是n个有向图游戏，定义游戏G是G1、G2、……、Gn的和(Sum)，游戏G的移动规则是：任选一个子游戏Gi并移动上面的棋子。Sprague-Grundy Theorem就是：g(G)=g(G1)^g(G2)^...^g(Gn)。也就是说，游戏的和的SG函数值是它的所有子游戏的SG函数值的异或。

再考虑之前说的：任何一个组合游戏（ICG）都可以抽象成一个有向图游戏。所以“SG函数”和“游戏的和”的概念就不是局限于有向图游戏。我们给每个ICG的每个position定义SG值，也可以定义n个ICG的和。所以说当我们面对由n个游戏组合成的一个游戏时，只需对于每个游戏找出求它的每个局面的SG值的方法，就可以把这些SG值全部看成Nim的石子堆，然后依照找Nim的必胜策略的方法来找这个游戏的必胜策略了！（Nim其实就是n个从一堆中拿石子的游戏求SG的变型，总SG=n个sg的异或）。

回到之前问题。有n堆石子，每次可以从第1堆石子里取1颗、2颗或3颗，可以从第2堆石子里取奇数颗，可以从第3堆及以后石子里取任意颗……我们可以把它看作3个子游戏，第1个子游戏只有一堆石子，每次可以取1、2、3颗，可以看出x颗式子的局面的SG值是x%4。(尽量自己画图试试）第2个子游戏也是只有一堆石子，每次可以取奇数颗，经过简单的画图可以知道这个游戏有x颗石子时的SG值是x%2。第3个游戏有n-2堆石子，就是一个Nim游戏。对于原游戏的每个局面，把三个子游戏的SG值异或一下就得到了整个游戏的SG值，然后就可以根据这个SG值判断是否有必胜策略以及做出决策了。其实看作3个子游戏还是保守了些，干脆看作n个子游戏，其中第1、2个子游戏如上所述，第3个及以后的子游戏都是“1堆石子，每次取几颗都可以”，称为“任取石子游戏”，这个超简单的游戏有x颗石子的SG值显然就是x。其实，n堆石子的Nim游戏本身不就是n个“任取石子游戏”的和吗？

所以，对于我们来说，SG函数与“游戏的和”的概念不是让我们去组合、制造稀奇古怪的游戏，而是把遇到的看上去有些复杂的游戏试图分成若干个子游戏，对于每个比原游戏简化很多的子游戏找出它的SG函数，然后全部异或起来就得到了原游戏的SG函数，就可以解决原游戏了。

解题模型：

1.把原游戏分解成多个独立的子游戏，则原游戏的SG函数值是它的所有子游戏的SG函数值的异或。

即sg(G)=sg(G1)^sg(G2)^...^sg(Gn)。

2.分别考虑没一个子游戏，计算其SG值。

SG值的计算方法：

1.可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);

2.可选步数为任意步，SG(x) = x;

3.可选步数为一系列不连续的数，用模板计算。（我比较倾向dfs..

模版1:打表

 /* 1.可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);
 2.可选步数为任意步，SG(x) = x;
 3.可选步数为一系列不连续的数，用GetSG计算 */
 //f[]：可以取走的石子个数,f[0]表示有几种取法
 //SG[]:0~n的SG函数值
 //vis[]:mex{}
 int f[], SG[MAXN], vis[MAXN];
 void Get_SG(int n)
 {
     memset(SG, , sizeof(SG)); //SG[0]必为0
     for (int i = ; i <= n; i++)
     {
         memset(vis, , sizeof(vis));
         for (int j = ; j <= f[]; j++)
         {
             if (i < f[j])
                 break;
             else
                 vis[SG[i - f[j]]] = ;
         }
         for (int j = ; j <= n; j++)
             if (!vis[j])
             {
                 SG[i] = j;
                 break;
             }
     }
 }

模版2：DFS

 //注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍
 //n是集合s的大小 S[i]是定义的特殊取法规则的数组
 int s[],sg[],n;
 int SG_dfs(int x)
 {
     int i;
     if(sg[x]!=-)
         return sg[x];
     bool vis[];
     memset(vis,,sizeof(vis));
     for(i=;i<n;i++)
     {
         if(x>=s[i])
         {
             SG_dfs(x-s[i]);
             vis[sg[x-s[i]]]=;
         }
     }
     int e;
     for(i=;;i++)
         if(!vis[i])
         {
             e=i;
             break;
         }
     return sg[x]=e;
 }

附上HDU-1538http://acm.hdu.edu.cn/showproblem.php?pid=1536

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned long long ull;
 #define INF 0x3f3f3f3f
 const ll MAXN = 1e4 + ;
 const ll MOD = 1e9 + ;
 const double pi = acos(-);
 /* 1.可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);
 2.可选步数为任意步，SG(x) = x;
 3.可选步数为一系列不连续的数，用GetSG计算 */
 //注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍
 //n是集合s的大小 S[i]是定义的特殊取法规则的数组
 int s[], sg[], n;
 int SG_dfs(int x)
 {
     int i;
     if (sg[x] != -)
         return sg[x];
     bool vis[];
     memset(vis, , sizeof(vis));
     for (i = ; i < n; i++)
     {
         if (x >= s[i])
         {
             SG_dfs(x - s[i]);
             vis[sg[x - s[i]]] = ;
         }
     }
     int e;
     for (i = ;; i++)
         if (!vis[i])
         {
             e = i;
             break;
         }
     return sg[x] = e;
 }
 int main()
 {
     int k;
     while (~scanf("%d", &k), k)
     {
         n=k;
         string str = "";
         for (int i = ; i < k; i++)
             scanf("%d", &s[i]);
         sort(s, s + k);
         int m;
         memset(sg, -, sizeof(sg));
         scanf("%d", &m);
         for (int i = ; i < m; i++)
         {
             int ans = ;
             int n;
             scanf("%d", &n);
             for (int j = ; j < n; j++)
             {
                 int c;
                 scanf("%d", &c);
                 ans ^= SG_dfs(c);
             }
             if (ans)
                 str += "W";
             else
                 str += "L";
         }
         cout << str << endl;
     }
     return ;
 }