@hdu - 5960@ Subsequence

目录

• @description@
• @solution@
• @accepted code@
• @details@

---

@description@

给定如下计算序列权值的函数：



对于一个由三元组 (cost0, cost1, color) 组成的序列 A，求通过以上函数计算出来的第 k 大的子序列的权值。

Input

第一行一个整数 t，表示数据组数。

对于每组数据，第一行包含两个整数 n, k。

接下来 n 行，每行三个整数 cost0, cost1, color (0 <= cost0, cost1<= 10000；0 <=color <=1)，第 i 行描述 A 的第 i 个三元组。

保证至少有 k 个非空子序列。单组数据中 n <= 50000。∑n <= 400000，∑k <= 400000。

Output

对于每一行，输出对应的答案。

Sample Input

1

3 4

2 1 0

1 3 1

3 1 1

Sample Output

3

Hint

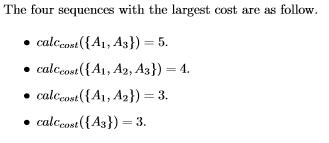
@solution@

大多数的 k 大问题都可以对应转化成 k 短路的模型，只是有些只能用 k 短路的思想来做而不能直接写裸 k 短路。

k 短路怎么做呢？在技术不发达的时代可以用 A* 玄学搜索，但现在发达了，于是我们有了效率更高的做法。

假如我们要求 s 到 t 的 k 短路，我们可以先求出在反向图中以 t 为根的最短路树（即每个点到 t 的最短路径构成的树）。

于是这样，s 到 t 的每一条路径将会经过一些树边与非树边。我们不妨用路径经过的非树边序列表示这样一条路径。

接下来，我们用优先队列存储当前的非树边序列。每一次选出最小的序列并进行拓展。

对于一个非树边序列，每一次拓展，要么在序列最末加入一条非树边，要么替换掉序列最后的非树边。

那么拓展 k 次后就可以得到我们的 k 短路。

最短路肯定就是 s 到 t 的纯树边道路（即非树边序列为空），我们将其加入初始优先队列。

怎么实现呢？我们先对于每条非树边 u -> v : w 算出 -dis[u] + w + dis[v]，即选择这条非树边会增加的代价，记为它的权值。

然后用可持久化可并堆，得到 x 到 t 的树边路径上所有点连出去的非树边构成的堆。

于是在最末加入一条新的非树边就很好操作了：取出最末非树边 (u, v) 的 v 对应的那个堆的堆顶。

那么怎么进行替换呢？我们在每个优先队列的结点中再存储一个可持久化可并堆，表示可用决策。

每次进行替换时，将可并堆的堆顶删除得到新的可用决策。

OK。我们来看这道题怎么转成 k 短路。

其实很简单，我们建 2*(n+2) 个点，第 i 对点表示 cur = 0 与 cur = 1 两种状态。

其中第 0 对（中 cur = 0 的那个点）表示源点，第 n + 1 对表示汇点。

然后对应在 i-1 与 i 之间连一连就好啦。

@accepted code@

#include<queue>
#include<vector>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define fi first
#define se second
#define mp make_pair
#define rep(G, x) for(Graph::edge *p = G.adj[x];p;p = p->nxt)
typedef pair<int, int> pii;
typedef long long ll;
const int MAXN = 50000;
struct Heap{
    struct node{
        node *ch[2];
        int dis, key, num;
    }pl[100*MAXN + 5], *ncnt, *NIL;
    Heap() {
        NIL = &pl[0];
        NIL->ch[0] = NIL->ch[1] = NIL;
        NIL->key = NIL->dis = 0;
    }
    node *newnode(int k, int p) {
        ncnt++;
        ncnt->ch[0] = ncnt->ch[1] = NIL;
        ncnt->key = k, ncnt->num = p, ncnt->dis = 1;
        return ncnt;
    }
    node *newnode(node *x) {
        ncnt++; *ncnt = *x;
        return ncnt;
    }
    void pushup(node *x) {
        if( x->ch[1]->dis > x->ch[0]->dis )
            swap(x->ch[0], x->ch[1]);
        x->dis = x->ch[1]->dis + 1;
    }
    node *merge(node *x, node *y) {
        if( x == NIL ) return y;
        if( y == NIL ) return x;
        if( x->key < y->key ) swap(x, y);
        node *p = newnode(x);
        p->ch[1] = merge(x->ch[1], y);
        pushup(p); return p;
    }
    void clear() {ncnt = &pl[0];}
    node *insert(node *x, int k, int p) {return merge(x, newnode(k, p));}
    node *erase(node *x) {return merge(x->ch[0], x->ch[1]);}
}T;
struct node{
    int x, k, dis; Heap::node *rt;
    node(int _x=0, int _k=0, int _d=0, Heap::node *_rt=T.NIL):x(_x), k(_k), dis(_d), rt(_rt) {}
    friend bool operator < (const node a, const node b) {
        return a.dis < b.dis;
    }
};
struct Graph{
    struct edge{
        int to, dis, id;
        edge *nxt;
    }edges[4*MAXN + 5], *adj[2*MAXN + 5], *ecnt;
    void addedge(int u, int v, int w, int id) {
        edge *p = (++ecnt);
        p->to = v, p->dis = w, p->id = id;
        p->nxt = adj[u], adj[u] = p;
    }
    void clear(int n) {
        for(int i=1;i<=n;i++) adj[i] = NULL;
        ecnt = &edges[0];
    }
}G1, G2;
int ecnt;
void addedge(int u, int v, int w) {
    ecnt++, G1.addedge(u, v, w, ecnt), G2.addedge(v, u, w, ecnt);
}
Heap::node *rt[2*MAXN + 5];
int pre[2*MAXN + 5], dis[2*MAXN + 5], ind[2*MAXN + 5];
void topo(int s, int t) {
    for(int i=s;i<=t;i++)
        rep(G2, i) ind[p->to]++;
    queue<int>que;
    for(int i=s;i<=t;i++) {
        if( ind[i] == 0 ) que.push(i);
        pre[i] = dis[i] = -1;
    }
    dis[t] = 0, rt[t] = T.NIL;
    while( !que.empty() ) {
        int f = que.front(); que.pop();
        rep(G2, f) {
            int t = p->to, id = p->id;
            if( dis[f] + p->dis > dis[t] ) {
                dis[t] = dis[f] + p->dis;
                pre[t] = id;
            }
            ind[t]--;
            if( ind[t] == 0 ) {
                rt[t] = T.NIL;
                rep(G1, t) {
                    if( p->id == pre[t] )
                        rt[t] = T.merge(rt[t], rt[p->to]);
                    else rt[t] = T.insert(rt[t], dis[p->to] - dis[t] + p->dis, p->to);
                }
                que.push(t);
            }
        }
    }
}
int get_kth(int s, int t, int k) {
    topo(s, t);
    priority_queue<node>que;
    que.push(node(s, dis[s], dis[s], T.NIL));
    for(int i=1;i<=k;i++) {
        node t = que.top(); que.pop();
        if( i == k ) return t.dis;
        if( t.rt != T.NIL )
            que.push(node(t.rt->num, t.k, t.k + t.rt->key, T.erase(t.rt)));
        if( rt[t.x] != T.NIL )
            que.push(node(rt[t.x]->num, t.dis, t.dis + rt[t.x]->key, T.erase(rt[t.x])));
    }
    return -1;
}
int cost[2][MAXN + 5], clr[MAXN + 5], id[2][MAXN + 5];
void solve() {
    T.clear(); int n, k, cnt = 0;
    scanf("%d%d", &n, &k);
    for(int i=0;i<=n;i++)
        id[0][i] = (++cnt), id[1][i] = (++cnt);
    int s = id[0][0], t = ++cnt;
    G1.clear(t), G2.clear(t), ecnt = 0;
    for(int i=1;i<=n;i++) {
        scanf("%d%d%d", &cost[0][i], &cost[1][i], &clr[i]);
        for(int j=0;j<2;j++)
            addedge(id[j][i-1], id[j][i], 0), addedge(id[j][i-1], id[clr[i]][i], cost[j][i]);
    }
    addedge(id[0][n], t, 0), addedge(id[1][n], t, 0);
    printf("%d\n", get_kth(s, t, k));
}
int main() {
    int T; scanf("%d", &T);
    while( T-- ) solve();
}

@details@

我一开始写的是带标记的可持久化堆（也就是没有建图跑 k 短路这么简单粗暴的方法）：维护两个堆 A, B 分别表示 cur = 0 与 cur = 1 的情况，每次要么往 A, B 中插入元素，要么 A, B 同时加上一个权值。

然后就被卡空间了。可喜可贺，可喜可贺。