js算法之寻路

A*寻路算法

算法流程说明：

说明：起始节点记作S，目标节点记作E，对于任意节点P，从S到当前节点P的总移动消耗记作GP，节点P到目标E的曼哈顿距离记作HP，从节点P到相邻节点N的移动消耗记作DPN，用于优先级排序的值F(N)记作FP

1. 选择起始节点S和目标节点E，将(S,0)（节点，节点F(N)值）放入openList，openList是一个优先队列，节点F(N)值越小，优先级越高。
2. 判断openList是否为空，若为空，则搜索失败，目标节点不可达；否则，取出openList中优先级最高的节点P;
3. 遍历P的上下左右四个相邻接点N1-N4，对每个节点N，如果N已经在closeList中，忽略；否则有两种情况;
   • 如果N不在openList中，令GN=GP+DPN，计算N到E的曼哈顿距离HN，令FN=GN+HN，令N的父节点为P，将(N,FN)放入openList；
   • 如果N已经在openList中，计算GN1= GP+DPN，如果GN1小于GN，那么用新的GN1替换GN，重新计算FN，用新的(N,FN)替换openList中旧的(N,FN)，令N的父节点为P；如果GN1不小于GN，不作处理。
4. 将节点P放入closeList中。判断节点P是不是目标节点E，如果是，搜索成功，获取节点P的父节点，并递归这一过程（继续获得父节点的父节点），直至找到初始节点S，从而获得从P到S的一条路径；否则，重复步骤2;

效果如下：

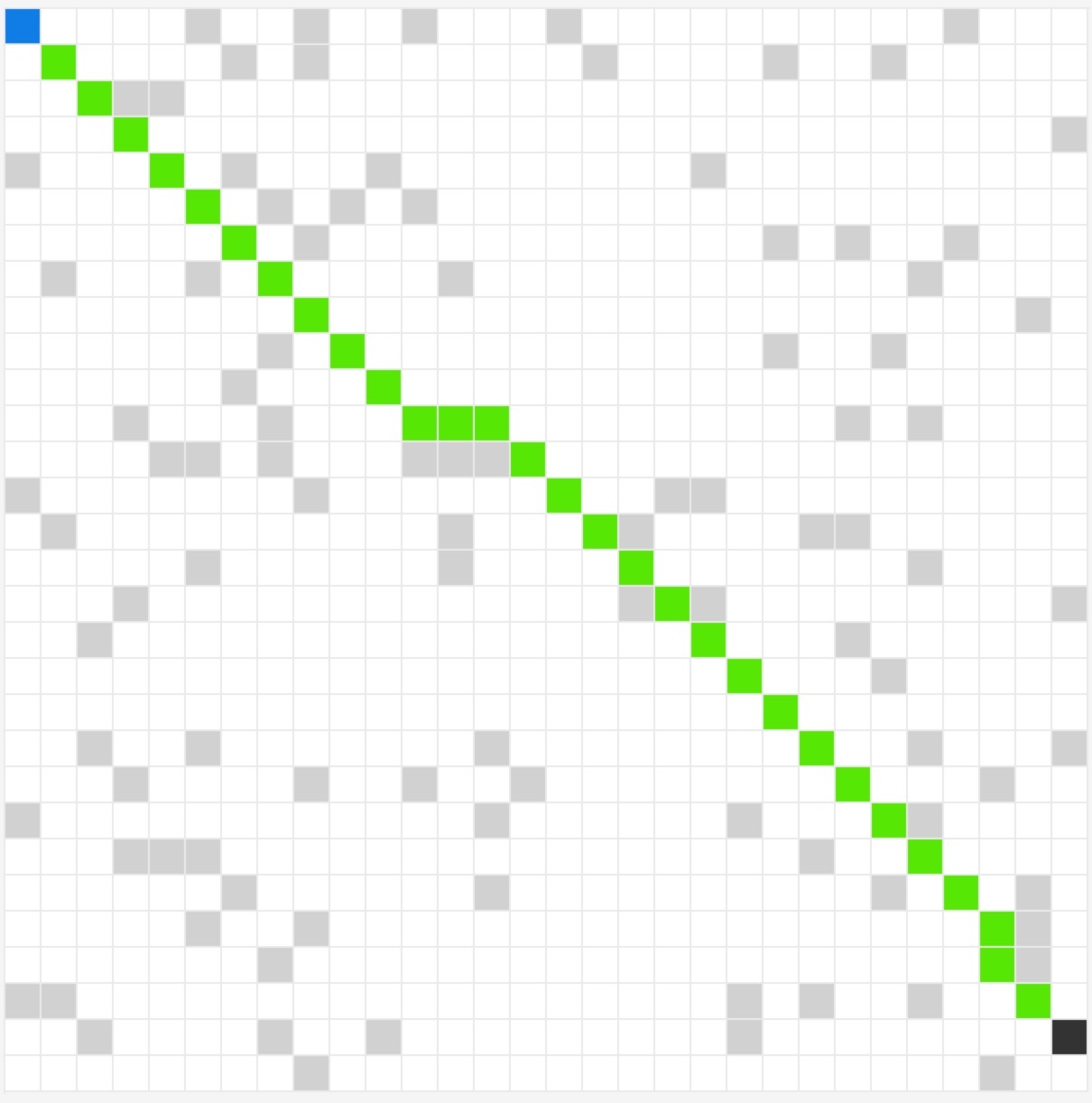
主要代码

// 寻路
function findWay(mapArr, oStart, oEnd) {
    let curPoint = null,
        bFind = true;  // 是否检索
    curPointArr = [];  // 当前指针
    let n = 0;

    let startX = oStart.x,
        startY = oStart.y,
        endX = oEnd.x,
        endY = oEnd.y;
    curPoint = oStart;
    //起始和结束相邻，直接结束
    if ((Math.abs(startX - endY) == 1 && Math.abs(startY - endY) == 1) || (Math.abs(startX - endX) == 0 && Math.abs(startY - endY) == 1) || (Math.abs(startX - endX) == 1 && Math.abs(startY - endY) == 0)) {
        bFind = false;
        setTimeout(function () {
            alert('起始和结束位置相邻');
        }, 300)
    }

    // 递归寻路
    while (bFind) {
        opens = getRound(curPoint);
        if (opens.length == 0) {
            alert('无路可走');
            return;
        }
        // 选取最近的路线
        opens.sort(function (a, b) {
            return a.num - b.num;
        });
        curPoint = opens.shift();
        curPointArr.push(curPoint);
        // 关闭其他路线
        closes = closes.concat(opens);
        closes.push(curPoint);
        opens = [];
        // 结束
        if (curPoint == oEnd) {
            bFind = false;
        }
    }
    if (!bFind) {
        showLine()
    }
}

// 获取打开的opensList
function getRound(curPoint) {
    let opens = [];
    let curX=curPoint.x,
        curY=curPoint.y;
    for (let i = 0; i < mapArr.length; i++) {
        for (let j = 0; j < mapArr[0].length; j++) {
            // 选取可以走的可能
            //走斜线
            if ((Math.abs(curX - i) == 0 && Math.abs(curY - j) == 1) || (Math.abs(curX - i) == 1 && Math.abs(curY - j) == 0) || (Math.abs(curX - i) == 1 && Math.abs(curY - j) == 1)) {
                if (closes.indexOf(mapArr[i][j]) == -1 && mapArr[i][j].val != 3 && mapArr[i][j] != oStart) {
                    if (curX<mapArr.length-1 && mapArr[curX + 1][curY].val == 3) {
                        if (j<mapArr[0].length-1 && mapArr[curX][curY+1].val == 3 && curX + 1 == i && curY + 1 == j) {
                            continue;
                        }else if(curY>0 && mapArr[curX][curY-1].val==3 && curX + 1 == i && curY - 1 == j) {
                            continue;
                        }
                    }else if (curX>0 && mapArr[curX - 1][curY].val == 3) {
                        if (curY<mapArr[0].length-1 && mapArr[curX][curY+1].val == 3 && curX - 1 == i && curY + 1 == j) {
                            continue;
                        }else if(curY>0 && mapArr[curX][curY-1].val==3 && curX - 1 == i && curY - 1 == j) {
                            continue;
                        }
                    }
                    mapArr[i][j].num = h(mapArr[i][j]);
                    opens.push(mapArr[i][j]);
                }
            }
        }
    }
    return opens
}

源代码下载：https://github.com/LianJianQiang/algorithm.git

参考文章：

JS算法之A*寻路