Johnson–Lindenstrauss 定理-Johnson–Lindenstrauss lemma
Johnson–Lindenstrauss 定理是这样的:一个一百万维空间里的随便一万个点,一定可以几乎被装进一个几十维的子空间里!
严格说来是这样:在 M 维空间中的 N 个点,几乎总是被包含在一个 D 维子空间里的。这里的 D 按照直觉应当等于 N 的阶,可是实际上我们只需要让 D 是 log(N) 的阶就可以了。这里「几乎被包含在」的确切含义是它在这个子空间上的投影几乎是等距的(允许有一个 ε 的误差,而常数 D/log(N) 就依赖于 ε)。很显然,这件事情在高维数据降维时有极重要的意义。
这个定理的证明很初等。它依赖于这样的一个基本概率事实:一个随机的 M 维单位向量到一个随机的 D 维子空间上的投影的长度几乎一定约等于 D/M。这件事情本身也有点不同寻常,虽然它可以通过简单的计算来证实。这是概率论计算中常常出现的由于高维度而导致的反直觉现象的一例。
这让我想起另一个高维度导致的悖论,是我在学大数定律时了解到的。在 M 维单位立方体中随机取一个点,当 M 充分大时根据大数定理容易算出这个点到立方体中心的距离几乎一定等于 √(M/3)/2。于是这就说明 M 维实心单位立方体几乎就完全位于一个半径为 √(M/3)/2 的球壳上。这里没有任何捣鬼之处,事实上就是如此。
Johnson–Lindenstrauss 引理表明任何高维数据集均可以被随机投影到一个较低维度的欧氏空间,同时可以控制pairwise距离的失真.
理论边界
由一个随机投影P所引入的失真是确定的,这是由于p定义了一个esp-embedding.其概率论定义如下:

u和v是从一个形状是[n样例,n特征]=[n_samples, n_features]的数据集中的任意行,p室友一个形状是[n成分,n特征]=[n_components, n_features]的随机高斯N(0,1)矩阵的投影(或一个稀疏Achlioptas矩阵).
用于保证eps-embedding的最小成分数有下面的公式得到:
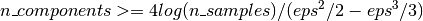
Johnson–Lindenstrauss 定理-Johnson–Lindenstrauss lemma的更多相关文章
- 最短路径算法——Dijkstra,Bellman-Ford,Floyd-Warshall,Johnson
根据DSqiu的blog整理出来 :http://dsqiu.iteye.com/blog/1689163 PS:模板是自己写的,如有错误欢迎指出~ 本文内容框架: §1 Dijkstra算法 §2 ...
- Latex中定义、定理、引理、证明 设置方法总结
Latex中定义.定理.引理.证明 设置方法总结 在LaTex中需要有关定理.公理.命题.引理.定义等时,常用如下命令 \newtheorem{定理环境名}{标题}[主计数器名] \newtheore ...
- Theorem、Proposition、Lemma和Corollary等的解释与区别
Theorem:定理.是文章中重要的数学化的论述,一般有严格的数学证明. Proposition:可以翻译为命题,经过证明且interesting,但没有Theorem重要,比较常用. Lemma:一 ...
- [未完成]scikit-learn一般实例之九:用于随机投影嵌入的Johnson–Lindenstrauss lemma边界
Johnson–Lindenstrauss 引理表明任何高维数据集均可以被随机投影到一个较低维度的欧氏空间,同时可以控制pairwise距离的失真. 理论边界 由一个随机投影P所引入的失真是确定的,这 ...
- 基于Hash算法的高维数据的最近邻检索
一.摘要 最紧邻检索:一种树基于树结构,一种是基于hash a.随机投影算法,需要产生很多哈希表,才能提高性能. b.基于学习的哈希算法在哈希编码较短时候性能不错,但是增加编码长度并不能显著提高性能. ...
- NLP相关问题中文本数据特征表达初探
1. NLP问题简介 0x1:NLP问题都包括哪些内涵 人们对真实世界的感知被成为感知世界,而人们用语言表达出自己的感知视为文本数据.那么反过来,NLP,或者更精确地表达为文本挖掘,则是从文本数据出发 ...
- NLP问题特征表达基础 - 语言模型(Language Model)发展演化历程讨论
1. NLP问题简介 0x1:NLP问题都包括哪些内涵 人们对真实世界的感知被成为感知世界,而人们用语言表达出自己的感知视为文本数据.那么反过来,NLP,或者更精确地表达为文本挖掘,则是从文本数据出发 ...
- Java牛人
Java领域有很多著名的人物,他们为Java社区编写框架.产品.工具或撰写书籍改变了Java编程的方式.本文是<最受欢迎的8位Java牛人>的2.0版本. PS:排名不分先后.本文的信息整 ...
- Address Book(地址薄)
<?xml version="1.0" encoding="UTF-8"?> <?import javafx.scene.Scene?> ...
随机推荐
- 3. Vim入门教程
1. 基本概念 1.1 了解Vim的三个基本模式 当我们安装完一个编辑器后,肯定会打开它,然后在里面输入点什么东西,但是打你打开Vim后,想要输入点什么却发现自己什么都没有输入,所以在写点东西之前,先 ...
- 剑指offer——26反转链表
题目描述 输入一个链表,反转链表后,输出新链表的表头. 题解: 每次只反转一个节点,先记住cur->next, 然后pre->cur,即可; class Solution { pu ...
- 尾插法-实现链表反转(有点bug,以后再来研究下)
def func2(head): p = head.next while p.next: q = p.next p.next = q.next # 重点 head.next = q q.next = ...
- 《DSP using MATLAB》Problem 8.46
下雨了,大风降温,一地树叶,终于进入冬季了 代码: %% ----------------------------------------------------------------------- ...
- Win7+Ubuntu11.10(EasyBCD硬盘安装)----转载
Win7+Ubuntu11.10(EasyBCD硬盘安装) ubuntu 下载地址:http://mirrors.163.com/ubuntu-releases/12.04/ 1)首先还是分区,在计算 ...
- eclipse导入别人项目配置tomcat和jdk
1.file--import--General--Existing Projiect into Workspace-- 2.导入项目成功后,项目会有错误,需重新进行tomcat及jdk的配置 项目名右 ...
- Python中and_Or
自 http://www.cnblogs.com/BeginMan/p/3197123.html 一.and: 在Python 中,and 和 or 执行布尔逻辑演算,如你所期待的一样,但是它们并不返 ...
- MD5/SHA1/Hmac_SHA1
1.MD5 #import <CommonCrypto/CommonDigest.h> + (NSString *) md5:(NSString *) input { const char ...
- windows下怎么给ubantu虚拟机全屏的处理
ubantu版本时16.04 windows下窗口太小需要设置 相信很多人在装虚拟机的时候,遇到了窗口过小不能自适应的问题.我也是查了好多资料,都说安装Vmware Tools即可解决,还有说修改分辨 ...
- laravel sql mode only_full_group_by 解决小记
環境: mysql: 5.7.* Laravel: 5.4.* sql 中使用到了 group by,會提示 500錯誤,將 config/database.php中的 strict的值改爲true, ...
