poj 1085 Triangle War （状压+记忆化搜索）

Triangle War

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2685		Accepted: 1061

Description

Triangle War is a two-player game played on the following triangular grid: 


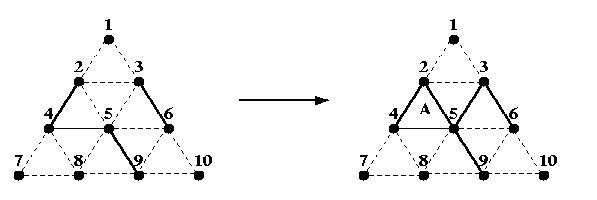
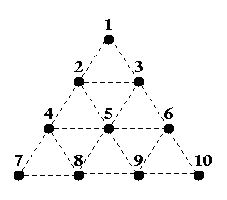Two players, A and B, take turns filling in any dotted line connecting two dots, with A starting first. Once a line is filled, it cannot be filled again. If the line filled by a player completes one or more triangles, she owns the completed triangles and she
is awarded another turn (i.e. the opponent skips a turn). The game ends after all dotted lines are filled in, and the player with the most triangles wins the game. The difference in the number of triangles owned by the two players is not important. 

For example, if A fills in the line between 2 and 5 in the partial game on the left below: 


Then, she owns the triangle labelled A and takes another turn to fill in the line between 3 and 5. B can now own 3 triangles (if he wishes) by filling in the line between 2 and 3, then the one between 5 and 6, and finally the one between 6 and 9. B would then
make one more move before it is A's turn again. 
In this problem, you are given a number of moves that have already been made. From the partial game, you should determine which player will win assuming that each player plays a perfect game from that point on. That is, assume that each player always chooses
the play that leads to the best possible outcome for himself/herself.

Input

You will be given a number of games in the input. The first line of input is a positive integer indicating the number of games to follow. Each game starts with an integer 6 <= m <= 18 indicating the number of moves that have been made in the game. The next
m lines indicate the moves made by the two players in order, each of the form i j (with i < j) indicating that the line between i and j is filled in that move. You may assume that all given moves are legal.

Output

For each game, print the game number and the result on one line as shown below. If A wins, print the sentence "A wins." If B wins, print "B wins."

Sample Input

4
6
2 4
4 5
5 9
3 6
2 5
3 5
7
2 4
4 5
5 9
3 6
2 5
3 5
7 8
6
1 2
2 3
1 3
2 4
2 5
4 5
10
1 2
2 5
3 6
5 8
4 7
6 10
2 4
4 5
4 8
7 8 

Sample Output

Game 1: B wins.
Game 2: A wins.
Game 3: A wins.
Game 4: B wins.

Source

field=source&key=East+Central+North+America+1999" rel="nofollow" style="text-decoration:none;">East Central North America 1999

题意：

两个人玩游戏，依次在三角形上放边，假设能构成三角形。则奖励继续该此人放，问最后得到的三角形多。

思路：

给边编号，记忆化搜索即可。做过好多这样的题。就不多写思路了。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#pragma comment (linker,"/STACK:102400000,102400000")
#define maxn 1005
#define MAXN 50005
#define mod 1000000009
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-6
typedef long long ll;
using namespace std;

int n,m,ans,cnt,tot,flag;
bool vis[10];
int dp[300000],mp[15][15],sc[5];
int tri[9][3]=
{
    0,1,2,3,4,7,2,4,5,5,6,8,9,10,15,
    7,10,11,11,12,16,8,12,13,13,14,17
};

int cal(int s)
{
    int i,j,t=0;
    for(j=0; j<9; j++)
    {
        if((s&(1<<tri[j][0]))&&(s&(1<<tri[j][1]))&&(s&(1<<tri[j][2]))) t++;
    }
    return t;
}
int dfs(int state,int score)
{
    if(dp[state]!=-1) return dp[state];
    int i,j,t,tst,num,best=0,tmp;
    num=9-score;
    for(i=0; i<=17; i++)
    {
        if(state&(1<<i)) continue ;
        tst=state|(1<<i);
        t=cal(tst);
        if(t>num)
        {
            tmp=t-num+dfs(tst,score-(t-num));
            best=max(best,tmp);
        }
        else
        {
            tmp=score-dfs(tst,score);
            best=max(best,tmp);
        }
    }
    dp[state]=best;
    return best;
}
int main()
{
    int i,j,t,test=0;
    mp[1][2]=0;mp[1][3]=1;mp[2][3]=2;mp[2][4]=3;mp[2][5]=4;mp[3][5]=5;
    mp[3][6]=6;mp[4][5]=7;mp[5][6]=8;mp[4][7]=9;mp[4][8]=10;mp[5][8]=11;
    mp[5][9]=12;mp[6][9]=13;mp[6][10]=14;mp[7][8]=15;mp[8][9]=16;mp[9][10]=17;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        tot=0;
        int x,y,z,turn=0,num=0;
        sc[0]=sc[1]=0;
        memset(vis,0,sizeof(vis));
        for(i=1; i<=n; i++)
        {
            scanf("%d%d",&x,&y);
            z=mp[x][y];
            tot|=(1<<z);
            flag=0;
            for(j=0; j<9; j++)
            {
                if(vis[j]) continue ;
                if((tot&(1<<tri[j][0]))&&(tot&(1<<tri[j][1]))&&(tot&(1<<tri[j][2])))
                {
                    vis[j]=1;
                    num++;
                    flag=1;
                    sc[turn]++;
                }
            }
            if(!flag) turn^=1;
        }
        memset(dp,-1,sizeof(dp));
        z=dfs(tot,9-num);
        sc[turn]+=z;
        sc[turn^1]+=(9-num-z);
        if(sc[0]>sc[1]) printf("Game %d: A wins.\n",++test);
        else printf("Game %d: B wins.\n",++test);
    }
    return 0;
}