AcWing 213. 古代猪文 数学知识

传送门

题目描述：

给定整数n,q，计算 $q^{\sum_{d|n} C_{n}^{d}}$ mod 999911659。

输入格式

输入包括一行，包含两个整数n，q，用一个空格隔开。

输出格式

输出包括一行，包含一个整数表示最终结果。

数据范围

1≤n,q≤10⁹

输入样例：

4 2

输出样例：

2048

提示:对于n的每一个正因数d，都有一个的值，将它们全部加起来得到的和就是。

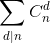题解：经典题，用到的数学知识比较多。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 4e4 + ;
const ll mod = ;
ll fac[N] = {},n,q,b[];
int a[] = {,,,,};
ll qp(ll a,ll b) {
    ll ans = ;
    for (;b;b>>=,a=a*a%mod)
        if (b&) ans = ans * a %mod;
    return ans;
}
void exgcd(ll a,ll b,ll &x,ll &y) {
    if (b == ) {
        x = ;
        y = ;
        return ;
    }
    exgcd(b,a%b,y,x);
    y -= (a/b)*x;
}
ll getinv(ll a,ll b) {
    ll x,y;
    exgcd(a,b,x,y);
    return (x%b+b)%b;
}
ll lucas(ll x,ll p) {
    ll ans = ;
    for (ll y = n;x;x/=p,y/=p) {
        ll a = x%p, b = y%p;
        ans = ans*fac[b]%p*getinv(fac[a],p)%p*getinv(b<a?:fac[b-a],p)%p;
    }
    return ans;
}
int main(){
    scanf("%lld%lld",&n,&q);
    q%=mod;
    if(!q) {
        printf("0\n");
        return ;
    }
    ll mod1 = mod -,ans = ,x,y;
    for (ll i = ; i <= ; i++) fac[i] = fac[i-]*i%mod1;
    for (ll i = ; i*i<=n; i++)
        if (n%i==) {
            for (int j = ; j <= ; j++)
                b[j] = (b[j]+lucas(i,a[j]))%a[j];
            if (i*i!=n) for (int j = ; j <= ; j++)
                b[j] = (b[j]+lucas(n/i,a[j]))%a[j];
        }
    for (int i = ; i <= ; i++){
        exgcd(mod1/a[i],a[i],x,y);
        ans = (ans+x*(mod1/a[i])%mod*b[i])%mod1;
    }
    ans = (ans+mod1)%mod1;
    ans = qp(q,ans);
    printf("%lld\n", ans);
    return ;
}