NOIP 华容道

描述

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

1. 在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；

2. 有些棋子是固定的，有些棋子则是可以移动的；

3. 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。 游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 EX_iEX​i​​ 行第 EY_iEY​i​​ 列，指定的可移动棋子的初始位置为第 SX_iSX​i​​ 行第 SY_iSY​i​​ 列，目标位置为第 TX_iTX​i​​ 行第 TY_iTY​i​​ 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

格式

输入格式

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。

接下来的 q 行，每行包含 6 个整数依次是 EX_iEX​i​​、EY_iEY​i​​、SX_iSX​i​​、SY_iSY​i​​、TX_iTX​i​​、TY_iTY​i​​，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

样例1

样例输入1

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

Copy

样例输出1

2
-1

Copy

限制

每个测试点1s。

提示

###样例说明

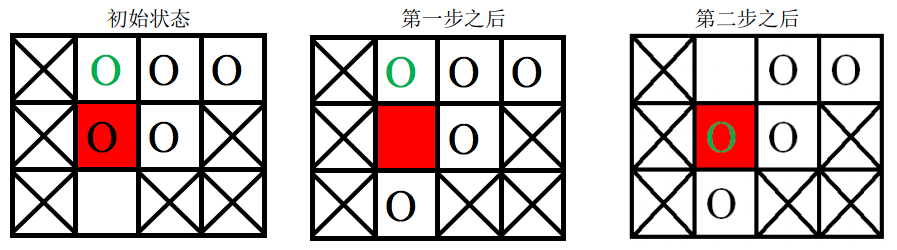
棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

1. 第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

   移动过程如下:

   

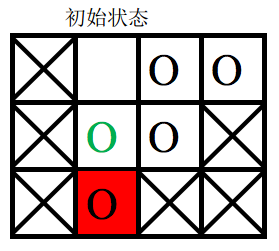
2. 第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

   

   要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2，2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。

###数据范围

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1； 
对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10； 
对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

来源

NOIP 2013 提高组 day 2

---

　　首先可以考虑全盘爆搜，让空白方块到处乱跑，状态要记录空白方块的位置和目标棋子的位置，所以状态总数为n²m²,时间复杂度为O(n²m²q).

　　然后来想想优化，当空白方块跑到目标棋子周围时，再到处瞎跑没什么意义而且多个询问棋盘不会改变，所以呢，可以考虑预处理一下当目标棋子的位置为(i, j)时，空白方块在目标棋子a方向时移到b方向最少要的步数。花费一个O(n²m²)的时间去跑nm次bfs。

　　这有什么用呢？我们先把空白棋子移到目标棋子周围然后就可以跑spfa了，spfa除了记录目标棋子的位置再记录一下空白棋子在哪个方向，转移的时候方向相反，这个距离就可以用之前预处理的结果了。这样总时间复杂度为O(n²m² + qn² + kqn²)，其中k为spfa的常数。

Code

 #include<iostream>
 #include<fstream>
 #include<sstream>
 #include<string>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<ctime>
 #include<cmath>
 #include<algorithm>
 #include<cctype>
 #include<vector>
 #include<stack>
 #include<set>
 #include<map>
 #include<queue>
 #ifndef WIN32
 #define Auto "%lld"
 #else
 #define Auto "%I64d"
 #endif
 using namespace std;
 typedef bool boolean;
 #define inf 0x3fffffff
 #define smin(a, b)    (a) = min((a), (b))
 #define smax(a, b)    (a) = max((a), (b))

 template<typename T>
 class Matrix {
     public:
         T* p;
         int col, line;
         Matrix():p(NULL), col(), line() {        }
         Matrix(int line, int col):line(line), col(col) {
             p = new T[(const int)(line * col)];
         }

         T* operator [] (int pos) {
             return p + pos * col;
         }
 };

 typedef class Point {
     public:
         int x;
         int y;
         Point(int x = , int y = ):x(x), y(y) {        }
 }Point;

 ifstream fin("puzzle.in");
 ofstream fout("puzzle.out");

 int n, m, q;
 Matrix<boolean> walkable;
 int dis[][][][];

 inline void init() {
     fin >> n >> m >> q;
     walkable = Matrix<boolean>(n, m);
     for(int i = ; i < n; i++)
         for(int j = , x; j < m; j++) {
             fin >> x;
             if(x) walkable[i][j] = true;
             else walkable[i][j] = false;
         }
 }

 const int mov[][] = {{, -, , }, {, , , -}};

 boolean exceeded(int x, int y) {
     if(x <  || x >= n)    return true;
     if(y <  || y >= m)    return true;
     return false;
 }

 int dep[][][][];
 queue<Point> que;
 queue<Point> que1;

 boolean vis1[][];
 int dep1[][];
 inline int bfs1(Point s, Point t, Point g) {
     if(s.x == t.x && s.y == t.y)    return ;
     memset(vis1, false, sizeof(vis1));
     dep1[s.x][s.y] = ;
     vis1[s.x][s.y] = true;
     que.push(s);
     while(!que.empty()) {
         Point e = que.front();
         que.pop();
         for(int i = ; i < ; i++) {
             Point eu(e.x + mov[][i], e.y + mov[][i]);
             if(exceeded(eu.x, eu.y))    continue;
             if(!walkable[eu.x][eu.y])    continue;
             if(vis1[eu.x][eu.y])    continue;
             if(eu.x == g.x && eu.y == g.y)    continue;
             dep1[eu.x][eu.y] = dep1[e.x][e.y] + ;
             if(eu.x == t.x && eu.y == t.y) {
                 while(!que.empty())    que.pop();
                 return dep1[eu.x][eu.y];
             }
             vis1[eu.x][eu.y] = true;
             que.push(eu);
         }
     }
     return -;
 }

 inline void init_dis() {
     for(int i = ; i < n; i++)
         for(int j = ; j < m; j++)
             for(int p = ; p < ; p++) {
                 Point w(i + mov[][p], j + mov[][p]);
                 for(int q = ; q < ; q++) {
                     Point t(i + mov[][q], j + mov[][q]);
                     if(exceeded(w.x, w.y) || exceeded(t.x, t.y))    dis[i][j][p][q] = -;
                     else if(!walkable[w.x][w.y] || !walkable[i][j] || !walkable[t.x][t.y])    dis[i][j][p][q] = -;
                     else if(p == q)    dis[i][j][p][q] = ;
                     else dis[i][j][p][q] = bfs1(w, t, Point(i, j));
                 }
             }
 }

 boolean vis2[][][];
 int f[][][];
 queue<int> que2;
 inline int spfa(Point s, Point t, Point w) {
     memset(vis2, false, sizeof(vis2));
     memset(f, 0x7f, sizeof(f));
     for(int i = ; i < ; i++) {
         Point e(s.x + mov[][i], s.y + mov[][i]);
         if(exceeded(e.x, e.y))    continue;
         if(!walkable[e.x][e.y])    continue;
         f[i][s.x][s.y] = bfs1(Point(w.x, w.y), e, Point(s.x, s.y));
         if(f[i][s.x][s.y] == -)    f[i][s.x][s.y] = 0x7f7f7f7f;
     }
     for(int i = ; i < ; i++) {
         que.push(s);
         que2.push(i);
     }
     while(!que.empty()) {
         Point e = que.front();
         int ed = que2.front();
         que.pop();
         que2.pop();
         vis2[ed][e.x][e.y] = false;
         for(int i = ; i < ; i++) {
             Point eu(e.x + mov[][i], e.y + mov[][i]);
             int eud = i ^ ;
             if(exceeded(eu.x, eu.y))    continue;
             if(!walkable[eu.x][eu.y])    continue;
             if(dis[e.x][e.y][ed][i] == -)    continue;
             if(f[ed][e.x][e.y] + dis[e.x][e.y][ed][i] +  < f[eud][eu.x][eu.y]) {
                 f[eud][eu.x][eu.y] = f[ed][e.x][e.y] + dis[e.x][e.y][ed][i] + ;
                 if(!vis2[eud][eu.x][eu.y]) {
                     vis2[eud][eu.x][eu.y] = true;
                     que.push(eu);
                     que2.push(eud);
                 }
             }
         }
     }
     int ret = inf;
     for(int i = ; i < ; i++)
         smin(ret, f[i][t.x][t.y]);
     if(ret == inf)    return -;
     return ret;
 }

 int res = inf;
 inline void solve() {
     int wx, wy, sx, sy, tx, ty;
     while(q--) {
         res = inf;
         fin >> wx >> wy >> sx >> sy >> tx >> ty;
         wx--, wy--, sx--, sy--, tx--, ty--;
         if(sx == tx && sy == ty) {
             fout << "" << endl;
             continue;
         }
         fout << spfa(Point(sx, sy), Point(tx, ty), Point(wx, wy)) << endl;
     }
 }

 int main() {
     init();
     init_dis();
     solve();
     return ;
 }