MapReduce-皮尔逊(Pearson)线性相关
Pearson相关系数解决了两个群的数据是否线性相关的问题;
先补充一下基本概念:
协方差:如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。

如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差为0的两个随机变量称为是不相关的。
标准差:标准差反应的是个体间(单个变量)的离散程度;

总体相关系数,公式见下方,是由协方差和标准方差计算得来;协方差用于衡量两个变量的总体误差,如果两个变量的变化趋势一致(比如都是大于期望值),则为正值,如果两个变量变化相反(一个大于期望值,一个小于期望值),则为负值;
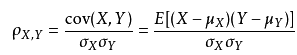
估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母r代表:

r亦可由样本点的标准分数均值估计,得到与上式等价的表达式:
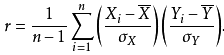
MapReduce-皮尔逊(Pearson)线性相关的更多相关文章
- pandas通过皮尔逊积矩线性相关系数(Pearson's r)计算数据相关性
皮尔逊积矩线性相关系数(Pearson's r)用于计算两组数组之间是否有线性关联,举个例子: a = pd.Series([1,2,3,4,5,6,7,8,9,10]) b = pd.Series( ...
- Pearson(皮尔逊)相关系数
Pearson(皮尔逊)相关系数:也叫pearson积差相关系数.衡量两个连续变量之间的线性相关程度. 当两个变量都是正态连续变量,而且两者之间呈线性关系时,表现这两个变量之间相关程度用积差相关系数, ...
- Pearson(皮尔逊)相关系数及MATLAB实现
转自:http://blog.csdn.net/wsywl/article/details/5727327 由于使用的统计相关系数比较频繁,所以这里就利用几篇文章简单介绍一下这些系数. 相关系数:考察 ...
- np.corrcoef()方法计算数据皮尔逊积矩相关系数(Pearson's r)
上一篇通过公式自己写了一个计算两组数据的皮尔逊积矩相关系数(Pearson's r)的方法,但np已经提供了一个用于计算皮尔逊积矩相关系数(Pearson's r)的方法 np.corrcoef() ...
- 皮尔逊(Pearson)系数矩阵——numpy
一.原理 注意 专有名词.(例如:极高相关) 二.代码 import numpy as np f = open('../file/Pearson.csv', encoding='utf-8') dat ...
- 皮尔逊相似度计算的例子(R语言)
编译最近的协同过滤算法皮尔逊相似度计算.下顺便研究R简单使用的语言.概率统计知识. 一.概率论和统计学概念复习 1)期望值(Expected Value) 由于这里每一个数都是等概率的.所以就当做是数 ...
- 皮尔逊残差 | Pearson residual
参考:Pearson Residuals 这些概念到底是写什么?怎么产生的? 统计学功力太弱了!
- 从欧几里得距离、向量、皮尔逊系数到http://guessthecorrelation.com/
一.欧几里得距离就是向量的距离公式 二.皮尔逊相关系数反应的就是线性相关 游戏http://guessthecorrelation.com/ 的秘诀也就是判断一组点的拟合线的斜率y/x ------- ...
- Python基于皮尔逊系数实现股票预测
# -*- coding: utf-8 -*- """ Created on Mon Dec 2 14:49:59 2018 @author: zhen "&q ...
- Spark Mllib里的如何对两组数据用皮尔逊计算相关系数
不多说,直接上干货! import org.apache.spark.mllib.stat.Statistics 具体,见 Spark Mllib机器学习实战的第4章 Mllib基本数据类型和Mlli ...
随机推荐
- 安全模式下卸载windows installer打包的软件(转)
安全模式下卸载windows installer打包的软件 起因: 主机系统MAC,虚拟软件Parallels Desktop, 虚拟系统 Win 7. 今天在虚拟机WIN7里面安装了某个软件导致重启 ...
- 配置postgres9.3间的fdw——实现不同postgres数据库间的互访问
下面是安装.配置.使用fdw实现postgres数据库间互访问的方法,转载注明出处: 1.源码安装fdw支持(要求数据库源码安装) cd /usr/local/postgresql-9.3.2/con ...
- 015PHP文件处理——文件处理flock 文件锁定 pathinfo realpath tmpfile tempname
<?php /**文件处理flock 文件锁定 pathinfo realpath tmpfile tempname */ /*$arr=pathinfo('ab.txt');//获取文件路径的 ...
- 三个安装,手机看VIP电影。写给亲爱的学习
三个安装,看VIP电影. 市场安装firefox 安装Tempermonkey 打开firefox,点击右上角的三个点,点击附加组件 继续点击浏览全部firefox附加组件 在上面的搜索框输入 tam ...
- 对小波变换中DWT和CWT的理解
转载自 http://blog.sina.com.cn/s/blog_633750d90100hbco.html 连续小波变换的概念.操作.及时间尺度图的显示 最近很多网友问到关于连续小波变换的诸多问 ...
- AngularJS----ngModelController
文档地址:https://docs.angularjs.org/api/ng/type/ngModel.NgModelController 首先声明:DOM value 与view value是完全不 ...
- 1.1.2A+B for Input-Output Practice (II)
A+B for Input-Output Practice (II) Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 ...
- 【微信小程序推广营销】教你微信小程序SEO优化,让你的小程序快人一步抢占先机
今年一月份上线的小程序,经过近一年的沉淀发酵,现在也进入了快速发展期. 在未来肯定会有越来越多的小程序诞生,小程序多了就需要搜索,那么如何让自己的小程序在众多的小程序中脱颖而出,这就需要小程序SEO优 ...
- CentOS 7关闭图形桌面开启文本界面
1,命令模式systemctl set-default multi-user.target 2,图形模式systemctl set-default graphical.target CentOS 7 ...
- CodeForces - 457C:Elections(三分)
You are running for a governor in a small city in Russia. You ran some polls and did some research, ...
