分布式一致性协议之：Gossip（八卦）算法

Gossip算法因为Cassandra而名声大噪，Gossip看似简单，但要真正弄清楚其本质远没看起来那么容易。为了寻求Gossip的本质，下面的内容主要参考Gossip的原始论文：<<Efficient Reconciliation and Flow Control for Anti-Entropy Protocols>>。

1. Gossip背景

Gossip算法如其名，灵感来自办公室八卦，只要一个人八卦一下，在有限的时间内所有的人都会知道该八卦的信息，这种方式也与病毒传播类似，因此Gossip有众多的别名“闲话算法”、“疫情传播算法”、“病毒感染算法”、“谣言传播算法”。

但Gossip并不是一个新东西，之前的泛洪查找、路由算法都归属于这个范畴，不同的是Gossip给这类算法提供了明确的语义、具体实施方法及收敛性证明。

2. Gossip特点

Gossip算法又被称为反熵（shang）（Anti-Entropy），熵是物理学上的一个概念，代表杂乱无章，而反熵就是在杂乱无章中寻求一致，这充分说明了Gossip的特点：在一个有界网络中，每个节点都随机地与其他节点通信，经过一番杂乱无章的通信，最终所有节点的状态都会达成一致。每个节点可能知道所有其他节点，也可能仅知道几个邻居节点，只要这些节可以通过网络连通，最终他们的状态都是一致的，当然这也是疫情传播的特点。

要注意到的一点是，即使有的节点因宕机而重启，有新节点加入，但经过一段时间后，这些节点的状态也会与其他节点达成一致，也就是说，Gossip天然具有分布式容错的优点。

3. Gossip本质

Gossip是一个带冗余的容错算法，更进一步，Gossip是一个最终一致性算法。虽然无法保证在某个时刻所有节点状态一致，但可以保证在”最终“所有节点一致，”最终“是一个现实中存在，但理论上无法证明的时间点。

因为Gossip不要求节点知道所有其他节点，因此又具有去中心化的特点，节点之间完全对等，不需要任何的中心节点。实际上Gossip可以用于众多能接受“最终一致性”的领域：失败检测、路由同步、Pub/Sub、动态负载均衡。

但Gossip的缺点也很明显，冗余通信会对网路带宽、CUP资源造成很大的负载，而这些负载又受限于通信频率，该频率又影响着算法收敛的速度，后面我们会讲在各种场合下的优化方法。

4. Gossip节点的通信方式及收敛性

根据原论文，两个节点（A、B）之间存在三种通信方式:

push: A节点将数据(key,value,version)及对应的版本号推送给B节点，B节点更新A中比自己新的数据
pull：A仅将数据key,version推送给B，B将本地比A新的数据（Key,value,version）推送给A，A更新本地
push/pull：与pull类似，只是多了一步，A再将本地比B新的数据推送给B，B更新本地

如果把两个节点数据同步一次定义为一个周期，则在一个周期内，push需通信1次，pull需2次，push/pull则需3次，从效果上来讲，push/pull最好，理论上一个周期内可以使两个节点完全一致。直观上也感觉，push/pull的收敛速度是最快的。

假设每个节点通信周期都能选择（感染）一个新节点，则Gossip算法退化为一个二分查找过程，每个周期构成一个平衡二叉树，收敛速度为O(n² )，对应的时间开销则为O(logⁿ )。这也是Gossip理论上最优的收敛速度。但在实际情况中最优收敛速度是很难达到的，假设某个节点在第i个周期被感染的概率为p_i ,第i+1个周期被感染的概率为p_i+1 ，则pull的方式:

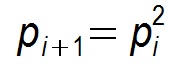
而push为：

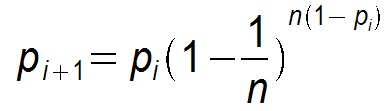
显然pull的收敛速度大于push，而每个节点在每个周期被感染的概率都是固定的p(0<p<1)，因此Gossip算法是基于p的平方收敛，也成为概率收敛，这在众多的一致性算法中是非常独特的。

个Gossip的节点的工作方式又分两种：

Anti-Entropy（反熵）：以固定的概率传播所有的数据
Rumor-Mongering（谣言传播）：仅传播新到达的数据

Anti-Entropy模式有完全的容错性，但有较大的网络、CPU负载；Rumor-Mongering模式有较小的网络、CPU负载，但必须为数据定义”最新“的边界，并且难以保证完全容错，对失败重启且超过”最新“期限的节点，无法保证最终一致性，或需要引入额外的机制处理不一致性。我们后续着重讨论Anti-Entropy模式的优化。

5. Anti-Entropy的协调机制

协调机制是讨论在每次2个节点通信时，如何交换数据能达到最快的一致性，也即消除两个节点的不一致性。上面所讲的push、pull等是通信方式，协调是在通信方式下的数据交换机制。协调所面临的最大问题是，因为受限于网络负载，不可能每次都把一个节点上的数据发送给另外一个节点，也即每个Gossip的消息大小都有上限。在有限的空间上有效率地交换所有的消息是协调要解决的主要问题。

在讨论之前先声明几个概念：

令N = {p,q,s,...}为需要gossip通信的server集合，有界大小
令(p1,p2,...)是宿主在节点p上的数据，其中数据有(key,value,version)构成，q的规则与p类似。

为了保证一致性，规定数据的value及version只有宿主节点才能修改，其他节点只能间接通过Gossip协议来请求数据对应的宿主节点修改。

5.1 精确协调（Precise Reconciliation）

精确协调希望在每次通信周期内都非常准确地消除双方的不一致性，具体表现为相互发送对方需要更新的数据，因为每个节点都在并发与多个节点通信，理论上精确协调很难做到。精确协调需要给每个数据项独立地维护自己的version，在每次交互是把所有的(key,value,version)发送到目标进行比对，从而找出双方不同之处从而更新。但因为Gossip消息存在大小限制，因此每次选择发送哪些数据就成了问题。当然可以随机选择一部分数据，也可确定性的选择数据。对确定性的选择而言，可以有最老优先（根据版本）和最新优先两种，最老优先会优先更新版本最新的数据，而最新更新正好相反，这样会造成老数据始终得不到机会更新，也即饥饿。

当然，开发这也可根据业务场景构造自己的选择算法，但始终都无法避免消息量过多的问题。

5.2 整体协调（Scuttlebutt Reconciliation）

整体协调与精确协调不同之处是，整体协调不是为每个数据都维护单独的版本号，而是为每个节点上的宿主数据维护统一的version。比如节点P会为(p1,p2,...)维护一个一致的全局version，相当于把所有的宿主数据看作一个整体，当与其他节点进行比较时，只需必须这些宿主数据的最高version，如果最高version相同说明这部分数据全部一致，否则再进行精确协调。

整体协调对数据的选择也有两种方法：

广度优先：根据整体version大小排序，也称为公平选择
深度优先：根据包含数据多少的排序，也称为非公平选择。因为后者更有实用价值，所以原论文更鼓励后者

6. Cassandra中的实现

经过验证，Cassandra实现了基于整体协调的push/push模式，有几个组件：

三条消息分别对应push/pull的三个阶段：

GossipDigitsMessage
GossipDigitsAckMessage
GossipDigitsAck2Message

还有三种状态：

EndpointState：维护宿主数据的全局version，并封装了HeartBeat和ApplicationState
HeartBeat：心跳信息
ApplicationState：系统负载信息（磁盘使用率）

Cassandra主要是使用Gossip完成三方面的功能：

失败检测
动态负载均衡
去中心化的弹性扩展

7. 总结

Gossip是一种去中心化、容错而又最终一致性的绝妙算法，其收敛性不但得到证明还具有指数级的收敛速度。使用Gossip的系统可以很容易的把Server扩展到更多的节点，满足弹性扩展轻而易举。

唯一的缺点是收敛是最终一致性，不使用那些强一致性的场景，比如2pc。