K - Ancient Messages(dfs求联通块)

K - Ancient Messages

Time Limit:3000MS Memory Limit:0KB 64bit IO Format:%lld & %llu

Appoint description:

Description

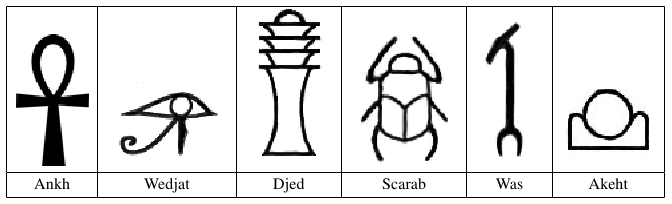
In order to understand early civilizations, archaeologists often study texts written in ancient languages. One such language, used in Egypt more than 3000 years ago, is based on characters called hieroglyphs. Figure C.1 shows six hieroglyphs and their names. In this problem, you will write a program to recognize these six characters.

Figure C.1: Six hieroglyphs

Input

The input consists of several test cases, each of which describes an image containing one or more hieroglyphs chosen from among those shown in Figure C.1. The image is given in the form of a series of horizontal scan lines consisting of black pixels (represented by 1) and white pixels (represented by 0). In the input data, each scan line is encoded in hexadecimal notation. For example, the sequence of eight pixels 10011100 (one black pixel, followed by two white pixels, and so on) would be represented in hexadecimal notation as 9c. Only digits and lowercase letters a through f are used in the hexadecimal encoding. The first line of each test case contains two integers, H and W. H(0 < H200) is the number of scan lines in the image. W(0 < W50) is the number of hexadecimal characters in each line. The next H lines contain the hexadecimal characters of the image, working from top to bottom. Input images conform to the following rules:

The image contains only hieroglyphs shown in Figure C.1.
Each image contains at least one valid hieroglyph.
Each black pixel in the image is part of a valid hieroglyph.
Each hieroglyph consists of a connected set of black pixels and each black pixel has at least one other black pixel on its top, bottom, left, or right side.
The hieroglyphs do not touch and no hieroglyph is inside another hieroglyph.
Two black pixels that touch diagonally will always have a common touching black pixel.
The hieroglyphs may be distorted but each has a shape that is topologically equivalent to one of the symbols in Figure C.1. (Two figures are topologically equivalent if each can be transformed into the other by stretching without tearing.)

The last test case is followed by a line containing two zeros.

Output

For each test case, display its case number followed by a string
containing one character for each hieroglyph recognized in the image,
using the following code:

Ankh: A
Wedjat: J
Djed: D
Scarab: S
Was: W
Akhet: K

In each output string, print the codes in alphabetic order. Follow the format of the sample output.

The sample input contains descriptions of test cases shown in Figures
C.2 and C.3. Due to space constraints not all of the sample input can be
shown on this page.

Sample Input

100 25

0000000000000000000000000

0000000000000000000000000

...(50 lines omitted)...

00001fe0000000000007c0000

00003fe0000000000007c0000

...(44 lines omitted)...

0000000000000000000000000

0000000000000000000000000

150 38

00000000000000000000000000000000000000

00000000000000000000000000000000000000

...(75 lines omitted)...

0000000003fffffffffffffffff00000000000

0000000003fffffffffffffffff00000000000

...(69 lines omitted)...

00000000000000000000000000000000000000

00000000000000000000000000000000000000

0 0

Sample Output

Case 1: AKW

Case 2: AAAAA

 #include <iostream>

 #include <cstdio>

 #include <cstring>

 #include <cmath>

 #include <algorithm>

 #include <string>

 #include <vector>

 #include <stack>

 #include <queue>

 #include <set>

 #include <map>

 #include <list>

 #include <iomanip>

 #include <cstdlib>

 #include <sstream>

 using namespace std;

 const int INF=0x5fffffff;

 const double EXP=1e-;

 const int maxh=;

 const int maxw=*+;

 int H,W;

 int pic[maxh][maxw],color[maxh][maxw];

 int dir[][]={{,},{,},{,-},{-,}};

 char bin[][];

 char line[maxw];

 const char* code = "WAKJSD";

 void decode(int row,int col,char c)

 {

     for(int i=;i<;i++)

     {

         pic[row][col+i]=bin[(int)c][i]-'';

     }

 }

 void dfs(int row,int col,int c)

 {

     color[row][col]=c;

     for(int i=;i<;i++)

     {

         int x=row+dir[i][];

         int y=col+dir[i][];

         if(x>=&&x<H&&y>=&&y<W&&pic[x][y]==pic[row][col]&&color[x][y]==)

             dfs(x,y,c);

     }

 }

 vector<set<int> > neighbor;

 void check(int row,int col)    //check white

 {

     for(int i=;i<;i++)

     {

         int x=row+dir[i][];

         int y=col+dir[i][];

         if(x>=&&x<H&&y>=&&y<W&&pic[x][y]==&&color[x][y]!=)

             neighbor[color[row][col]].insert(color[x][y]);

     }

 }

 char recognize(int c)

 {

     int cnt=neighbor[c].size();

     return code[cnt];

 }

 int main()

 {

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin[''], "");

     strcpy(bin['a'], "");

     strcpy(bin['b'], "");

     strcpy(bin['c'], "");

     strcpy(bin['d'], "");

     strcpy(bin['e'], "");

     strcpy(bin['f'], "");

     int kase=;

     while(scanf("%d%d",&H,&W)==&&(H+W))

     {

         memset(pic,,sizeof(pic));

         memset(color,,sizeof(color));

         for(int i=;i<H;i++)

         {

             scanf("%s",line);

             for(int j=;j<W;j++)

                 decode(i+,j*+,line[j]);   //注意起始位置

         }

         H+=;

         W=W*+;

         int cnt=;

         vector<int >  c;

         for(int i=;i<H;i++)

             for(int j=;j<W;j++)

         {

             if(color[i][j]==)

             {

                 dfs(i,j,++cnt);

                 if(pic[i][j]==)

                     c.push_back(cnt);

             }

         }

         neighbor.clear();

         neighbor.resize(cnt+);

         for(int i=;i<H;i++)

             for(int j=;j<W;j++)

         {

             if(pic[i][j]==)

                 check(i,j);

         }

         vector<char>  ans;

         int t=c.size();

         for(int i=;i<t;i++)

             ans.push_back(recognize(c[i]));

         sort(ans.begin(),ans.end());

         printf("Case %d: ",kase++);

         for(int i=;i<t;i++)

             printf("%c",ans[i]);

         printf("\n");

     }

     return ;

 }