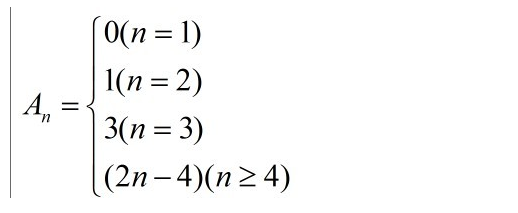阿里巴巴2013年实习生笔试题A
一、单项选择题
1.下列说法不正确的是:(B)
A.SATA硬盘的速度速度大约为500Mbps/s
B.读取18XDVD光盘数据的速度为1Gbps
C.前兆以太网的数据读取速度为1Gpbs
D.读取DDR3内存数据的速度为100Gbps
解析:有说B的,有说D的,B肯定是不对的吧。
关于B选项:
理论上讲:DVD的1倍速是1350KB/s,CD是150KB/s,DVD的1倍速等于CD的9倍速。
因为CD容量是700MB左右,DVD单面单层(DVD-5)是4.7GB(实际为4.37GB),DVD单面单层的容量是CD的6.4倍左右,所以,1倍速的播放器在80分钟内把一张700MB的CD读取出来(700MB*1024/150KB/s/60=79.6min),1倍速的播放器在60分钟内把一张4.7GB的DVD读出来(4.37GB*1024*1024、1350KB/s/60=56.6min)
DVD的倍速:
1x:(1倍速)基本传输速率为1350KB/s。
2x:(2倍速)基本传输速率为2700KB/s。
4x:(4倍速)基本传输速率为5400KB/s。
18x:(18倍速)基本传输速率为24300KB/s=23M。
CD的倍速:
1x(1倍速)基本传输速率为150KB/s。
2x(2倍速)基本传输速率为300KB/s
4x(4倍速)基本传输速率为600KB/s。
8x(8倍速)基本传输速率为1200KB/s。
2.(D)不能用于Linux中的进程通信
A.共享内存
B.命名管道
C.信号量
D.临界区(每个进程访问临界资源的那段代码称为临界区;临界资源就是每次只允许一个进程访问的共享资源)
解析:
Linux进程间通信的几种主要手段简介:
(1)管道及有名管道:管道可用于具有亲缘关系的进程间通信;有名管道克服了管道没有名字的限制,因此,除了具有管道所具有的功能外,它还允许无亲缘关系进程间通信;
(2)信号:信号是比较复杂的通信方式,用于通知接收有某种事件发生,除了用于进程间通信外,进程还可以发送信号给进程本身;linux除了支持Unix早期信号语义函数signal外,还支持语义符合Posix标准的信号函数sigaction(实际上,该函数是基于BSD的,BSD为了实现可靠信号机制,又能够统一对外接口,用sigaction函数重新实现了signal函数);
(3)消息队列:消息队列是消息的链接表,包括Posix消息队列和system V消息队列。有足够权限的进程可以向队列中添加消息,被赋予读权限的进程则可以读走队列中的消息。消息队列客服了信号承载信息量少,管道只能承载无格式字节流以及缓冲区大小受限等缺点;
(4)共享内存:使得多个进程可以访问同一块内存空间,是最快的可用IPC形式。是针对其他通信机制运行效率较低而设计的。往往与其他通信机制,如信息量结合使用,来达到进程间的同步及互斥;
(5)信息量:主要作为进程间以及同一进程不同线程之间的同步手段;
(6)套接口:更为一般的进程间通信机制,可用于不同机器之间的进程间通信。
Linux线程间通信几种主要通信手段简介:
(1)锁机制:包括互斥锁、条件变量、读写锁,互斥锁提供了以排他方式防止数据结构被并发修改的方法,使用条件变量可以以原子的方式阻塞线程,直到某个特定条件为真为止。对条件的测试是在互斥锁的保护下进行的,条件变量始终与互斥锁一起使用。读写锁运行多个线程同时读共享数据,而对写操作是互斥的;
(2)信号量机制:包括无名线程信号量和命名线程信号量;
(3)信号机制:类似于进程间的信号处理;
进程与线程的区别:
进程概念:
进程是表示资源分配的基本单位,又是调度运行的基本单位。例如,用户运行自己的程序,系统就创建一个进程,并为它分配资源。然后,把该进程放入进程的就绪队列。进程调度程序选中它,为它分配CPU以及其他有关子亚U年,该进程才真正运行。所以,进程是系统中并发执行的单位。
线程的概念:
线程是进程中执行运算的最小单位,亦即执行处理机调度的基本单位。如果把进程理解为在逻辑上操作系统所完成的任务,那么线程表示完成该任务的许多子任务之一。线程可以在处理器上独立调度执行,这样,在多处理器环境下就允许几个线程各自在单独处理器上进行。
引入线程的好处:
(1)易于调度。
(2)提高并发性。通过线程可方便有效地实现并发性。进程可创建多个线程来执行同一程序的不同部分。
(3)开销少。创建线程比创建进程要快,所需开销很少。
(4)利于充分发挥多处理器的功能。通过创建多线程进程(即一个进程可具有两个或更多个线程),每个线程在一个处理器上运行,从而实现应用程序的并发性,使每个处理器都得到充分运行。
进程和线程的关系:
(1)一个线程只能属于一个进程,而一个进程可以有多个线程,但至少有一个线程。
(2)资源分配给进程,同一进程的所有线程共享该进程的所有资源。
(3)处理机分给线程,即真正在处理机上运行的是线程。
(4)线程在执行过程中,需要协作同步。不同进程的线程间要利用消息通信的办法实现同步。
3.设在内存中有P1,P2,P3三道程序,并按照P1,P2,P3的优先级次序运行,其中内部计算和IO操作时间由下表给出(CPU计算和IO资源都只能同时由一个程序占用):
P1:计算60ms---》IO 80ms---》计算20ms
P2:计算120ms---》IO 40ms---》计算40ms
P3:计算40ms---》IO 80ms---》计算40ms
完成三道程序比单道运行节省的时间是(C)
A.80ms B.120ms C.160ms D.200ms
解析:
单道运行的总时间为:60+80+20+120+40+40+40+80+40=520ms
4.两个等价线程并发的执行下列程序,a为全局变量,初始为0,假设printf、++、--操作都是原子性的,则输出不肯哪个是(A)
void foo() {
if(a <= ) {
a++;
}
else {
a--;
}
printf("%d", a);
}
A.01 B.10 C.12 D.22
解析:
对于B选项:P1执行程序,输入1,P2执行程序,输出0;
对于C选项:初始为0,P1执行完判断语句,决定要执行a++,中断,P2进行判断,此时a仍然等于0,执行判断语句,并执行输入,得到1,P1然后继续执行,此时它该执行a++,这时a=1,执行并输出,结果为2;
对于D答案:初始为0,P1执行完判断语句,决定要执行a++,中断,P2进行判断,此时a仍然等于0,执行a++,得到a=1,中断,P1继续执行a++,a=2,P1输出,得到2,P1结束,P2继续执行输出语句,得到2;
5.给定fun函数如下,那么fun(10)的输出结果是(C)
int fun(int x)
{
return (x==1) ? 1 : (x + fun(x-1));
}
A.0 B.10 C.55 D.3628800
6.在c++程序中,如果一个整型变量频繁使用,最好将他定义为(D)
A.auto B.extern C.static D.register
解析:
C语言提供了四种类型修饰符:auto、register、extern、static。
auto修饰仅在语句块内使用,初始化可为任何表达式,其特定是当执行流程进入该语句块的时候执行初始化操作,没有默认值;
使用register修饰符修饰变量,将暗示编译程序相应的变量被频繁地使用,如果可能的话,应将其保存到CPU的寄存器,以加快其存储速度;
static静态变量声明符。在声明它的语句块、子程序块或函数内部有效,值保持,在整个程序期间分配存储器空间,编译器默认值为0,。是C/C++中很常用的修饰符,它被用来控制变量的存储方式和可见性。Static被引入以告知编译器,将变量存储在程序的静态存储区而非栈上空间。
extern可以置于变量或者函数前,以表示变量或者函数的定义在别的文件中,提示编译器遇到此变量或函数时,在其他模块中寻找其定义。另外,extern也可用来进行链接指定。
7.长为n的字符串中匹配长度为m的子串的复杂度为(B)
A.O(N) B.O(M+N) C.O(N+LOGM) D.O(M+LOGN)
解析:有选B的,也有选C的。
这道题目首先想到的是KMP算法,时间复杂度为O(m+n)。但是还有的选择C选项,貌似是Sunday算法。
8.判断一包含n个整数a[]中是否存在i、j、k满足a[i] + a[j] = a[k]的时间复杂度为(B)
A.O(n) B.O(n^2) C.O(nlog(n)) D.O(n^2log(n))
解析:
对于B选项,可以这样实现。
(1)先对数组进行排序,时间为O(nlogn),然后从大往小取a[k],n次
然后在0到k-1之间夹出i,j来...每次K操作...若存在负数,则需要在0到n-1之间夹出i,j;
(2)先对数组进行排序,时间为O(nlogn),然后两次for循环嵌套,进行hash查找;
对于D选项,可以这样实现。
(1)先对数组进行排序,时间为O(nlogn),然后两个for循环嵌套,二分查找a[i]+a[j]是否在数组中;
9.三次射击能中一次的概率是0.95,请问一次射击能中的概率是多少?(C)
A.0.32 B.0.5 C.0.63 D.0.85
解析:
公式很简单,1-(1-p)^3=0.95。接下来需要有一定的估算技巧。A选项可以看作1/3,C选项可以看作2/3,D选项可以看作4/5.
10.下列序排算法中最坏复杂度不是n(n-1)/2的是(D)
A.快速序排 B.冒泡序排 C.直接插入序排 D.堆序排
解析:
各种排序算法的时间复杂度:
插入排序思想:
将n个元素的数列分为已有序和无序两个部分,每次处理就是讲无序数列中的第一个元素与有序数列的元素从后往前逐个进行比较,找到插入位置,将该元素插入到有序数列的合适位置。
希尔排序思想:
希尔排序,也称为递减增量排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
(1)插入排序在对几乎已经排好序的数据操作时,效率高,即可达到线性排序的效率;
(2)但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
选择排序思想:
首先在未排序的序列中找到最大(小)元素,存放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最大(小)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
二、不定向选择题
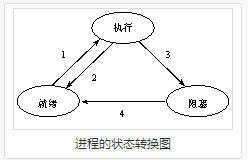
1.以下哪些进程状态转换是正确的(ABCE)
A.就绪到运行 B.运行到就绪 C.运行到阻塞 D.阻塞到运行 E.阻塞到就绪
解析:
进程调度:
四种进程间的状态转换:
就绪—>执行 执行—>阻塞 阻塞—>就绪 执行—>就绪
1)进程的三种基本状态
进程在运行中不断地改变其运行状态。通常,一个进程必须具有以下三种基本状态:
就绪状态:
当进程已分配到除CPU以外的所有必要的资源,只要获得处理机便可立即执行,这时的进程状态就称为就绪状态;
执行状态:
当进程已获得处理机,其程序正在处理机上执行,此时的进程状态称为执行状态;
阻塞状态:
正在执行的进程,由于等待某个事件发生而无法执行时,便放弃处理机而进入阻塞状态。引起进程阻塞的事件有很多种,例如,等待I/O完成、申请缓冲区不能满足、等待信号等。
2)进程三种状态间的转换
一个进程在运行期间,不断地从一种状态转换到另一种状态,它可以多次处于就绪状态和执行状态,也可以多次处于阻塞状态。
A. 就绪—>执行
处于就绪状态的进程,当进程调度程序为之分配好了处理机后,该进程便由就绪状态转换为执行状态;
B. 执行—>就绪
处于执行状态的进程在其执行过程中,因分配给它的一个时间片已经用完而不得不让出处理机,于是进程从执行状态转换为就绪状态;
C. 执行—>阻塞
正在执行的进程因等待某种事件发生而无法继续执行时,便从执行状态变成阻塞状态;
D. 阻塞—>就绪
处于阻塞状态的进程,若其等待的事件已经发生,于是进程便从阻塞状态转变为就绪状态。
4.A和B晚上无聊就开始数星星。每次只能数K个(20<=k<=30)A和B轮流数。最后谁把星星数完谁就获胜,那么当星星数量为多少时候A必胜?()
A、2013 B、2888 C、4062 D、*** E、****
解析:不懂
对于上述答案,A有必胜的策略,A、B、C、D、E都应该选择。首先,A选取,使剩余的星星为50的倍数。然后数星星的顺序为B、A、B、A......。B数k个星星,则A就数50-k个,使剩余星星始终剩余为50的倍数,最后,一定是A数最后的星星。A必胜。
三、填空问答题
1.给你一个整型数组A[N],完成一个小程序代码(20行之内),使得A[N]逆向,即原数组为1,2,3,4,逆向之后为4,3,2,1。
3.有个苦逼的上班族,他每天忘记定闹钟的概率为0.2,上班堵车的概率为0.5,如果他既没定闹钟上班又堵车那他迟到的概率为1.0,如果他定了闹钟但是上班堵车那他迟到的概率为0.9,如果他没定闹钟但是上班不堵车他迟到的概率为0.8,如果他既定了闹钟上班又不堵车那他迟到的概率为0.0,那么求出他在60天里上班迟到的期望。
解析:概率为0.54 (说明:先前此处写的是0.51,若带来误导,这里对各位说声抱歉,对不起)
4.战报交流:战场上不同的位置有N个战士(n>4),每个战士知道当前的一些战况,现在需要这n个战士通过通话交流,互相传达自己知道的战况信息,每次通话,可以让通话的双方知道对方的所有情报,设计算法,使用最少的通话次数,是的战场上的n个士兵知道所有的战况信息,不需要写程序代码,得出最少的通话次数。
解析:
笔试的时候是这样想的:N-1个人围成一个环,将知道的消息都告诉第N个人,需要N-1次,同时第N-1个人与第N个人交流时,两人互相交流消息,这样子第N-1个人与第N个人都知道了所有人的信息,接下来第N-1人沿着环将消息传递下去,需要N-2次,所以需要N-1+(N-2)=2N-3。
但是实际上这个问题有着更优的解法。
扩展的一类问题:
题目:假如我们班有n个MM,每一个MM都有一个独家的八卦消息。两个MM可以通过电话联系,一通电话将使得双方都获知对方目前已经知道的全部消息。要想所有n个MM都知道所有n条八卦消息,最少需要多少通电话?请给出通话方案。
来自:http://www.matrix67.com/blog/archives/1078
解答:
(1)分析情况
当n很小时我们很容易通过枚举的方法找出最佳通话方案:
A1=0 A2=1 A3=3 A4=4 A5=6 A6=8
(2)基于中间消息传递人的思想建模
可以先把所有消息集中于一个或几个人,然后再由这些消息汇总人把消息传给所有人。设n个MM中有m个消息汇总人,她们共享所有消息需要打An通电话。
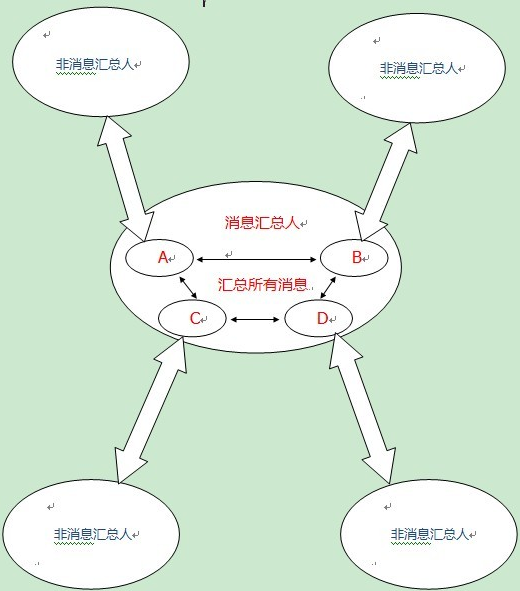
通话方案如下:
第一、剩下的n-m个MM每个人从m个消息汇总人中随机选择一个通话。这样一来m个消息汇总人就掌握所有n条八卦消息,并且她们每个人所掌握的消息互不重叠,是互补的;
第二、m个消息汇总人通过打电话共享所有八卦消息;
第三、作为消息汇总人的m个MM再通过电话将自己新得到八卦新闻告知最开始打电话给自己的MM,使得她们也掌握所有n条消息;
模型如下:
(3)模型分析
按照上面的通话方案,第一步需要n-m通电话,第二步需要Am通电话,第三步需要n-m通电话,故有An=2*(n-m)+Am,进一步化简得
An=2*n - (2*m - Am)
即当MM的个数为n时,共享所有八卦消息共需要2*n - (2*m - Am)通电话。若要使得通话次数最小,就要求(2*m - Am)最大。因此,取多少个MM作为消息汇总人使得(2*m - Am)最大成为了解决这个问题的关键,它反映了MM们之间通话的效率。记Em=(2*m - Am)。
当有一个消息汇总人即m=1时,E1=2*1 - A1=2;
当有两个消息汇总人即m=2时,E2=2*2 - A2=3;
m=3时,E3=2*3 - A3=3;
m=4时,E4=2*4 - A4=4;
m=5时,E5=2*5 - A5=4;
m=6时,E6=2*6 - A6=4;
.......
由归纳法可知,当m>=4时,Em有最大值4,An有最小值2*n - 4,即当有大于或等于4个消息汇总人时可通过上述通话方案使得n个MM通过最小的电话数共享所有八卦消息。此时共需要2*n - 4次电话。
(4)模型证明
http://blog.csdn.net/linygood/article/details/8898844
(5)模型结果
题目中如果告诉n大于4,那么结果就是2n-4。
5.有N个人,其中一个明星和n-1个群众,群众都认识明星,明星不认识任何群众,群众和群众之间的认识关系不知道,现在如果你是机器人R2T2,你每次问一个人是否认识另外一个人的代价为O(1),试设计一种算法找出明星,并给出时间复杂度(没有复杂度不得分)。
解答:
这个问题等价于找未知序列数中的最小数,我们将reg这个函数等价为以下过程:如果i认识j,记作i大于等于j,同样j不一定大于等于i,满足要求,i不认识j记作i<j,对明星k,他不认识所有人,则k是其中最小的数,且满足其余的人都认识他,也就是其余的人都大于等于k.这样问题就被转换了。就拿N=5来说,首先有数组S[5]={A,B,C,D,E}这5个变量,里边存放着随机数,求是否存在唯一最小数,如果存在位置在S中的哪里。(楼主这里是这个意思,按我的理解题中这个最小数一定是存在且唯一的)。
另外一种思路:
四、综合题
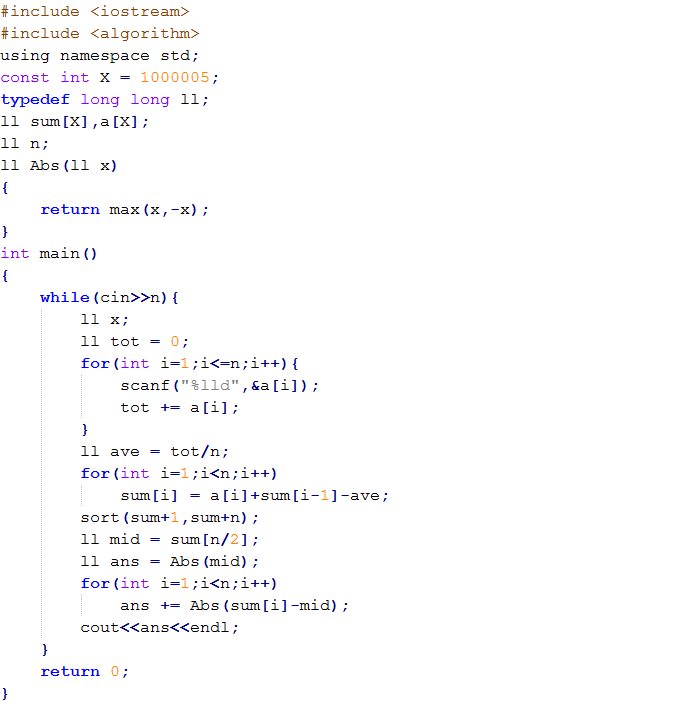
有一个淘宝商户,在某城市有n个仓库,每个仓库的储货量不同,现在要通过货物运输,将每次仓库的储货量变成一致的,n个仓库之间的运输线路围城一个圈,即1->2->3->4->...->n->1->...,货物只能通过连接的仓库运输,设计最小的运送成本(运货量*路程)达到淘宝商户的要求,并写出代码。
解答:
这个题目类似的题目有:
题目:http://www.lydsy.com/JudgeOnline/problem.php?id=1045
有n个小朋友坐成一圈,每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为1,求使所有人获得均等糖果的最小代价。
分析:
假设a1分给an的糖果数为k,则可以得到以下的信息:
a1 a2 a3 an-1 an
当前数目:a1-k a2 a3 an-1 an+k
所需代价:|a1-k-ave| |a1+a2-k-2*ave| |a1+a2+a3-k-3*ave||a1+..+a(n-1)-k-(n-1)*ave| |k|
以sum[i]表示从a1加到ai减掉i*ave的和值,这以上可以化简为
总代价 = |s1-k|+|s2-k|+...+|s(n-1)-k|+|k|
不难看出:当k为s1...s(n-1)中的中位数的时候,所需的代价最小
转载请注明:http://www.cnblogs.com/iloveyouforever/
阿里巴巴2013年实习生笔试题A的更多相关文章
- 阿里巴巴2013年实习生笔试题B
阿里巴巴集团2013实习生招聘技术类笔试题(B) 一.单向选择题 1.在常用的网络协议中,___B__是面向连接的.有重传功能的协议. A. IP B. TCP C. UDP D. DXP 2.500 ...
- [NOIp 1998 提高组]Probelm 2 连接多位数【2011百度实习生笔试题】
/*====================================================================== [NOIp 1998 提高组]Probelm 2 连接 ...
- Microsoft 2013校园招聘笔试题及解答
Microsoft 2013校园招聘笔试题及解答 题目是自己做的,求讨论.吐槽.拍砖 1. Which of the following callingconvension(s) suppo ...
- 诺基亚(Microsoft Devices Group)2014暑期实习生笔试题知识点
总结一下Microsoft Devices Group的软件类笔试题,全部笔试题分两份试卷,逻辑题一份和软件測试题一份,仅仅总结技术题喽~题目全英文,仅仅包括选择题和填空题.选择题居多.分单选和多选. ...
- 2014腾讯实习生笔试题——define与typedef
2014腾讯实习生笔试(广州站)第26题填空题: #define MAX_NUM 1000+1 int Temp = Max_NUM*10; 则Temp的值为( ) 答案是:1010, 由于宏定义仅仅 ...
- Java类的连接与初始化 (及2013阿里初始化笔试题解析)
Java虚拟机通过装载.连接.初始化来使得一个Java类型可以被Java程序所使用,如下图所示,其中连接过程又分为验证.准备.解析三个部分.其中部分类的解析过程可以推迟到程序真正使用其某个符号引用时再 ...
- PayPal2019春招实习生笔试题的某一题
题目简单描述:给你n个点的坐标(x, y),均为浮点数. 如果任意两个点之间的欧几里得距离小于给定的一个浮点值,则认为这两个点之间有关联,并且关联具有传递性,总之就是尽可能扩大一个集合. 输入: d ...
- Java工程师笔试题整理[校招篇]
Java工程师笔试题整理[校招篇] 隔着两个月即将开始校招了.你是不是也想借着这个机会崭露头角,拿到某些大厂的offer,赢取白富美.走上人生巅峰?当然如果你还没能打下Java基础,一定要先打 ...
- 代写编程的作业、笔试题、课程设计,包括但不限于C/C++/Python
代写编程作业/笔试题/课程设计,包括但不限于C/C++/Python 先写代码再给钱,不要任何定金!价钱公道,具体见图,诚信第一! (截止2016-11-22已接12单,顺利完成!后文有成功交付的聊天 ...
随机推荐
- 销售订单行上行号LINE_SHIPMENT_OPTION_NUMBER
销售订单行上行号:LINE_SHIPMENT_OPTION_NUMBER 取值: ( 1) Line块的块级触发器POST-QUERY调用: OE_LINE.Post_Query;(来自于库OE ...
- Design Mode 之 结构模式
这里我们主要介绍7种结构型模式:适配器模式.装饰模式.代理模式.外观模式.桥接模式.组合模式.享元模式.其中对象的适配器模式是各种模式的起源,我们看下面的图: B1.适配器模式(Adapter) 模式 ...
- JavaScript 之 执行前台函数
1.OnClientClick (vs2003不支持这个方法) <asp:Button ID="Button" runat="server" Text=& ...
- date类型时间比较大小
#方法一Date1.after(Date2),当Date1大于Date2时,返回TRUE,当小于等于时,返回false:Date1.before(Date2),当Date1小于Date2时,返回TRU ...
- Java开发核心技术面试心得分析
Java的数据结构有哪些?Map与Set的本质区别是什么? 分析:Java常见的数据结构有Collection和Map,其中Collection接口下包括List和Set接口,其下又有多个实现类如Li ...
- 重构22-Break Method(重构方法)
这个重构是一种元重构(meta-refactoring),它只是不停地使用提取方法重构,直到将一个大的方法分解成若干个小的方法.下面的例子有点做作,AcceptPayment方法没有丰富的功能.因此为 ...
- 基本java类-In.java
package com.algorithm.api; /************************************************************************ ...
- Node.js学习笔记(1)
Node是用c++语言开发,能运行javascript语言的环境. 使用的时候格式为node helloworld.js,helloword.js为服务器端或者系统级端的javascript代码. N ...
- poj 1698 Alice's Chance 最大流
题目:给出n部电影的可以在周几拍摄.总天数.期限,问能不能把n部电影接下来. 分析: 对于每部电影连上源点,流量为总天数. 对于每一天建立一个点,连上汇点,流量为为1. 对于每部电影,如果可以在该天拍 ...
- 结合setTimeout和clearTimeout,实现“返回顶部”的功能
结合setTimeout和clearTimeout,当页面停止滚动时,“返回顶部”按钮淡隐淡出.点击“返回顶部”页面以动画形式返回顶部.完美兼容ie6-11,firefox,chrome等. html ...