HDU 4676 Sum Of Gcd 【莫队 + 欧拉】

任意门：http://acm.hdu.edu.cn/showproblem.php?pid=4676

Sum Of Gcd

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 908    Accepted Submission(s): 438

Problem Description

Given you a sequence of number a₁, a₂, ..., a_n, which is a permutation of 1...n.
You need to answer some queries, each with the following format:
Give you two numbers L, R, you should calculate sum of gcd(a[i], a[j]) for every L <= i < j <= R.

 

Input

First line contains a number T(T <= 10),denote the number of test cases.
Then follow T test cases.
For each test cases,the first line contains a number n(1<=n<= 20000).
The second line contains n number a₁,a₂,...,a_n.
The third line contains a number Q(1<=Q<=20000) denoting the number of queries.
Then Q lines follows,each lines contains two integer L,R(1<=L<=R<=n),denote a query.

 

Output

For each case, first you should print "Case #x:", where x indicates the case number between 1 and T.
Then for each query print the answer in one line.

 

Sample Input

1

5

3 2 5 4 1

3

1 5

2 4

3 3

 

Sample Output

Case #1:

11

4

0

 

Source

2013 Multi-University Training Contest 8

题意概括：

给出 1~N 的一个排列，M次查询，每次查询 L ~ R 内 GCD( ai, aj )  [ L <= i < j <= R ] 的总和。

解题思路：

又是涉及 GCD 又是 涉及区间查询，头有点大。

首先莫队处理区间查询，其次欧拉函数解决GCD问题。

根据：

那么用 gcd( ai, aj) 代替上式的 n，我们可以得到：

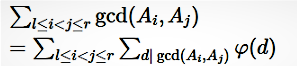
问题就转换成了求 d 的欧拉函数，其实 d 是有很多重复的，那么我们只要统计出当前查询区间【L，R】内 d 出现的次数然后乘上其欧拉函数值，所求的的答案就是区间GCD的总和。

欧拉函数值和对原序列的每一项的因数分解预处理时搞定。

AC code：

 #include <cstdio>
 #include <iostream>
 #include <algorithm>
 #include <cstring>
 #include <vector>
 #include <cmath>
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;

 const int MAXN = 2e4+;
 int unit, a[MAXN], N, M, cnt[MAXN];
 LL ans[MAXN], phi[MAXN];
 vector<int>factor[MAXN];

 struct Query
 {
     int l, r, idx;
     friend bool operator < (const Query & a, const Query & b){
         int x1 = a.l/unit, x2 = b.l/unit;
         if(x1 != x2) return x1 < x2;
         return a.r < b.r;
     }
 }Q[MAXN];

 void init()
 {
     for(int i = ; i < MAXN; i++){      //分解因子
         for(int j = i; j < MAXN; j+=i)
             factor[j].push_back(i);
     }

     phi[] = ;                         //欧拉函数
     for(int i = ; i < MAXN; i++){
         phi[i] = i;
     }
     for(int i = ; i < MAXN; i++){
         if(phi[i] == i){
             for(int j = i; j < MAXN; j+=i)
                 phi[j] = phi[j]/i*(i-);
         }
         //puts("zjy");
     }
 }

 LL add(int x)
 {
     LL res = ;
     for(auto d : factor[x]) res+=cnt[d]*phi[d];
     for(auto d : factor[x]) cnt[d]++;
     return res;
 }

 LL del(int x)
 {
     LL res = ;
     for(auto d : factor[x]) cnt[d]--;
     for(auto d : factor[x]) res+=cnt[d]*phi[d];
     return -res;
 }

 void solve()
 {
     memset(cnt, , sizeof(cnt));
     int L = , R = ;
     LL cur = ;
     for(int i = ; i <= M; i++){
         while( L < Q[i].l) cur += del(a[L++]);
         while( L > Q[i].l) cur += add(a[--L]);
         while( R < Q[i].r) cur += add(a[++R]);
         while( R > Q[i].r) cur += del(a[R--]);
         ans[Q[i].idx] = cur;
         //puts("zjy");
     }
 }

 int main()
 {
     int T_Case, Cas = ;
     init();
     //puts("zjy");
     scanf("%d", &T_Case);
     while(T_Case--){
         scanf("%d", &N);
         for(int i = ; i <= N; i++) scanf("%d", &a[i]);
         scanf("%d", &M);
         for(int i = ; i <= M; i++){
             scanf("%d %d", &Q[i].l, &Q[i].r);
             Q[i].idx = i;
         }
         unit = sqrt(N);
         sort(Q+, Q++M);
         solve();
         printf("Case #%d:\n", ++Cas);
         for(int i = ; i <= M; i++) printf("%lld\n", ans[i]);
     }
     return ;
 }