Bellman-Ford算法——解决负权边

Dijkstra算法虽然好，但是它不能解决带有负权边（边的权值为负数）的图。

接下来学习一种无论在思想上还是在代码实现上都可以称为完美的最短路径算法：Bellman-Ford算法。

Bellman-Ford算法非常简单，核心代码四行，可以完美的解决带有负权边的图。

for(k=;k<=n-;k++)  //外循环循环n-1次，n为顶点个数
    for(i=;i<=m;i++)//内循环循环m次，m为边的个数，即枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
            dis[v[i]]=dis[u[i]]+w[i]; 

在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1条边，最短路径中不可能包含回路。

　　因为最短路径是一个不包含回路的简单路径，回路分为正权回路(回路权值之和为正)和负权回路(回路权值之和为负)。如果最短路径中包含正权回路，那么去掉这个回路，一定可以得到更短的路径；如果最短路径中包含负权回路，那么肯定没有最短路径，因为每多走一次负权回路就可以得到更短的路径. 因此最短路径肯定是一个不包含回路的最短路径，即最多包含n-1条边。

Bellman-Ford算法的主要思想：

　　首先dis数组初始化顶点u到其余各个顶点的距离为∞，dis[u] = 0。

　　然后每轮对输入的所有边进行松弛，更新dis数组，至多需要进行n-1次就可以求出顶点u到其余各顶点的最短路径（因为任意两点之间的最短路径最多包含n-1条边，所以只需要n-1轮就行）。

一句话概括Bellman-Ford算法就是：对所有边进行n-1次“松弛”操作。

此外，Bellman-Ford算法可以检测一个图是否有负权回路。如果已经进行了n-1轮松弛之后，仍然存在

if(dis[v[i]]>dis[u[i]]+w[i])
    dis[v[i]]=dis[u[i]]+w[i];

的情况，也就是说在进行n-1轮之后，仍然可以继续成功松弛，那么这个图一定存在负权回路。

关键代码如下：

//Bellman-Ford算法核心语句
for(k=;k<=n-;k++)  //外循环循环n-1次，n为顶点个数
    for(i=;i<=m;i++)//内循环循环m次，m为边的个数，即枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
            dis[v[i]]=dis[u[i]]+w[i];
//检测负权回路
flag=;
for(i=;i<=m;i++)
    if(dis[v[i]]>dis[u[i]]+w[i])
        flag=;
if(flag==)
    printf("此图有负权回路");

显然，算法复杂度为O（NM），比Dijkstra算法还高，当然可以进行优化。

在实际操作中，Bellman-Ford算法经常会在没有达到n-1轮松弛前就已经计算出最短路，上面已经说过，n-1其实是最大轮回次数。

因此可以添加一个变量check用来标记数组dis在本轮松弛中是否发生了变化，若没有变化，则提前跳出循环。

完整代码如下：

#include <stdio.h>

#define INF 999999
int main()
{
    int i, j, n, m;
    int dis[], bak[], u[], v[], w[];
    int check, flag = ;
    //读入n和m，n表示顶点个数，m表示边的条数
    scanf_s("%d %d", &n, &m);
    //读入边
    for (i = ; i <= m; ++i)
    {
        scanf_s("%d %d %d", &u[i], &v[i], &w[i]);
    }
    //初始化dis数组，这里是1号顶点到其余顶点的初始路程
    for (i = ; i <= n; ++i)
    {
        dis[i] = INF;
    }
    dis[] = ;

    // Bellman-Ford算法核心代码
    for (j = ; j <= n-; ++j)     //最多循环n-1轮
    {
        check = ;//用来标记在本轮松弛中数组dis是否发生更新
        for (i = ; i <= m; ++i)        // 最核心的3句Bellman-Ford算法
        {
            if (dis[v[i]] > dis[u[i]] + w[i])
            {
                dis[v[i]] = dis[u[i]] + w[i];
                check = ;//数组dis发生更新，改变check的值
            }
        }
        //松弛完毕后检测数组dis是否有更新
        if (check==)
        {
            break; //没有更新则提前退出程序
        }
    }

    //检测负权回路
    for (i = ; i <= m; ++i)     // n-1次之后最短路径还会发生变化则含有负权回路
    {
        if (dis[v[i]] > dis[u[i]] + w[i])
        {
            flag = ;
        }
    }

    if (flag==)
    {
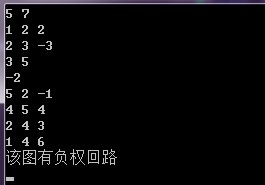
        printf("该图有负权回路");
    }
    else
    {
        //输出最终结果
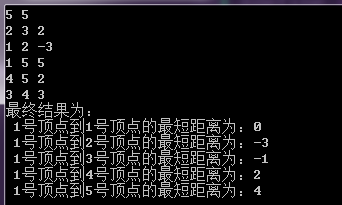
        printf("最终结果为：\n");
        for (i = ; i <= n; ++i)
        {
            printf(" 1号顶点到%d号顶点的最短距离为：%d\n", i,dis[i]);
        }
    }
    printf("\n");
    getchar();
    getchar();
    return ;
}